% 例題A3.1.6：オイラー線 （One More）★★★
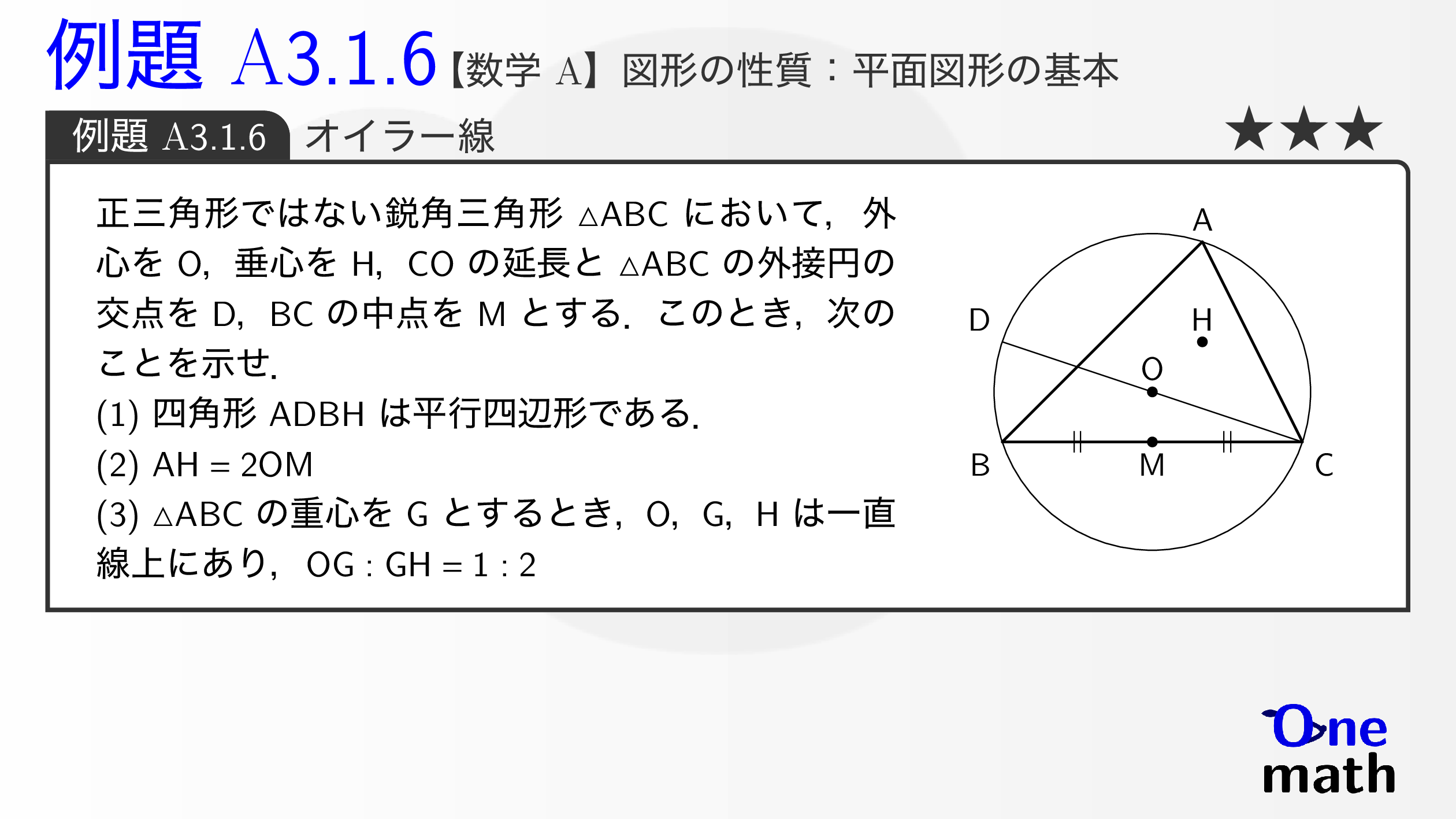
正三角形ではない鋭角三角形の$\triangle \mathrm{ABC}$において,外心を$\mathrm{O}$,垂心を$\mathrm{H}$,$\mathrm{CO}$の延長と$\triangle \mathrm{ABC}$の外接円の交点を$\mathrm{D}$,$\mathrm{BC}$の中点を$\mathrm{M}$とする.このとき,次のことを示せ. (1)四角形ADBHは平行四辺形である. (2)$\mathrm{AH}=2 \mathrm{OM}$(3)$\triangle \mathrm{ABC}$の重心を$\mathrm{G}$とするとき,$\mathrm{O}$,$\mathrm{G}$,$\mathrm{H}$は一直線上にあり,$\mathrm{OG}: \mathrm{GH}=1: 2$
% 解答（例題A3.1.6）
(1)CDは$\triangle \mathrm{ABC}$の外接円の直径であるから,$$\mathrm{DB} \perp \mathrm{BC}$$Hは$\triangle \mathrm{ABC}$の垂心であるから,$$\mathrm{AH} \perp \mathrm{BC}$$したがって,$\mathrm{DB}\parallel \mathrm{AH} \cdots (\mathrm{i})$同様に,$\mathrm{DA} \perp \mathrm{AC},\mathrm{BH} \perp \mathrm{AC}$より,$\mathrm{DA}\parallel \mathrm{BH} \cdots (\mathrm{ii})$よって,(i),(ii)より,四角形ADBHは平行四辺形である.$\blacksquare$(2)(1)より,四角形ADBHは平行四辺形であるから,$\mathrm{AH}=\mathrm{DB} \cdots (\mathrm{iii})$$\mathrm{OM} \perp \mathrm{BC}$より,$\mathrm{DB} \parallel \mathrm{OM}$であり,$\mathrm{O}$,$\mathrm{M}$はそれぞれ$\mathrm{CD}$,$\mathrm{BC}$の中点であるから,$\mathrm{DB}=2 \mathrm{OM} \cdots (\mathrm{iv})$よって,(iii),(iv)より,$\mathrm{AH}=2 \mathrm{OM} \blacksquare$(3)$\mathrm{OH}$と$\mathrm{AM}$の交点を$\mathrm{G}^{\prime}$とする. (1),(2)より,$\mathrm{OM} \parallel \mathrm{AH}$であるから,$$\mathrm{AG}^{\prime}: \mathrm{G}^{\prime} \mathrm{M}=\mathrm{AH}: \mathrm{OM}=2: 1$$したがって,$\mathrm{G}^{\prime}$は$\triangle \mathrm{ABC}$の重心$\mathrm{G}$と一致する. よって,$\mathrm{O}$,$\mathrm{G}$,$\mathrm{H}$は一直線上にあり,$$\mathrm{OG}: \mathrm{GH}=\mathrm{OM}: \mathrm{AH}=1: 2 \blacksquare$$
% 問題A3.1.6
$\triangle \mathrm{ABC}$の垂心を$\mathrm{H}$とし,辺$\mathrm{BC}$,$\mathrm{CA}$,$\mathrm{AB}$の中点をそれぞれ$\mathrm{D}$,$\mathrm{E}$,$\mathrm{F}$とする.$\triangle \mathrm{DEF}$の垂心を$\mathrm{O}$とするとき,$\mathrm{AD}$と$\mathrm{OH}$の交点$\mathrm{G}$が,$\triangle \mathrm{ABC}$の重心であることを示せ.
% 解答A3.1.6
$\mathrm{O}$は$\triangle \mathrm{DEF}$の垂心であるから,$\mathrm{OD} \perp \mathrm{EF}$$\mathrm{E}$,$\mathrm{F}$はそれぞれ辺$\mathrm{CA}$$\mathrm{AB}$の中点であるから,中点連結定理より,$$\mathrm{EF} \parallel \mathrm{BC}$$したがって,$\mathrm{OD} \perp \mathrm{BC} \cdots (\mathrm{i})$また,$\mathrm{H}$は$\triangle \mathrm{ABC}$の垂心であるから,$\mathrm{AH} \perp \mathrm{BC} \cdots (\mathrm{ii})$(i),(ii)より,$\mathrm{OD} \parallel \mathrm{AH}$$\triangle \mathrm{ABC} \backsim \triangle \mathrm{DEF}$であるから,$\mathrm{AH}:\mathrm{OD}=2:1$$\mathrm{OD} \parallel \mathrm{AH}$より,$\mathrm{AG}:\mathrm{DG}=\mathrm{AH}:\mathrm{OD}=2:1$よって,$\mathrm{G}$は$\triangle \mathrm{ABC}$の中線$\mathrm{AD}$を$2:1$に内分する点であるから,点$\mathrm{G}$は$\triangle \mathrm{ABC}$の重心である.$\blacksquare$
