問題の解答
検索用コード(LaTeX)
% 例題A3.2.7:共通接線 (One More)★★★
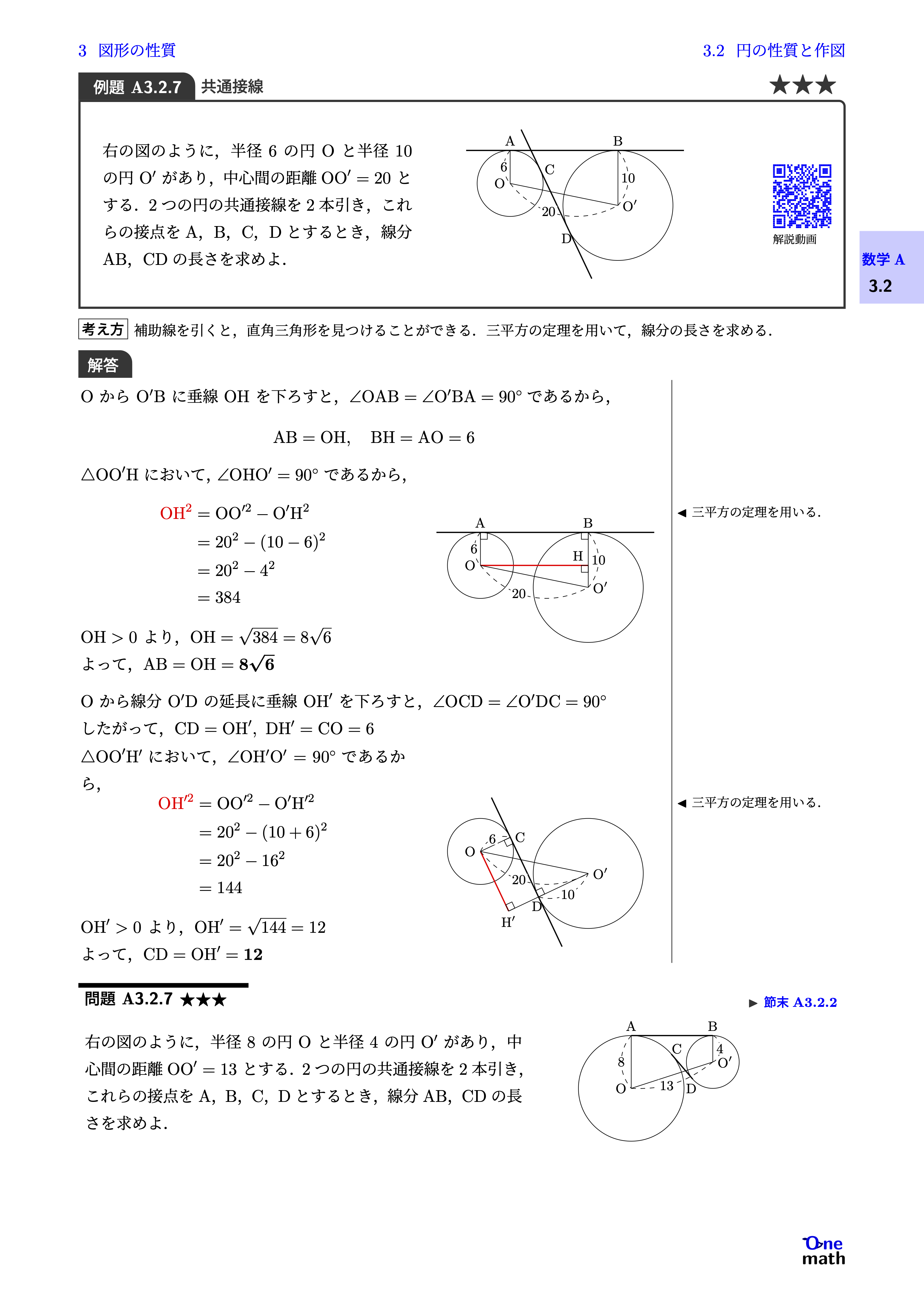
右の図のように,半径6の円Oと半径10の円$\mathrm{O}^{\prime}$があり,中心間の距離$\mathrm{OO}^{\prime}=20$とする.2つの円の共通接線を2本引き,これらの接点をA,B,C,Dとするとき,線分AB,CDの長さを求めよ.
% 解答(例題A3.2.7)
Oから$\mathrm{O}^{\prime}$Bに垂線OHを下ろすと,$\angle \mathrm{OAB}=\angle \mathrm{O^\prime BA}=90^\circ$であるから,$$\mathrm{AB}=\mathrm{OH},\mathrm{BH}=\mathrm{AO}=6$$$\triangle \mathrm{OO}^{\prime} \mathrm{H}$において,$\angle \mathrm{OHO^\prime}=90^{\circ}$であるから,$$\begin{aligned} \mathrm{OH^2} &=\mathrm{OO}^{\prime 2}-\mathrm{O}^{\prime} \mathrm{H}^2 \\ &=20^2-(10-6)^2\\ &=20^2-4^2 \\ &=384 \end{aligned}$$$\mathrm{OH}>0$より,$\mathrm{OH}=\sqrt{384}=8\sqrt{6}$よって,$\mathrm{AB}=\mathrm{OH}=8\sqrt{6}$Oから線分$\mathrm{O}^{\prime} \mathrm{D}$の延長に垂線$\mathrm{OH}^{\prime}$を下ろすと,$\angle \mathrm{OCD}=\angle \mathrm{O^\prime DC}=90^{\circ}$したがって,$\mathrm{CD}=\mathrm{OH}^{\prime},\mathrm{DH}^{\prime}=\mathrm{CO}=6$$\triangle \mathrm{OO}^{\prime} \mathrm{H}^{\prime}$において,$\angle \mathrm{OH^{\prime}O^\prime}=90^{\circ}$であるから,$$\begin{aligned} \mathrm{OH^{\prime 2}}&=\mathrm{OO}^{\prime 2}-\mathrm{O}^{\prime} \mathrm{H}^{\prime 2} \\ &=20^2-(10+6)^2\\ &=20^2-16^2 \\ &=144 \end{aligned}$$$\mathrm{OH}^{\prime}>0$より,$\mathrm{OH}^{\prime}=\sqrt{144}=12$よって,$\mathrm{CD}=\mathrm{OH}^{\prime}=12$
% 問題A3.2.7
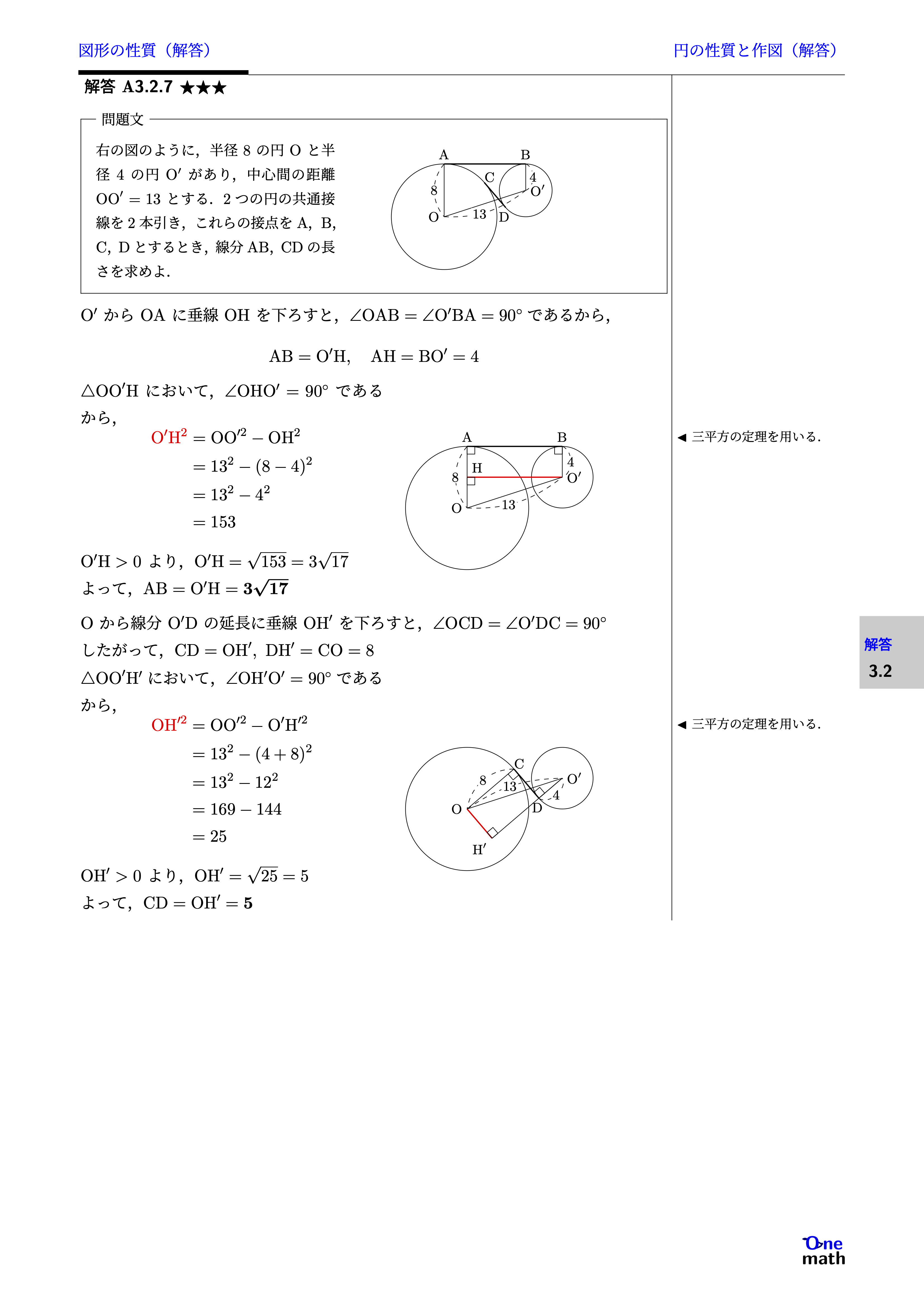
右の図のように,半径8の円Oと半径4の円$\mathrm{O}^{\prime}$があり,中心間の距離$\mathrm{OO}^{\prime}=13$とする.2つの円の共通接線を2本引き,これらの接点をA,B,C,Dとするとき,線分AB,CDの長さを求めよ.
% 解答A3.2.7
$\mathrm{O}^{\prime}$からOAに垂線OHを下ろすと,$\angle \mathrm{OAB}=\angle \mathrm{O^\prime BA}=90^\circ$であるから,$$\mathrm{AB}=\mathrm{O}^{\prime}\mathrm{H},\mathrm{AH}=\mathrm{B}\mathrm{O}^{\prime}=4$$$\triangle \mathrm{OO}^{\prime} \mathrm{H}$において,$\angle \mathrm{OHO^\prime}=90^{\circ}$であるから,$$\begin{aligned} \mathrm{O^{\prime}\mathrm{H}^2} &=\mathrm{OO}^{\prime 2}-\mathrm{O}\mathrm{H}^2 \\ &=13^2-(8-4)^2\\ &=13^2-4^2 \\ &=153 \end{aligned}$$$\mathrm{O}^{\prime}\mathrm{H}>0$より,$\mathrm{O}^{\prime}\mathrm{H}=\sqrt{153}=3\sqrt{17}$よって,$\mathrm{AB}=\mathrm{O}^{\prime}\mathrm{H}=3\sqrt{17}$Oから線分$\mathrm{O}^{\prime} \mathrm{D}$の延長に垂線$\mathrm{OH}^{\prime}$を下ろすと,$\angle \mathrm{OCD}=\angle \mathrm{O^\prime DC}=90^{\circ}$したがって,$\mathrm{CD}=\mathrm{OH}^{\prime},\mathrm{DH}^{\prime}=\mathrm{CO}=8$$\triangle \mathrm{OO}^{\prime} \mathrm{H}^{\prime}$において,$\angle \mathrm{OH^{\prime}O^\prime}=90^{\circ}$であるから,$$\begin{aligned} \mathrm{OH^{\prime 2}}&=\mathrm{OO}^{\prime 2}-\mathrm{O}^{\prime} \mathrm{H}^{\prime 2} \\ &=13^2-(4+8)^2\\ &=13^2-12^2 \\ &=169-144 \\ &=25 \end{aligned}$$$\mathrm{OH}^{\prime}>0$より,$\mathrm{OH}^{\prime}=\sqrt{25}=5$よって,$\mathrm{CD}=\mathrm{OH}^{\prime}=5$
あわせて読みたい


【数学A】3章:図形の性質(基本事項)
検索用コード(LaTeX) % 基本事項A3.1.1:角(One More) (1)対頂角の性質 対頂角が等しい.$\left(\alpha=\alpha^{\prime}\right)$ (2)平行線と同位角・錯角の性質 $$ ...
あわせて読みたい


【数学A】3章:図形の性質(節末問題・章末問題)
リンク(関連例題) https://onemath.net/onemorea-reidai3-1-6 https://onemath.net/onemorea-reidai3-1-7 https://onemath.net/onemorea-reidai3-1-9 https://onemath...
