【数学A】例題3.3.4：多面体の切断・体積（One More）★★★

% 例題A3.3.4：多面体の切断・体積 （One More）★★★
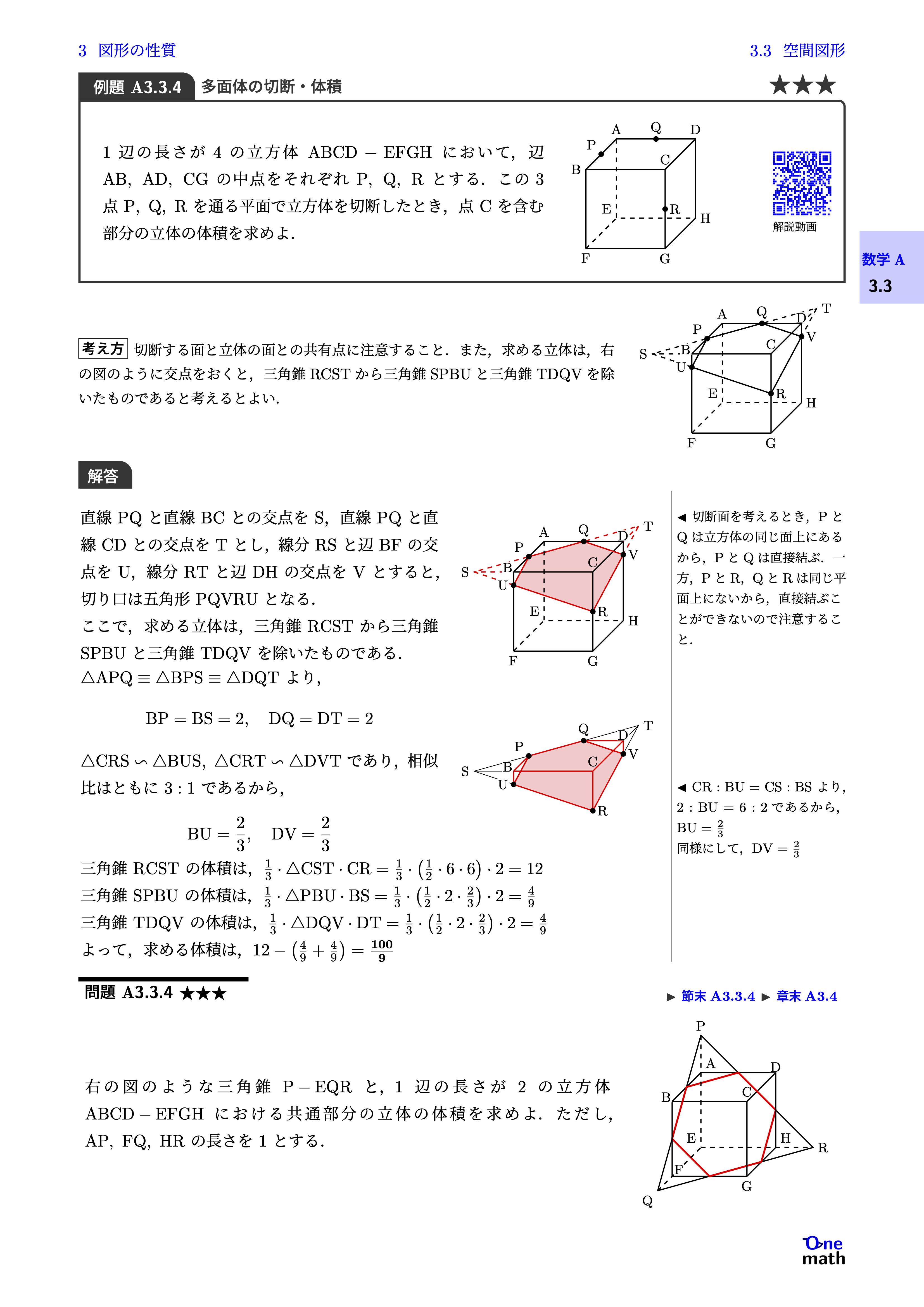
1辺の長さが4の立方体$\mathrm{ABCD}-\mathrm{EFGH}$において,辺$\mathrm{AB},\mathrm{AD},\mathrm{CG}$の中点をそれぞれ$\mathrm{P},\mathrm{Q},\mathrm{R}$とする.この3点$\mathrm{P},\mathrm{Q},\mathrm{R}$を通る平面で立方体を切断したとき,点$\mathrm{C}$を含む部分の立体の体積を求めよ.

% 解答（例題A3.3.4）
直線$\mathrm{PQ}$と直線$\mathrm{BC}$との交点を$\mathrm{S}$,直線$\mathrm{PQ}$と直線$\mathrm{CD}$との交点を$\mathrm{T}$とし,線分$\mathrm{RS}$と辺$\mathrm{BF}$の交点を$\mathrm{U}$,線分$\mathrm{RT}$と辺$\mathrm{DH}$の交点を$\mathrm{V}$とすると,切り口は五角形$\mathrm{PQVRU}$となる. ここで,求める立体は,三角錐$\mathrm{RCST}$から三角錐$\mathrm{SPBU}$と三角錐$\mathrm{TDQV}$を除いたものである.$\triangle \mathrm{APQ} \equiv \triangle \mathrm{BPS} \equiv \triangle \mathrm{DQT}$より,$$\mathrm{BP}=\mathrm{BS}=2,\mathrm{DQ}=\mathrm{DT}=2$$$\triangle \mathrm{CRS} \backsim \triangle \mathrm{BUS},\triangle \mathrm{CRT} \backsim \triangle \mathrm{DVT}$であり,相似比はともに$3: 1$であるから,$$\mathrm{BU}=\frac{2}{3},\mathrm{DV}=\frac{2}{3}$$三角錐$\mathrm{RCST}$の体積は,$\frac{1}{3} \cdot \triangle \mathrm{CST} \cdot \mathrm{CR}=\frac{1}{3} \cdot \left(\frac{1}{2} \cdot 6 \cdot 6\right) \cdot 2=12$三角錐$\mathrm{SPBU}$の体積は,$\frac{1}{3} \cdot \triangle \mathrm{PBU} \cdot \mathrm{BS}=\frac{1}{3} \cdot \left(\frac{1}{2} \cdot 2 \cdot \frac{2}{3}\right) \cdot 2=\frac{4}{9}$三角錐$\mathrm{TDQV}$の体積は,$\frac{1}{3} \cdot \triangle \mathrm{DQV} \cdot \mathrm{DT}=\frac{1}{3} \cdot \left(\frac{1}{2} \cdot 2 \cdot \frac{2}{3}\right) \cdot 2=\frac{4}{9}$よって,求める体積は,$12-\left(\frac{4}{9}+\frac{4}{9}\right)=\frac{100}{9}$

% 問題A3.3.4
右の図のような三角錐$\mathrm{P-EQR}$と,1辺の長さが2の立方体$\mathrm{ABCD-EFGH}$における共通部分の立体の体積を求めよ.ただし,$\mathrm{AP},\mathrm{FQ},\mathrm{HR}$の長さを1とする.

% 解答A3.3.4
求める立体は,三角錐$\mathrm{P-EQR}$から立方体に重なっていない部分の3つの三角錐の体積を除いたものである. 三角錐$\mathrm{P-EQR}$の体積を$V$とすると,$$V=\frac{1}{3} \cdot \triangle \mathrm{EQR} \cdot \mathrm{EP}=\frac{1}{3} \times \left\{\frac{1}{2} \times(2+1)\times(2+1)\right\} \times(2+1) =\frac{9}{2}$$三角錐$\mathrm{P-EQR}$において,立方体に重なっていない部分の3つの三角錐の体積は,$$\mathrm{AP} : \mathrm{EP}=\mathrm{FQ} : \mathrm{EQ}=\mathrm{HR} : \mathrm{ER}=1 : 3$$より,それぞれ$\frac{1}{27} V$である. よって,求める体積は,$V-3 \times\frac{1}{27} V=\frac{8}{9} V=4$