問題の解答
検索用コード（LaTeX）
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 例題I1.3.3：1次不等式，連立1次不等式（One More）★
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
次の不等式，連立1次不等式を解け．
(1) $\{\begin{array}{l}5x+4>3x+2\\-x+4\geqq 2(x-1)\end{array}$
(2) $\{\begin{array}{l}x+5<-1-2x\\3x+1\geqq 1\end{array}$
(3) $x+1<2x+3<5x$
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 例題I1.3.3の解答（One More）★
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
(1) $5x+4>3x+2$より，$2x>-2$
したがって，$x>-1\cdots(\mathrm{i})$
また，$-x+4\geqq 2(x-1)$より，$-3x\geqq-6$
したがって，$x\leqq 2\cdots(\mathrm{ii})$
よって，(i)と(ii)の共通範囲を求めると，
\[
-1<x\leqq 2
\]
(2) $x+5<-1-2x$より，$3x<-6$
したがって，$x<-2\cdots(\mathrm{i})$
また，$3x+1\geqq 1$より，$3x\geqq 0$
したがって，$x\geqq 0\cdots(\mathrm{ii})$
(i)と(ii)の共通範囲はない．
よって，解なし
(3) $x+1<2x+3<5x$より，$\{\begin{array}{l}x+1<2x+3\\2x+3<5x\end{array}$
$x+1<2x+3$より，$-x<2$
したがって，$x>-2\cdots(\mathrm{i})$
また，$2x+3<5x$より，$-3x<-3$
したがって，$x>1\cdots(\mathrm{ii})$
よって，(i)と(ii)の共通範囲を求めると，$x>1$
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 問題I1.3.3：1次不等式，連立1次不等式（One More）★
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
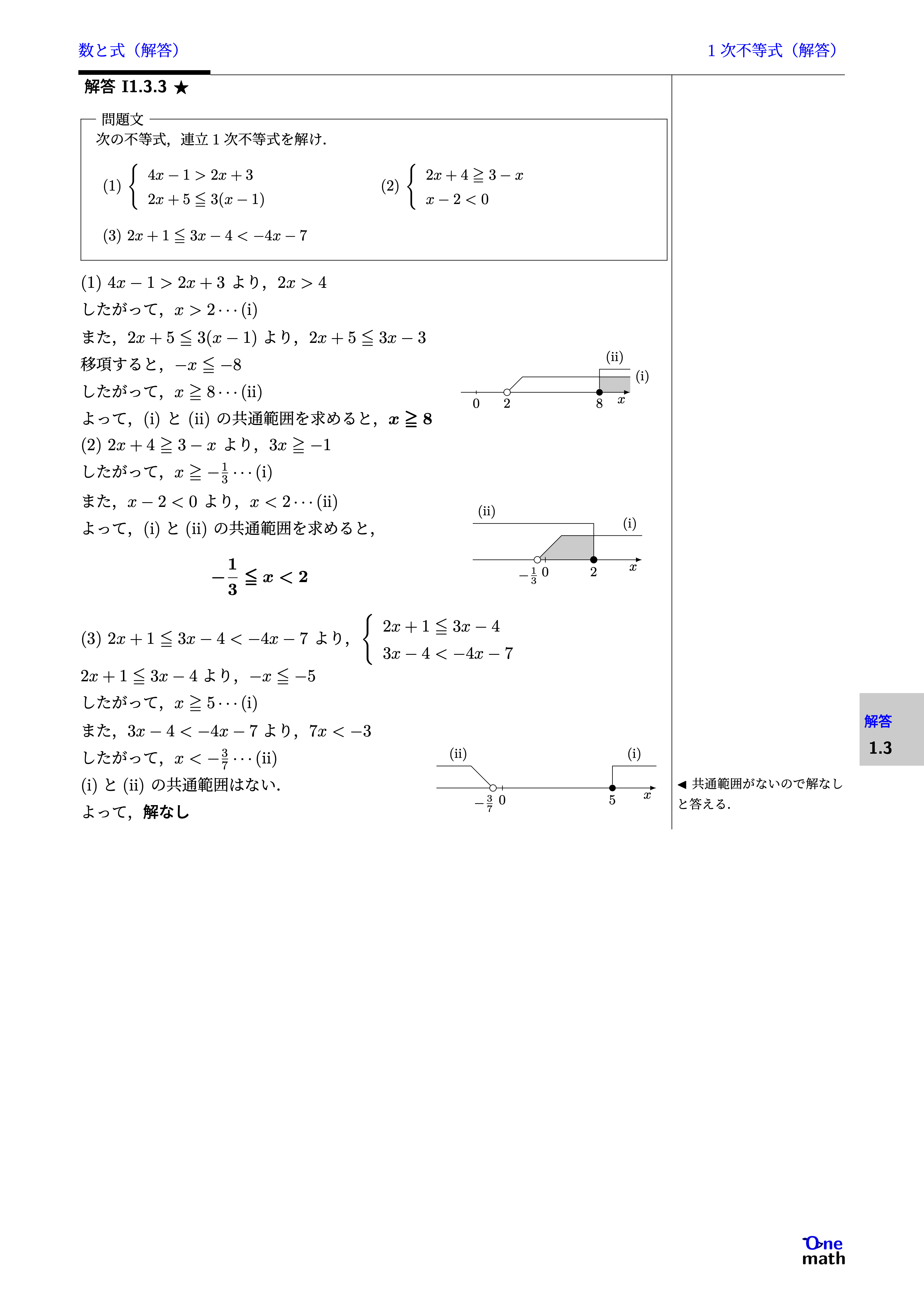
次の不等式，連立1次不等式を解け．
(1) $\{\begin{array}{l}4x-1>2x+3\\2x+5\leqq 3(x-1)\end{array}$
(2) $\{\begin{array}{l}2x+4\geqq 3-x\\x-2<0\end{array}$
(3) $2x+1\leqq 3x-4<-4x-7$
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 問題I1.3.3の解答（One More）★
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
(1) $4x-1>2x+3$より，$2x>4$
したがって，$x>2\cdots(\mathrm{i})$
また，$2x+5\leqq 3(x-1)$より，$2x+5\leqq 3x-3$
移項すると，$-x\leqq-8$
したがって，$x\geqq 8\cdots(\mathrm{ii})$
よって，(i)と(ii)の共通範囲を求めると，$x\geqq 8$
(2) $2x+4\geqq 3-x$より，$3x\geqq-1$
したがって，$x\geqq-\frac{1}{3}\cdots(\mathrm{i})$
また，$x-2<0$より，$x<2\cdots(\mathrm{ii})$
よって，(i)と(ii)の共通範囲を求めると，
\[
-\frac{1}{3}\leqq x<2
\]
(3) $2x+1\leqq 3x-4<-4x-7$より，$\{\begin{array}{l}2x+1\leqq 3x-4\\3x-4<-4x-7\end{array}$
$2x+1\leqq 3x-4$より，$-x\leqq-5$
したがって，$x\geqq 5\cdots(\mathrm{i})$
また，$3x-4<-4x-7$より，$7x<-3$
したがって，$x<-\frac{3}{7}\cdots(\mathrm{ii})$
(i)と(ii)の共通範囲はない．
よって，解なし
あわせて読みたい
【数学I】1章：数と式（基本事項）
検索用コード（LaTeX） 本文・解答側注 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 基本事項I1.1.1：単項式と多項式（One More） %%%%%%%%%%%%%%%%%%%%%%%%...
あわせて読みたい
【数学I】1章：数と式（節末問題・章末問題）
節末I1.1.1〜I1.1.5の解答 節末I1.1.1節末I1.1.2節末I1.1.3節末I1.1.4節末I1.1.5 リンク（関連例題） https://onemath.net/onemorei-reidai1-1-1 https://onemath.net/o...