% 基本事項I2.1.1:集合(One More)
(1)明確な範囲をもつ事物の集まりを集合という.また,集合に属する1つ1つのものを,その集合の要素という.ある要素$a$が集合$A$に含まれる場合,$a$は集合$A$に属するといい,$a \in A$と表す.逆に,要素$b$が集合$A$に含まれない場合には,$b \notin A$と表す.このとき,任意の要素$a$と集合$A$の関係において,$a \in A$または$a \notin A$のいずれかが成り立つ.要素が有限個である集合を有限集合,要素の数が無限に存在する集合を無限集合という. (2)集合を表すには,次の2つの方法がある. (i)要素を列記する方法 (ii)要素の満たす条件を述べて表す方法 例えば,1桁の正の奇数の集合を$A$とすると,$A$には次のような表し方がある. (i)$A=\{1, 3, 5, 7, 9\}$ (ii)$A=\{x \mid 1 \leqq x \leqq 9, x$は奇数$\}$,$A=\{2 n-1 \mid 1 \leqq n \leqq 5, n$は整数$\}$ (3)2つの集合$A, B$に関して,$A$のすべての要素が$B$の要素でもある場合,つまり$x \in A$ならば$x \in B$が成り立つとき,$A$を$B$の部分集合といい,$A \subset B$と表す.このとき,$A$は$B$に含まれる,あるいは$B$は$A$を含むという.また,$A$は$A$自身の部分集合でもあり,任意の集合$A$について$A \subset A$が成り立つ. 2つの集合$A, B$が一致しているとは,互いに他方の部分集合となっていることである.すなわち, $A \text{ と } B \text{ が等しい } \Longleftrightarrow A \subset B \text{ かつ } B \subset A \Longleftrightarrow A=B$ (4)空集合$\varnothing$は,要素を1つも含まない集合を指す.任意の集合$A$に対して,$\varnothing$は$A$の部分集合であるとする.すなわち,$\varnothing \subset A$と約束する. $A, B$の両方に属するような要素全体の集合を$A$と$B$ の共通部分($A$と$B$の交わ り)といい,$A \cap B$で表す. $A, B$の少なくとも一方に属するような要素全体の集合を$A$と$B$の和集合($A$と$B$の結び)といい,$A \cup B$で表す. (5)全体集合とは,特定の文脈や議論において,考えられるすべての要素を含む集合である. 補集合とは,全体集合$U$に属し,かつ$U$の部分集合$A$に属さない要素全体からなる集合である.これを$\overline{A}$で表す($A^c$で表されることもある) また,次のことが成り立つ. $$\overline{\varnothing}=U, \overline{U}=\varnothing, A \cap \overline{A}=\varnothing, A \cup \overline{A}=U, \overline{\overline{A}}=A$$ (6)ド・モルガンの法則(ド・モーガンの法則) $\overline{A \cup B}=\overline{A} \cap \overline{B}$ $\overline{A \cap B}=\overline{A} \cup \overline{B}$
% 基本事項I2.1.2:命題(One More)
(1)式や文章によって示される事柄で,明確に正しいか正しくないかが決定される文や式を命題という.命題が正しい場合,その命題は真であるといい,正しくない場合は偽であるという.命題においては,真または偽のいずれかが必ず確定する. (2)文字を含んだ文や式において,文字のとる値を変えると,真偽が変わるものがある.例えば,$x+y=11$は,$x=1, y=10$のときは真,$x=2, y=3$のときは偽である. このように,含まれる文字に値を代入することで真偽が明確に決まる(すなわち,命題となる)文や式を条件という.また,これを「$x$と$y$に関する条件」などということもある. (3)命題「$p \Longrightarrow q$」において,条件$p$を満たす要素の集合を$P$,条件$q$を満たす要素の集合を$Q$とする. $$ \begin{aligned} &\text{「} p \Longrightarrow q \text { が真 }\text{」}\Longleftrightarrow P \subset Q \Longleftrightarrow P \cap \overline{Q}=\varnothing, \\ &\text{「} p \Longleftrightarrow q \text{ が真 }\text{」}\Longleftrightarrow P=Q \end{aligned} $$ (4)命題「$p \Longrightarrow q$」において,$p$は満たすが$q$を満たさないような例を反例という.反例が1つでもあれば,命題「$p \Longrightarrow q$」は偽であるといえる. $p \Longrightarrow q$が偽
% 基本事項I2.1.3:必要条件と十分条件(One More)
命題「$p \Longrightarrow q$」が真の場合, $p$は$q$であるための十分条件である, $q$は$p$であるための必要条件であるという. 命題「$p \Longrightarrow q$」と「$q \Longrightarrow p$」が共に真である,すなわち,命題「$p \Longleftrightarrow q$」が成り立つとき, $p$は$q$($q$は$p$)であるための必要十分条件であるという. また,この場合,$p$と$q$は互いに同値であるという.
% 基本事項I2.1.4:条件の否定(One More)
(1)条件$p, q$を満たすもの全体の集合をそれぞれ$P, Q$とする. このとき,$p$と$q$をともに満たすものの全体の集合は$P\cap Q$,$p$または$q$のいずれかを満たすものの全体の集合は$P\cup Q$である. (2)条件$p$の否定($p$ではない)を$\overline{p}$で表す.$\overline{p}$を満たすものの集合は,$p$を満たすものの集合$P$の補集合$\overline{P}$となる. (3)ド・モルガンの法則 $$\overline{p \text{かつ} q}\Longleftrightarrow \overline{p} \text{または} \overline{q}, \overline{p \text {または} q}\Longleftrightarrow \overline{p} \text{かつ} \overline{q}$$ (4)「すべて」と「ある」の否定は次のようになる. 命題「すべての$x$について$p$である」の否定は,「ある$x$について$\overline{p}$である」 命題「ある$x$について$p$である」の否定は,「すべての$x$について$\overline{p}$である」
% 基本事項I2.1.5:逆・裏・対偶(One More)
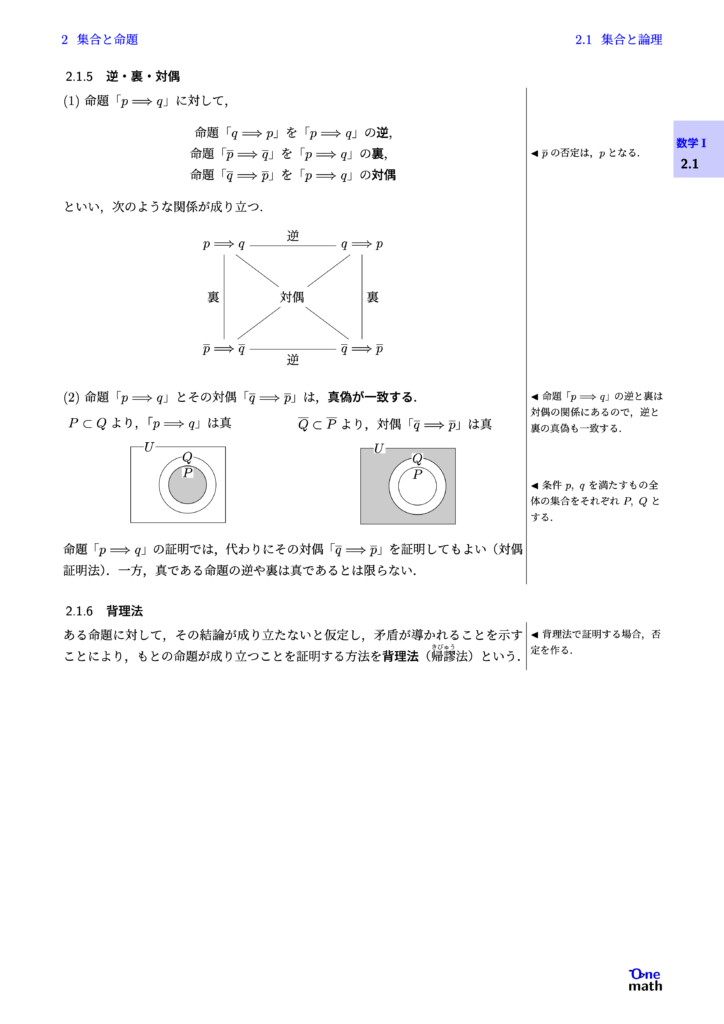
(1)命題「$p \Longrightarrow q$」に対して, 命題「$q \Longrightarrow p $」を「$p \Longrightarrow q$」の逆, 命題「$\overline{p} \Longrightarrow \overline{q}$」を「$ p \Longrightarrow q$」の裏, 命題「$\overline{q} \Longrightarrow \overline{p}$」を「$p \Longrightarrow q$」の対偶 といい,次のような関係が成り立つ. (2)命題「$ p \Longrightarrow q$」とその対偶「$\overline{q} \Longrightarrow \overline{p}$」は,真偽が一致する. $P \subset Q $より, 「$p \Longrightarrow q$」は真 $\overline{Q} \subset \overline{P} $より, 対偶「$\overline{q} \Longrightarrow \overline{p}$」は真 命題「$ p \Longrightarrow q $」の証明では,代わりにその対偶「$ \overline{q} \Longrightarrow \overline{p} $」を証明してもよい(対偶証明法). 一方,真である命題の逆や裏は真であるとは限らない.
% 基本事項I2.1.6:背理法(One More)
ある命題に対して,その結論が成り立たないと仮定し,矛盾が導かれることを示すことにより,もとの命題が成り立つことを証明する方法を背理法(\ruby{帰謬}{き|びゅう}法)という.