% 基本事項I3.1.1:関数(One More)
(1)2つの変数$x,y$があり,$x$の値を定めるとそれに応じて$y$の値がただ1つ定まるとき,$y$は$x$の関数であるといい,$y=f(x), y=g(x)$などと表す.また,$x$の関数を単に関数$f(x)$ともいう. (2)関数$y=f(x)$において,$x=a$のときの$y$の値を$f(a)$と表し,$f(a)$を関数$f(x)$の$x=a$における値という. (3)座標の定められた平面を座標平面という.座標軸によって分けられている4つの部分を,右の図のように,第1象限,第2象限,第3象限,第4象限という.また,座標軸上の点は,どの象限にも属さないものとする. (4)関数$y=f(x)$において,$x$のとる値の範囲をこの関数の定義域といい,$x$が定義域内のすべての値をとるときの$y$のとる値の範囲を値域という.
% 基本事項I3.1.2:2次関数$y=a(x-p)^2+q$(標準形)のグラフ(One More)
2次関数$y=a(x-p)^2+q$ のグラフは,$y=a x^2$のグラフを $x$軸方向に$p, y$軸方向に$q$だけ平行移動した放物線で, 軸は直線$x=p$, 頂点は点$(p, q)$ また,この放物線は$a>0$のときは下に凸,$a<0$のときは上に凸である.
% 基本事項I3.1.3:2次関数$y=ax^2+bx+c$(一般形)のグラフ(One More)
$y=a x^2+b x+c$の右辺を$y=a(x-p)^2+q$の形に変形することを平方完成という. $$ \begin{aligned} y &=a x^2+b x+c \\ &=a\left(x^2+\frac{b}{a} x\right)+c \\ &=a\left\{\left(x+\frac{b}{2 a}\right)^2-\left(\frac{b}{2 a}\right)^2\right\}+c \\ &=a\left(x+\frac{b}{2 a}\right)^2-a \cdot \frac{b^2}{4 a^2}+c \\ &=a\left(x+\frac{b}{2 a}\right)^2-\frac{b^2-4 a c}{4 a}\end{aligned} $$ この関数のグラフは,$y=ax^2$のグラフを平行移動した放物線で, 軸は直線$x=-\frac{b}{2 a}$,頂点は点$\left(-\frac{b}{2 a},-\frac{b^2-4 a c}{4 a}\right)$
% 基本事項I3.1.4:曲線の平行移動(One More)
関数$y=f(x)$のグラフ$F$を$x$軸方向に$p, y$軸方向に$q$だけ平行移動して得られる$F^\prime $の方程式は,次のようになる. $$y-q=f(x-p)$$ 例:$y=2x^2$のグラフを$F, y=2(x-3)^2+2$のグラフを$F^\prime$とすると,$F^\prime$は$F$を$x$軸方向に$3, y$軸方向に$2$だけ平行移動したものである.$\cdots(\mathrm{i})$ なお,ここで$F^\prime$上の点$\mathrm{P}(x,y)$をとり,(i)の平行移動によってPに移される$F$上の点を$\mathrm{Q}(X,Y)$とすると, $$x=X+3,Y=y+2$$ すなわち,$X=x-3,Y=y-2$であり,点Qは$F$上にあるから,$Y=2X^2$ この式の$X$に$x-3$,$Y$に$y-2$を代入すると,$F$の方程式は, $$y-2=2(x-3)^2$$ このように,$F^\prime$の方程式は,$F$の方程式において, $y=2x^2$の$x$を$x-3, y$を$y-2$ におき換えたものになっている.
% 基本事項I3.1.5:点・グラフの対称移動(One More)
点$(a,b)$の対称移動 (i)$x$軸に関して対称移動$\cdots $点$(a,-b)$に移る. (ii)$y$軸に関して対称移動$\cdots $点$(-a,b)$に移る. (iii)原点に関して対称移動$\cdots $点$(-a,-b)$に移る. 関数$y=f(x)$のグラフの平行移動・対称移動 (i)$x$軸方向に$p$だけ平行移動$\cdots x$を$x-p$におき換えて,$y=f(x-p)$ (ii)$y$軸方向に$q$だけ平行移動$\cdots y$を$y-q$におき換えて, $y-q=f(x)$ (iii)$x$軸方向に$p$,$y$軸方向に$q$だけ平行移動 $\cdots x$を$x-p$,$y$を$y-q$におき換えて, $ y-q=f(x-p) $ (iv)$x$軸に関して対称移動$\cdots y$を$-y$におき換えて,$-y=f(x)$ (v)$y$軸に関して対称移動$\cdots x$を$-x$におき換えて,$y=f(-x)$ (vi)原点に関して対称移動$\cdots x$を$-x$,$y$を$-y$におき換えて,$-y=f(-x)$
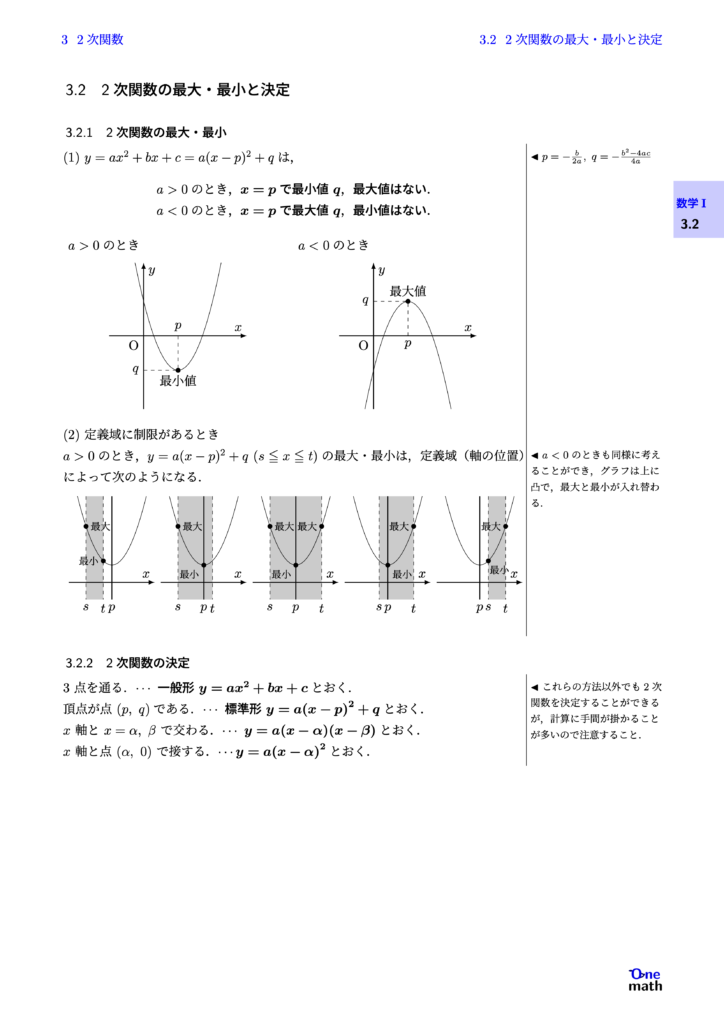
% 基本事項I3.2.1:2次関数の最大・最小(One More)
(1)$y=a x^2+b x+c=a(x-p)^2+q$は, $a>0 $のとき,$x=p$で最小値$q$,最大値はない. $a<0$のとき,$x=p$で最大値$q$,最小値はない. $a>0$のとき $a<0$のとき (2)定義域に制限があるとき $a>0$のとき,$y=a(x-p)^2+q(s \leqq x \leqq t)$の最大・最小は,定義域(軸の位置)によって次のようになる.
% 基本事項I3.2.2:2次関数の決定(One More)
3点を通る. $\cdots$一般形$y=ax^2+bx+c$とおく. 頂点が点$(p,q)$である. $\cdots$標準形$y=a(x-p)^2+q$とおく. $x$軸と$x=\alpha, \beta$で交わる.$\cdots$$y=a(x-\alpha)(x-\beta)$とおく. $x$軸と点$(\alpha, 0)$で接する.$\cdots y=a(x-\alpha)^2$とおく.
% 基本事項I3.3.1:2次方程式の解法(One More)
2次方程式$a x^2+b x+c=0\cdots(\mathrm{i})$の解は,左辺を因数分解して求めるか,解の公式を用いて求める. (1)2次方程式$a(x-\alpha)(x-\beta)=0$の解は,$x=\alpha, \beta$ (2)2次方程式の解の公式 2次方程式$a x^2+b x+c=0$の解は,$$x=\frac{-b \pm \sqrt{b^2-4ac}}{2 a}$$ とくに,$b=2 b^{\prime}$のとき, 2次方程式$a x^2+2 b^{\prime} x+c=0$の解は,$$x=\frac{-b^{\prime} \pm \sqrt{b^{\prime 2}-ac}}{a}$$
% 基本事項I3.3.2:2次方程式の解の個数(One More)
$b^2-4ac$を2次方程式$a x^2+b x+c=0$の判別式(discriminant)という. 2次方程式$a x^2+b x+c=0$の判別式を$D=b^2-4ac$とすると, $$\begin{aligned} &b^2-4ac>0(D>0)\Longleftrightarrow \text{異なる2つの実数解をもつ.}\\ &b^2-4 a c=0(D=0)\Longleftrightarrow \text{1つの実数解(重解)をもつ.}\\ &b^2-4ac<0(D<0)\Longleftrightarrow \text{実数解をもたない.} \end{aligned} $$ とくに,$b=2b^{\prime}$であるとき,$\frac{D}{4}=b^{\prime 2}-a c$の符号について, $$ \begin{aligned} &b^{\prime 2}-ac>0(D>0)\Longleftrightarrow \text{異なる2つの実数解をもつ.}\\ &b^{\prime 2}-ac=0(D=0)\Longleftrightarrow \text{1つの実数解(重解)をもつ.}\\ &b^{\prime 2}-ac<0(D<0)\Longleftrightarrow \text{実数解をもたない.} \end{aligned}$$
% 基本事項I3.3.3:2次関数のグラフと$x$軸の共有点(One More)
(1)2次方程式$ax^2+b x+c=0$は,2次関数$y=ax^2+b x+c$において,$y=0$とおいたものと考えることができる. 2次方程式$ax^2+bx+c=0$ の実数解は,2次関数$y=ax^2+bx+c$のグラフと$x$軸の共有点の$x$座標である. (2)(1)より,2次方程式$ax^2+bx+c=0$の実数解の個数と,$y=ax^2+bx+c$のグラフの$x$軸の共有点の個数は一致する. よって,2次方程式$ax^2+bx+c=0$の判別式を$D=b^2-4ac$とすると,$y=ax^2+bx+c$のグラフと$x$軸の位置関係は,次のようになる. $$ \begin{aligned} &D>0 \Longleftrightarrow x \text{軸と異なる2点で交わる.}\\ &D=0 \Longleftrightarrow x \text{軸に接する.}\\ &D<0 \Longleftrightarrow x \text{軸と共有点をもたない.} \end{aligned}$$
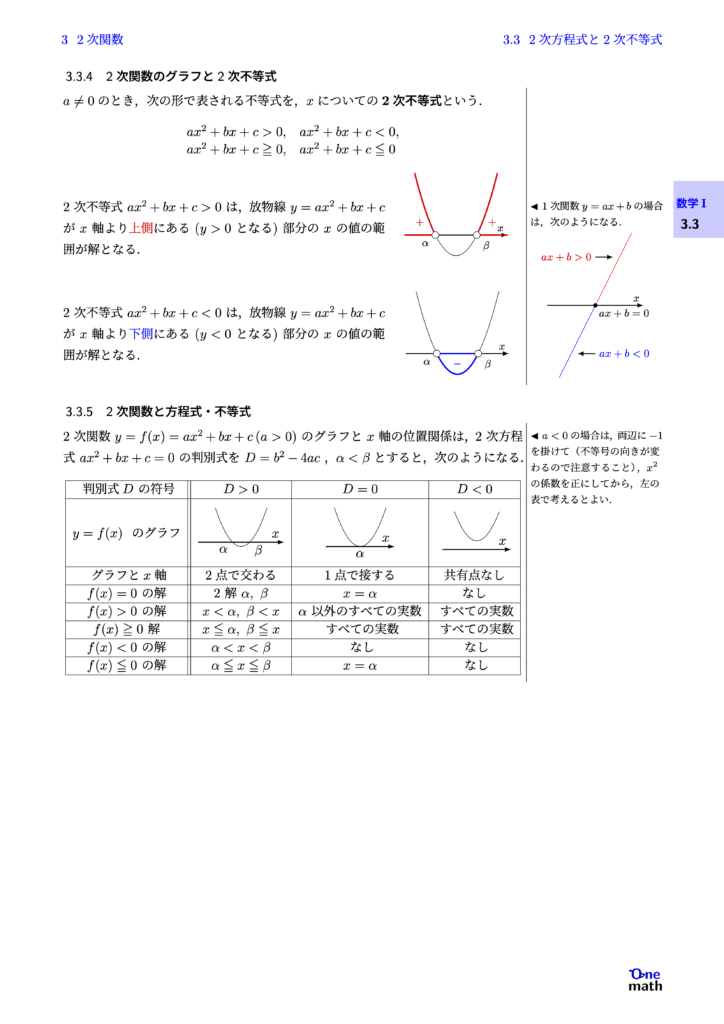
% 基本事項I3.3.4:2次関数のグラフと2次不等式(One More)
$a \neq 0$のとき,次の形で表される不等式を,$x$についての2次不等式という. $$\begin{array}{ll} ax^2+bx+c>0, & ax^2+bx+c<0, \\ ax^2+bx+c \geqq 0, & ax^2+bx+c \leqq 0 \end{array} $$ 2次不等式$ax^2+b x+c>0$は,放物線$y=ax^2+bx+c$が$x$軸より上側にある$(y>0$となる)部分の$x$の値の範囲が解となる. 2次不等式$ax^2+bx+c<0$は,放物線$y=ax^2+bx+c$が$x$軸より下側にある$(y<0$となる)部分の$x$の値の範囲が解となる.
% 基本事項I3.3.5:2次関数と方程式・不等式(One More)
2次関数$y=f(x)=ax^2+bx+c(a>0)$のグラフと$x$軸の位置関係は,2次方程式$ax^2+bx+c=0$の判別式を$D=b^2-4ac$,$\alpha<\beta$とすると,次のようになる. $$\begin{array}{|c||c|c|c|} \hline \text { 判別式 } D \text { の符号 } & D>0 & D=0 & D<0 \\ \hline y=f(x)\text { のグラフ } &&& \\ \hline \text { グラフと$x$軸 } & \text{2点で交わる} & \text{1点で接する} & \text{共有点なし} \\ \hline f(x)=0 \text { の解 } & 2 \text { 解 } \alpha, \beta & x=\alpha & \text{なし}\\ \hline f(x)>0 \text { の解 } & x<\alpha, \beta<x & \alpha \text { 以外のすべての実数}& \text { すべての実数 } \\ \hline f(x) \geqq 0 \text { 解 } & x \leqq \alpha, \beta \leqq x & \text { すべての実数 } & \text { すべての実数 } \\ \hline f(x)<0 \text { の解 } & \alpha<x<\beta & \text { なし } & \text { なし } \\ \hline f(x) \leqq 0 \text { の解 } & \alpha \leqq x \leqq \beta & x=\alpha & \text { なし } \\ \hline \end{array} $$