% 基本事項I4.1.1:三角比(One More)
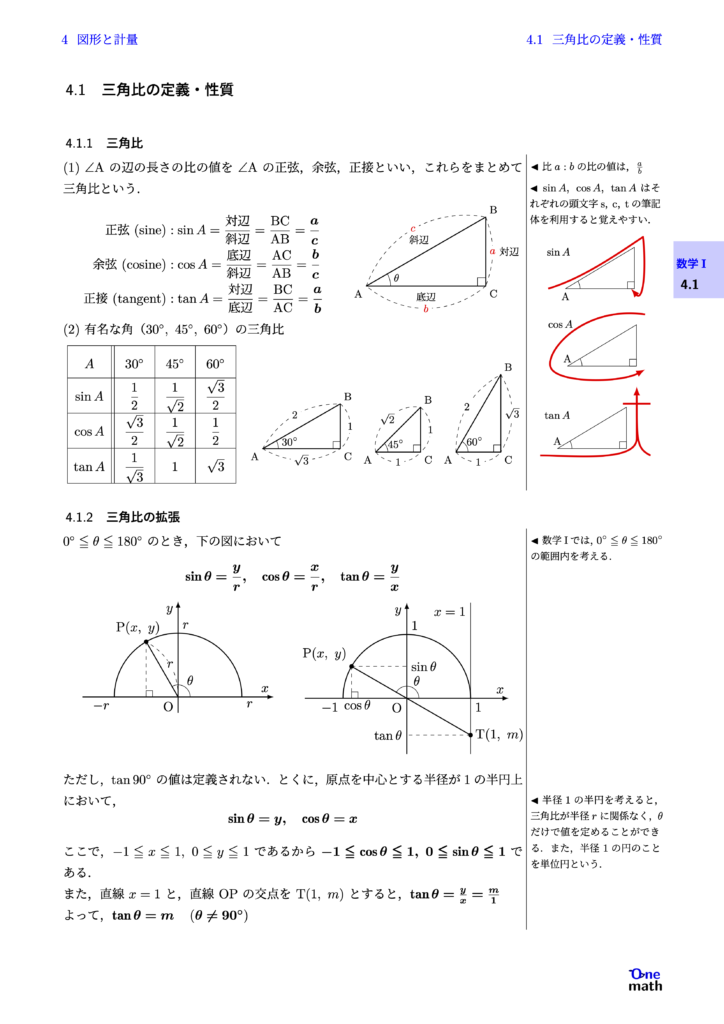
(1)$\angle \mathrm{A}$の辺の長さの比の値を$\angle \mathrm{A}$の正弦,余弦,正接といい,これらをまとめて三角比という. $$\begin{aligned} \text{正弦(sine)} &: \sin A=\frac{\text{対辺}}{\text{斜辺}}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{a}{c} \\ \text{余弦(cosine)} &: \cos A=\frac{\text{底辺}}{\text{斜辺}}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{b}{c} \\ \text{正接(tangent)} &: \tan A=\frac{\text{対辺}}{\text{底辺}}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{a}{b} \end{aligned} $$ (2)有名な角($30^{\circ}, 45^{\circ}, 60^{\circ}$)の三角比 \begin{tabular}{|c||c|c|c|}\hline $A$&$30^\circ$&$45^\circ$&$60^\circ$\\\hline $\sin{A}$&$\frac{1}{2}$&$\frac{1}{\sqrt{2}}$&$\frac{\sqrt{3}}{2}$\\\hline $\cos{A}$&$\frac{\sqrt{3}}{2}$&$\frac{1}{\sqrt{2}}$&$\frac{1}{2}$\\\hline $\tan{A}$&$\frac{1}{\sqrt{3}}$&$1$&$\sqrt{3}$\\\hline \end{tabular}\frac
% 基本事項I4.1.2:三角比の拡張(One More)
$0^{\circ} \leqq \theta \leqq 180^{\circ}$のとき,下の図において $$\sin \theta=\frac{y}{r}, \cos \theta=\frac{x}{r}, \tan \theta=\frac{y}{x}$$ ただし,$\tan 90^{\circ}$の値は定義されない.とくに,原点を中心とする半径が1の半円上において, $$ \sin \theta=y, \cos \theta=x $$ ここで,$-1 \leqq x \leqq 1, 0 \leqq y \leqq 1$であるから $-1 \leqq \cos \theta \leqq 1, 0 \leqq \sin \theta \leqq 1$である. また,直線$x=1$と,直線OPの交点を$\mathrm{T}(1, m)$とすると,$\tan \theta=\frac{y}{x}=\frac{m}{1}$ よって,$\tan \theta=m\left(\theta \neq 90^{\circ}\right)$
% 基本事項I4.1.3:三角比の値と符号(One More)
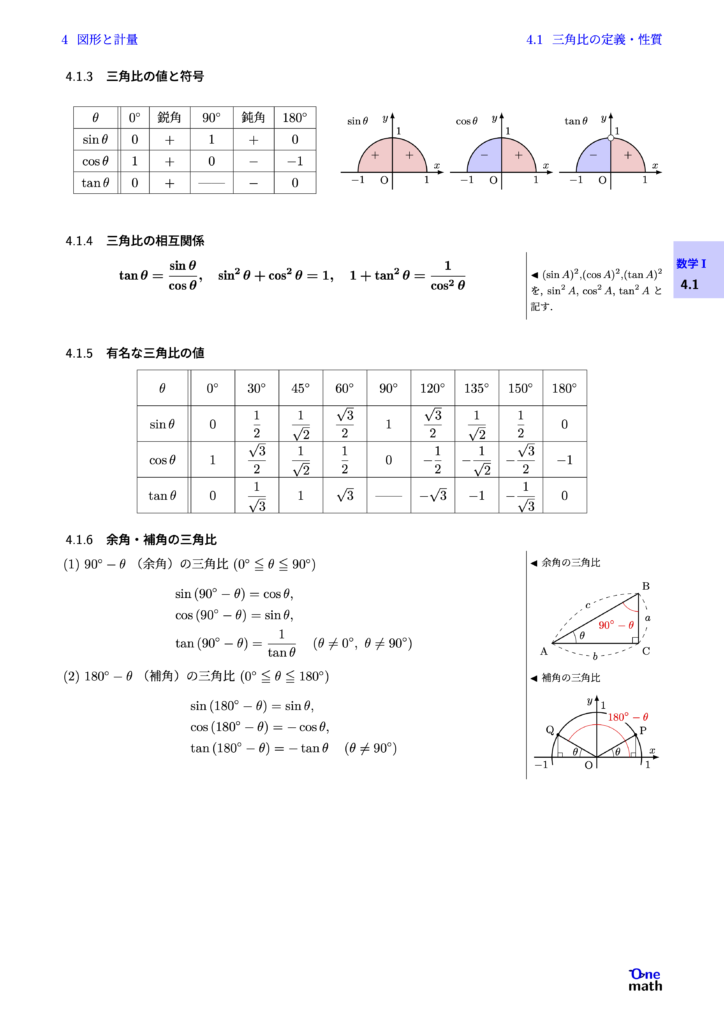
\begin{tabular}{|c||c|c|c|c|c|} \hline$\theta$ & $0^{\circ}$ & 鋭角 & $90^{\circ}$ & 鈍角 & $180^{\circ}$ \\\hline $\sin \theta$ & $0$ & $+$ & $1$ & $+$ & $0$ \\\hline $\cos \theta$ & $1$ & $+$ & $0$ & $-$ & $-1$ \\\hline $\tan \theta$ & $0$ & $+$ & ------ & $-$ & $0$ \\\hline \end{tabular}
% 基本事項I4.1.4:三角比の相互関係(One More)
$$\tan \theta=\frac{\sin \theta}{\cos \theta} , \sin ^2 \theta+\cos ^2 \theta=1, 1+\tan ^2 \theta=\frac{1}{\cos ^2 \theta}$$
% 基本事項I4.1.5:有名な三角比の値(One More)
\begin{tabular}{|c||c|c|c|c|c|c|c|c|c|} \hline $\theta$ & $0^\circ$ & $30^\circ$ & $45^\circ$ & $60^\circ$ & $90^\circ$ & $120^\circ$ & $135^\circ$ & $150^\circ$ & $180^\circ$ \\ \hline $\sin{\theta}$ & $0$ & $\frac{1}{2}$ & $\frac{1}{\sqrt{2}}$ & $\frac{\sqrt{3}}{2}$ & $1$ & $\frac{\sqrt{3}}{2}$ & $\frac{1}{\sqrt{2}}$ & $\frac{1}{2}$ & $0$ \\ \hline $\cos{\theta}$ & $1$ & $\frac{\sqrt{3}}{2}$ & $\frac{1}{\sqrt{2}}$ & $\frac{1}{2}$ & $0$ & $-\frac{1}{2}$ & $-\frac{1}{\sqrt{2}}$ & $-\frac{\sqrt{3}}{2}$ & $-1$ \\ \hline $\tan{\theta}$ & $0$ & $\frac{1}{\sqrt{3}}$ & $1$ & $\sqrt{3}$ & ------ & $-\sqrt{3}$ & $-1$ & $-\frac{1}{\sqrt{3}}$ & $0$\\ \hline \end{tabular}
% 基本事項I4.1.6:余角・補角の三角比(One More)
(1)$90^{\circ}-\theta$(余角)の三角比$\left(0^{\circ} \leqq \theta \leqq 90^{\circ}\right)$ $$\begin{aligned} & \sin \left(90^{\circ}-\theta\right)=\cos \theta, \\ & \cos \left(90^{\circ}-\theta\right)=\sin \theta, \\ & \tan \left(90^{\circ}-\theta\right)=\frac{1}{\tan \theta} \left(\theta \neq 0^{\circ}, \theta \neq 90^{\circ}\right)\end{aligned}$$ (2)$180^{\circ}-\theta$(補角)の三角比$\left(0^{\circ} \leqq \theta \leqq 180^{\circ}\right)$ $$\begin{aligned} & \sin \left(180^{\circ}-\theta\right)=\sin \theta, \\ & \cos \left(180^{\circ}-\theta\right)=-\cos \theta, \\ & \tan \left(180^{\circ}-\theta\right)=-\tan \theta \left(\theta \neq 90^{\circ}\right)\end{aligned}$$
% 基本事項I4.2.1:正弦定理(One More)
三角形の外接円の半径を$R$とすると, $$ \frac{a}{\sin{A}}=\frac{b}{\sin {B}}=\frac{c}{\sin{C}}=2 R $$
% 基本事項I4.2.2:余弦定理(One More)
$$ \begin{aligned} & a^2=b^2+c^2-2 bc \cos {A}, \\ & b^2=c^2+a^2-2 ca \cos {B}, \\ & c^2=a^2+b^2-2 ab \cos {C} \end{aligned} $$ 式を整理すると,次の等式が得られる. $$ \begin{aligned} &\cos{A}=\frac{b^2+c^2-a^2}{2bc},\\ &\cos{B}=\frac{c^2+a^2-b^2}{2ca},\\ &\cos{C}=\frac{a^2+b^2-c^2}{2ab} \end{aligned} $$
% 基本事項I4.2.3:角と辺の大小関係(One More)
$\triangle \mathrm{ABC}$において,$\mathrm{AB}=c, \mathrm{BC}=a, \mathrm{CA}=b$とする.ここで,$\angle \mathrm{A}$が鋭角,直角,鈍角であるとき,それぞれ,$\cos A>0$,$\cos A=0$,$\cos A<0$であることから,次の関係がいえる. $$A \text{ が鋭角 } \Longleftrightarrow b^2+c^2>a^2,$$ $$A \text{ が直角 } \Longleftrightarrow b^2+c^2=a^2,$$ $$A \text{ が鈍角 }\Longleftrightarrow b^2+c^2<a^2$$ また,角の大小と辺の大小は一致する.すなわち, $$ A>B \Longleftrightarrow a>b $$
% 基本事項I4.3.1:三角形の面積(One More)
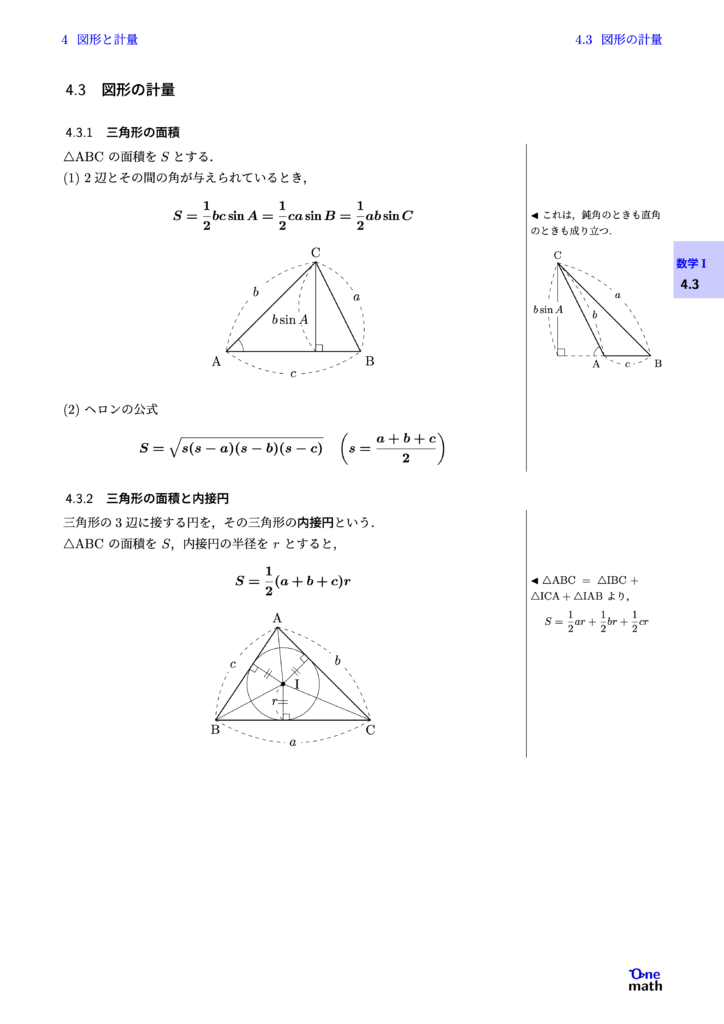
$\triangle \mathrm{ABC}$の面積を$S$とする. (1)2辺とその間の角が与えられているとき,$$S=\frac{1}{2} b c \sin A=\frac{1}{2} c a \sin B=\frac{1}{2} ab \sin C$$ (2)ヘロンの公式$$S=\sqrt{s(s-a)(s-b)(s-c)} \left(s=\frac{a+b+c}{2}\right)$$
% 基本事項I4.3.2:三角形の面積と内接円(One More)
三角形の3辺に接する円を,その三角形の内接円という. $\triangle \mathrm{ABC}$の面積を$S$,内接円の半径を$r$とすると, $$ S=\frac{1}{2}(a+b+c)r $$