% 節末I3.1.1★
関数$f(x)=3x^2-2x+2$について,$f(f(a))$の値を求めよ.
% 節末I3.1.2★★
2つの放物線$y=3x^2-18x+25$と$y=ax^2+8x+b$の頂点が一致するように定数$a, b$の値を定めよ.
% 節末I3.1.3★★
$y=ax^2+bx+c$で表される放物線が点$(1,-2)$に関して放物線$y=-3x^2$と点対称であるとき,定数$a, b, c$の値を求めよ.
% 節末I3.1.4★★
放物線$y=x^2-4x+1$を$x$軸方向に3だけ平行移動し,さらに直線$y=2$に関して折り返してできる放物線の方程式を求めよ.
% 節末I3.1.5★★★
次の関数$f(x)$の最小値とそのときの$x$の値を求めよ. (1)$f(x)=|x-2|+|x-4|+|x-6|$ (2)$f(x)=|x+|2x-10||$
% 節末I3.2.1★★
関数$y=x^2-6x+k+3(-1 \leqq x \leqq 3)$の最大値と最小値の和が$0$であるとき,定数$k$の値とそのときの最大値,最小値を求めよ.
% 節末I3.2.2★★★★
2次関数$y=-2x^2+8x$について,次の問いに答えよ. (1)この関数のグラフの頂点,$x$軸の共有点,$y$軸の共有点の座標を求め,グラフをかけ. (2)$a \leqq x \leqq a+1$における関数の最大値が6であるような定数$a$の値を求めよ.
% 節末I3.2.3★★
$a$を定数として,関数$y=\left(x^2-4x\right)^2+2a\left(x^2-4x\right)+a+2$の最小値を$m$とする.このとき,次の問いに答えよ.
% 節末I3.2.4★★★
放物線$y=ax^2+bx+c$は,頂点の座標が$(3, 7)$で,点$(6,-5)$を通る.このとき,定数$a, b, c$の値を求めよ.
% 節末I3.2.5★★★
$a>0, b>0, a+b=1$のとき,$a^3+b^3$の最小値を求めよ.
% 節末I3.2.6★★★
2次関数$f(x)=ax^2+bx+c$が,$f(-2)=f(4)=0$を満たし,その最大値が9であるとき,定数$a, b, c$の値を求めよ.
% 節末I3.3.1★★
2次方程式$x^2+4x+7a=0$,$2x^2-6x-a=0$がともに実数解をもつ整数$a$の個数を求めよ.
% 節末I3.3.2★★★
実数$x, y$が$x^2+y^2=13$のもとで,$x-ay$の最大値が7となるとき,定数$a$の値を求めよ.
% 節末I3.3.3★★★
(1)不等式$3x^4-7x^2+2>0$を解け. (2)不等式$\left(x^2-3x+2\right)^2-4\left(x^2-3x+2\right)+3 \leqq 0$を解け.
% 節末I3.3.4★★★★
$a$を定数とする.$x$についての方程式$|(x-3)(x-5)|=ax-2a+\frac{1}{2}$が異なる4つの実数解をもつとき,$a$の値の範囲を求めよ.
% 節末I3.3.5★★★
2次不等式$x^2-3x-4<|x-2|$を満たす$x$の値の範囲を求めよ.
% 章末I3.1★★★
実数$x, y$が$x^2-xy+y^2+y-5=0$を満たすとき,$y$の最大値は$\fbox{ }$であり,最小値は$\fbox{ }$である.
% 章末I3.2★★
2つの放物線$y=x^2+4$,$y=-x^2+4x$の両方に接する直線の方程式を求めよ.
% 章末I3.3★★★
$a, b$は自然数で,2次方程式$x^2+2ax+4a-4b=0$が重解$\alpha$をもつとき,$a, b, \alpha$の値を求めよ.
% 章末I3.4★★★
$a, b$を異なる実数とするとき,$x$に関する方程式$(x-3a)(x-3b)-(3x-4a-5b)=0$は異なる2つの実数解をもつことを証明せよ.
% 章末I3.5★★★
方程式$4x^2+3xy+4y^2=9$を満たす$x, y$に対して,$u=x+y, v=xy$とおく. (1)$u^2-4v \geqq 0$を示せ. (2)$u, v$の間に成り立つ等式を求めよ. (3)$k=u+v$がとる値の範囲を求めよ.
% 解答（節末）I3.1.1
$f(x)$の式に,$x=f(a)=3a^2-2a+2$を代入して, $$\begin{aligned} f(f(a))&=3\left(3a^2-2a+2\right)^2-2\left(3a^2-2a+2\right)+2 \\ &=27a^4-36a^3+42a^2-20a+10 \end{aligned}$$
% 解答（節末）I3.1.2
$$y=3x^2-18x+25=3\left(x^2-6x\right)+25 =3(x-3)^2-2, $$ $$ \begin{aligned} y &=ax^2+8x+b \\ &=a\left(x^2+\frac{8}{a}x\right)+b \\ &=a\left(x+\frac{4}{a}\right)^2-a\left(\frac{4}{a}\right)^2+b \\ &=a\left(x+\frac{4}{a}\right)^2-\frac{16}{a}+b \end{aligned} $$ よって,2つの放物線の頂点の座標は,それぞれ, $$ (3,-2), \left(-\frac{4}{a},-\frac{16}{a}+b\right) $$ 与えられた条件より, $$ 3=-\frac{4}{a},-2=-\frac{16}{a}+b $$ これを解くと,$a=-\frac{4}{3}, b=-14$ 別解：放物線$y=3x^2-18x+25$の頂点は,点$(3,-2)$ したがって,2つの放物線の頂点が一致するための条件は,$y=ax^2+8x+b$が$y=a(x-3)^2-2\cdots(\mathrm{i})$と表されることであるから,(i)を展開すると, $$ y=ax^2-6ax+9a-2 $$ これと$y=ax^2+8x+b$の係数を比較すると, $ 8=-6a, b=9a-2$ これを解くと,$a=-\frac{4}{3}, b=-14$
% 解答（節末）I3.1.3
放物線$y=-3x^2$の頂点は点$(0, 0)$ この点を点$(1,-2)$に関して対称に移動すると,点$(2,-4)$となる. もとのグラフの$x^2$の係数が$-3$であるから,移動したグラフは下に凸の放物線であり,$x^2$の係数は$3$である. したがって,点$(1,-2)$に関して放物線$y=-3x^2$と点対称である放物線の方程式は $$ y=3(x-2)^2-4=3x^2-12x+8 $$ よって,$a=3, b=-12, c=8$
% 解答（節末）I3.1.4
$$ y=x^2-4x+1=(x-2)^2-3 $$ したがって,もとの放物線$y=x^2-4x+1$の頂点は点$(2,-3)$である. この頂点を$x$軸方向に3だけ平行移動すると,点$(5,-3)$となる. さらに,直線$y=2$に関して折り返すと,頂点は点$(5, 7)$となる. もとのグラフの$x^2$の係数が$1$であるから,移動したグラフは上に凸の放物線であり,$x^2$の係数は$-1$である. よって,$y=-(x-5)^2+7$
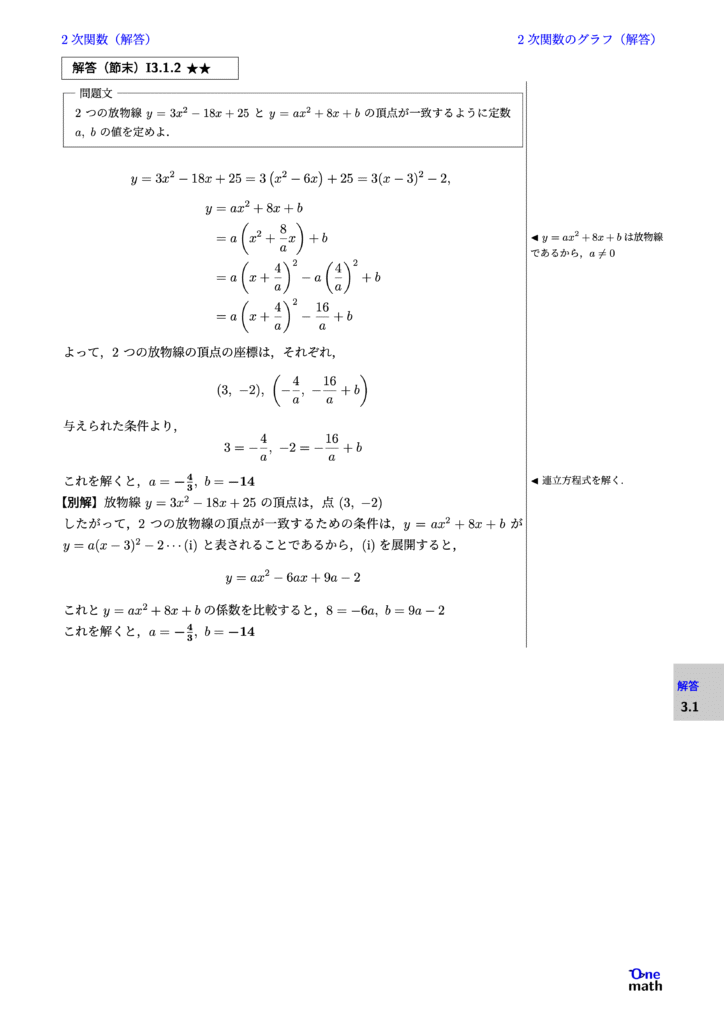
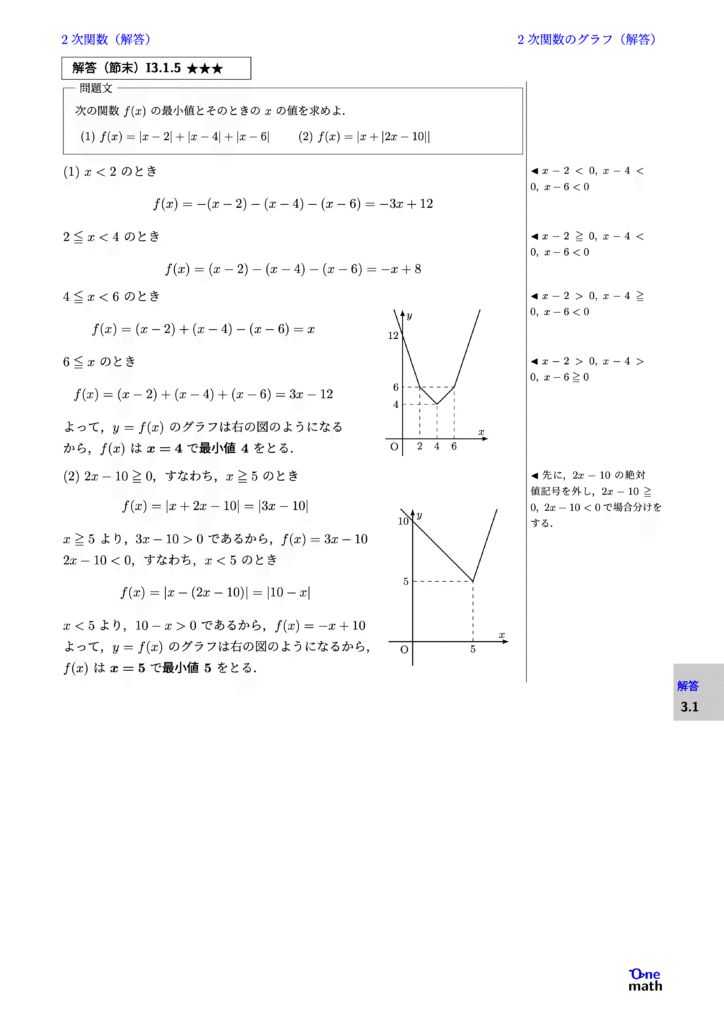
% 解答（節末）I3.1.5
(1)$x<2$のとき $$ f(x)=-(x-2)-(x-4)-(x-6)=-3x+12 $$ $2 \leqq x<4$のとき $$ f(x)=(x-2)-(x-4)-(x-6)=-x+8 $$ $4 \leqq x<6$のとき $$ f(x)=(x-2)+(x-4)-(x-6)=x $$ $6 \leqq x$のとき $$ f(x)=(x-2)+(x-4)+(x-6)=3x-12 $$ よって,$y=f(x)$のグラフは右の図の ようになるから,$f(x)$は $x=4$で最小値4をとる. (2)$2x-10 \geqq 0$,すなわち,$x \geqq 5$のとき $$ f(x)=|x+2x-10|=|3x-10| $$ $x \geqq 5$より,$3x-10>0$であるから,$f(x)=3x-10$ $2x-10<0$,すなわち,$x<5$のとき $$ f(x)=|x-(2x-10)| =|10-x| $$ $x<5$より,$10-x>0$であるから, $ f(x)=-x+10 $ よって,$y=f(x)$のグラフは右の図のようになるから,$f(x)$は $x=5$で最小値5をとる.
% 解答（節末）I3.2.1
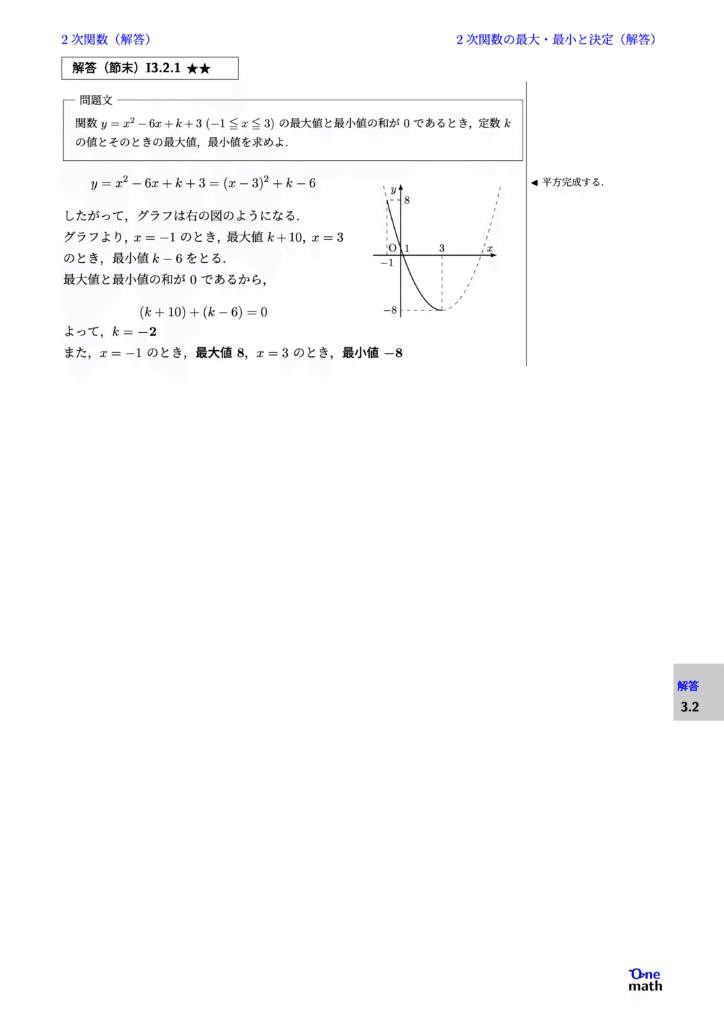
$$ y=x^2-6x+k+3 =(x-3)^2+k-6 $$ したがって,グラフは右の図のようになる. グラフより,$x=-1$のとき,最大値$k+10$,$x=3$のとき,最小値$k-6$をとる. 最大値と最小値の和が$0$であるから, $$ (k+10)+(k-6)=0 $$ よって,$k=-2$ また,$x=-1$のとき,最大値$8$,$x=3$のとき,最小値$-8$
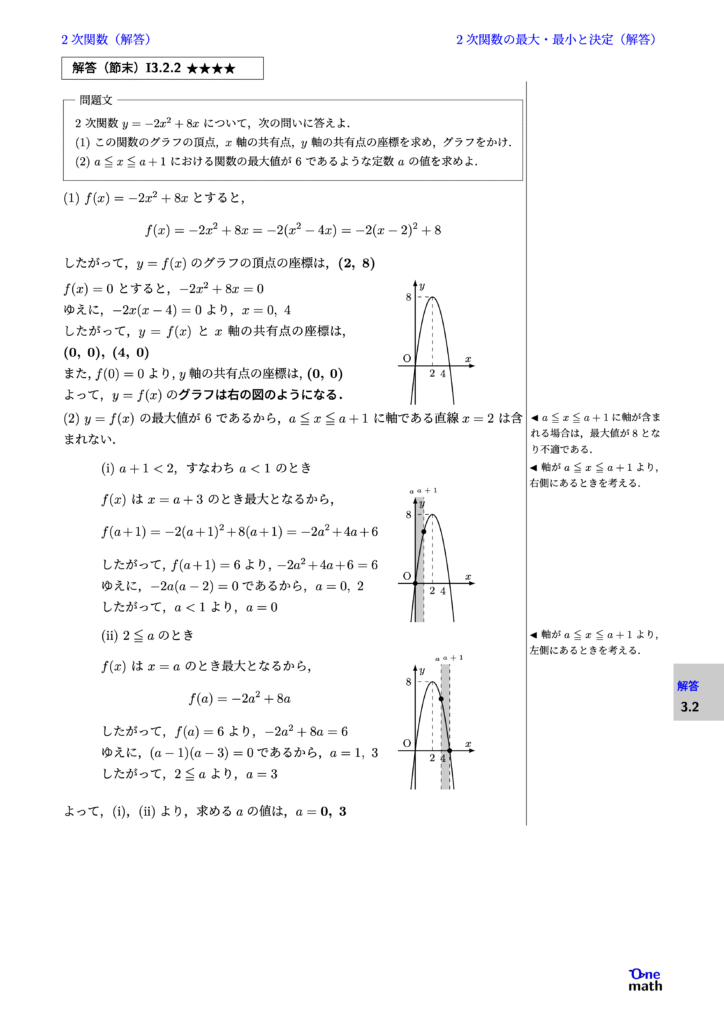
% 解答（節末）I3.2.2
(1) $f(x)=-2x^2+8x$とすると, $$ f(x)=-2x^2+8x=-2(x^2-4x)=-2(x-2)^2+8 $$ したがって,$y=f(x)$のグラフの頂点の座標は,$(2, 8)$ $f(x)=0$とすると,$ -2x^2+8x=0 $ ゆえに,$-2x(x-4)=0$より,$x=0, 4$ したがって,$y=f(x)$と$x$軸の共有点の座標は,$(0, 0),(4, 0)$ また,$f(0)=0$より,$y$軸の共有点の座標は,$(0, 0)$ よって,$y=f(x)$のグラフは右の図のようになる. (2)$y=f(x)$の最大値が6であるから,$a \leqq x \leqq a+1$に軸である直線$x=2$は含まれない. (i)$a+1<2$,すなわち$a<1$のとき $f(x)$は$x=a+3$のとき最大となるから, $$ f(a+1)=-2(a+1)^2+8(a+1)=-2a^2+4a+6 $$ したがって,$f(a+1)=6$より,$-2a^2+4a+6=6$ ゆえに,$-2a(a-2)=0$であるから,$a=0, 2$ したがって,$a<1$より,$a=0$ (ii)$2 \leqq a$のとき $f(x)$は$x=a$のとき最大となるから, $$ f(a)=-2a^2+8a $$ したがって,$f(a)=6$より,$-2a^2+8a=6$ ゆえに,$(a-1)(a-3)=0$であるから,$a=1, 3$ したがって,$2 \leqq a$より,$a=3$ よって,(i),(ii)より,求める$a$の値は,$a=0, 3$
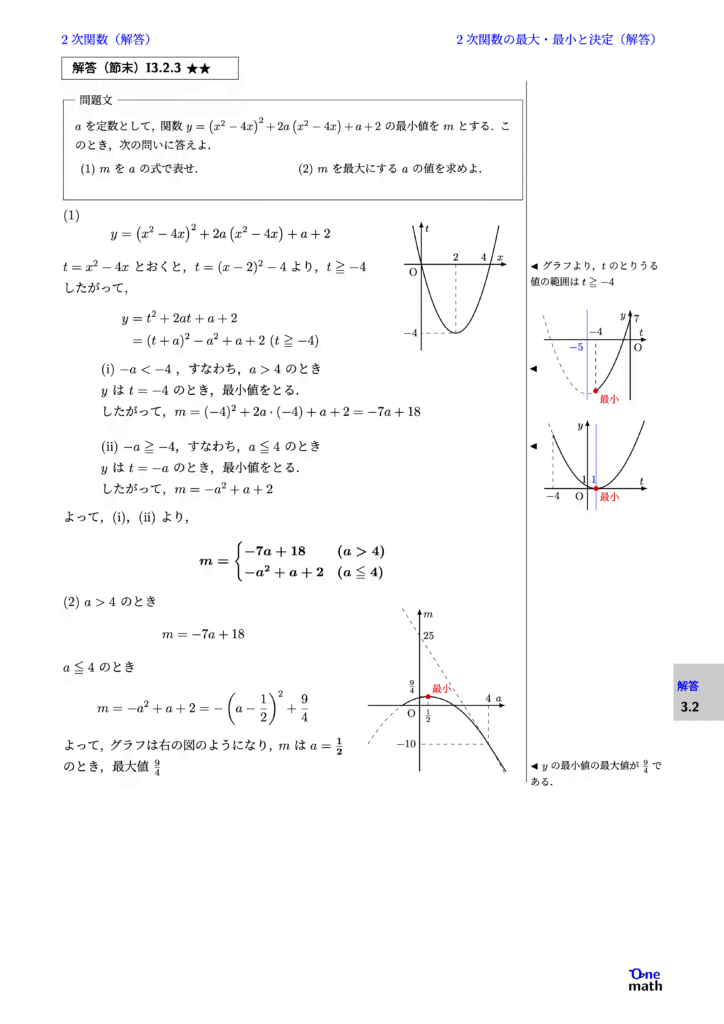
% 解答（節末）I3.2.3
(1) $$ y=\left(x^2-4x\right)^2+2a\left(x^2-4x\right)+a+2$$ $t=x^2-4x$とおくと, $t=(x-2)^2-4$より,$t \geqq -4$ したがって, $$ \begin{aligned} y &=t^2+2at+a+2 \\ &=(t+a)^2-a^2+a+2(t \geqq -4) \end{aligned} $$ (i)$-a<-4$,すなわち,$a>4$のとき $y$は$t=-4$のとき,最小値をとる. したがって,$m=(-4)^2+2a\cdot(-4)+a+2=-7a+18$ (ii)$-a \geqq -4$,すなわち,$a \leqq 4$のとき $y$は$t=-a$のとき,最小値をとる. したがって,$m=-a^2+a+2$ よって,(i),(ii)より, $$ m=\begin{cases}-7a+18 &(a>4)\\-a^2+a+2 &(a \leqq 4)\end{cases} $$ (2)$a>4$のとき $$ m=-7a+18 $$ $a \leqq 4$のとき $$ m=-a^2+a+2=-\left(a-\frac{1}{2}\right)^2+\frac{9}{4} $$ よって,グラフは右の図のようになり,$m$は$a=\frac{1}{2}$のとき,最大値$\frac{9}{4}$
% 解答（節末）I3.2.4
頂点が点$(3, 7)$であるから,求める放物線は, $$ y=a(x-3)^2+7 $$ と表される. この放物線が,点$(6,-5)$を通るから, $$ -5=a(6-3)^2+7 $$ したがって$a=-\frac{4}{3}$ このとき, $ y=-\frac{4}{3}(x-3)^2+7=-\frac{4}{3}x^2+8x-5 $ これが,$y=ax^2+bx+c$と一致するので,$b=8, c=-5$ よって,$a=-\frac{4}{3}, b=8, c=-5$
% 解答（節末）I3.2.5
$a+b=1$から,$b=1-a\cdots(\mathrm{i})$ $b>0$であるから,$1-a>0$ したがって,$a<1$ $a>0$との共通範囲は,$0<a<1\cdots(\mathrm{ii})$ $a^3+b^3=t$とすると, $$t=a^3+(1-a)^3=3 a^2-3 a+1 =3\left(a-\frac{1}{2}\right)^2+\frac{1}{4}$$ (ii)において,$t$は$a=\frac{1}{2}$のとき,最小値$\frac{1}{4}$ $a=\frac{1}{2}$のとき,(i)から$b=\frac{1}{2}$ よって,$a=\frac{1}{2}, b=\frac{1}{2}$のとき,最小値$\frac{1}{4}$
% 解答（節末）I3.2.6
$f(-2)=f(4)=0$であるから,放物線$y=f(x)$の軸は,2点$(-2, 0),(4, 0)$を結ぶ線分の中点$(1, 0)$を通る. したがって,$f(x)$は$x=1$で最大値9をとり,$f(x)$は$f(x)=a(x-1)^2+9(a<0)$と表される. $f(-2)=0$から,$9a+9=0$ ゆえに,$a=-1$ これは,$a<0$を満たす. したがって,$f(x)=-(x-1)^2+9$ 展開すると,$f(x)=-x^2+2x+8$である. よって,$a=-1, b=2, c=8$となる. 別解：$f(-2)=f(4)=0$であるから,$f(x)=a(x+2)(x-4)$と表される. 展開すると,$a(x+2)(x-4)=a(x^2-2x-8)=a(x-1)^2-9a$であるから,$f(x)=a(x-1)^2-9a$ 最大値が9であるから,$ a<0$かつ$-9a=9$ したがって,$a=-1$ これは$a<0$を満たす. ゆえに,$f(x)=-(x+2)(x-4)=-x^2+2x+8$ よって,$a=-1, b=2, c=8$
% 解答（節末）I3.3.1
2次方程式$x^2+4x+7a=0$の判別式を$D_1$とすると, $\frac{D_1}{4}=2^2-1\cdot 7a=4-7a$ 2次方程式が実数解をもつから,$D_1 \geqq 0$ したがって,$4-7a \geqq 0$ ゆえに,$a \leqq \frac{4}{7}\cdots(\mathrm{i})$ 2次方程式$2x^2-6x-a=0$の判別式を$D_2$とすると, $\frac{D_2}{4}=(-3)^2-2\cdot(-a)=9+2a$ 2次方程式が実数解をもつから,$D_2 \geqq 0$ したがって,$9+2a \geqq 0$ ゆえに,$a \geqq -\frac{9}{2}\cdots(\mathrm{ii})$ したがって,(i)と(ii)の共通範囲を求めると,$$-\frac{9}{2} \leqq a \leqq \frac{4}{7}$$ この不等式を満たす整数$a$は,$a=-4,-3,-2,-1, 0$ よって,求める整数$a$の個数は,5個
% 解答（節末）I3.3.2
$ x-ay=k$とおくと,$x=k+ay $ これを$x^2+y^2=13$に代入すると,$(k+ay)^2+y^2=13$ したがって,$(a^2+1)y^2+2ak y+k^2-13=0$ $y$は実数であるから,この2次方程式の判別式を$D$とすると,$D \geqq 0$ $$ \frac{D}{4}=(ak)^2-(a^2+1)(k^2-13) =-k^2+13(a^2+1) $$ これより,$-k^2+13(a^2+1) \geqq 0$ ゆえに,$ k^2 \leqq 13(a^2+1)$ したがって,$-\sqrt{13(a^2+1)} \leqq k \leqq \sqrt{13(a^2+1)}$ $k$の最大値が7であるから, $\sqrt{13(a^2+1)}=7 $ よって,$a^2=\frac{36}{13}$ これを解いて,$a=\pm \frac{6}{\sqrt{13}}$
% 解答（節末）I3.3.3
(1)$x^2=t$とおくと,$t \geqq 0$ 与えられた不等式は,$3t^2-7t+2>0$ したがって,$(3t-1)(t-2)>0$ これを解くと,$0 \leqq t<\frac{1}{3}, 2<t$ ゆえに,$0 \leqq x^2<\frac{1}{3}, 2<x^2$ ここで,$x^2 \geqq 0$は常に成り立つので, $x^2<\frac{1}{3}$より,$-\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}}$ $2<x^2$より,$x<-\sqrt{2}, \sqrt{2}<x$ よって,$x<-\sqrt{2},-\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}}, \sqrt{2}<x$ (2)$x^2-3x+2=t$とおくと,$t=\left(x-\frac{3}{2}\right)^2-\frac{1}{4}$である. $t$のとりうる値の範囲は,$t \geqq -\frac{1}{4}$ 不等式を$t$で表すと,$t^2-4t+3 \leqq 0$ したがって,$(t-1)(t-3) \leqq 0$より,$1 \leqq t \leqq 3$ これは$t \geqq -\frac{1}{4}$を満たす. ゆえに,$1 \leqq x^2-3x+2 \leqq 3$ $1 \leqq x^2-3x+2$より,$x^2-3x+1 \geqq 0$ $x^2-3x+1=0$を解くと,$x=\frac{3\pm \sqrt{5}}{2}$ このとき,$x^2-3x+1 \geqq 0$の解は, $$x \leqq \frac{3-\sqrt{5}}{2}, \frac{3+\sqrt{5}}{2} \leqq x\cdots(\mathrm{i})$$ $x^2-3x+2 \leqq 3$より,$x^2-3x-1 \leqq 0$ $x^2-3x-1=0$を解くと,$x=\frac{3 \pm \sqrt{13}}{2}$ このとき,$x^2-3x-1 \leqq 0$の解は, $$ \frac{3-\sqrt{13}}{2} \leqq x \leqq \frac{3+\sqrt{13}}{2}\cdots(\mathrm{ii}) $$ よって,(i),(ii)の共通範囲を求めると, $$ \frac{3-\sqrt{13}}{2} \leqq x \leqq \frac{3-\sqrt{5}}{2}, \frac{3+\sqrt{5}}{2} \leqq x \leqq \frac{3+\sqrt{13}}{2} $$
% 解答（節末）I3.3.4
$$ y=|(x-3)(x-5)| \cdots(\mathrm{i}) , y=ax-2a+\frac{1}{2} \cdots(\mathrm{ii}) $$ とする. $(x-3)(x-5) \geqq 0$の解は,$x \leqq 3, 5 \leqq x$ $(x-3)(x-5)<0$の解は,$3<x<5$ したがって,(i)は, $x \leqq 3, 5 \leqq x$のとき,$y=(x-3)(x-5)=(x-4)^2-1$ $3<x<5$のとき,$y=-(x-3)(x-5)=-(x-4)^2+1$ よって,(i)のグラフは右の図のようになる. (ii)は,$y=a(x-2)+\frac{1}{2}$と変形できるから,(ii)のグラフは定点$\left(2, \frac{1}{2}\right)$を通る傾き$a$の直線である. （ア）(ii)のグラフが(i)のグラフの$3 \leqq x \leqq 5$の部分と接するとき このとき,2次方程式$-(x-3)(x-5)=ax-2a+\frac{1}{2}$,すなわち,$x^2+(a-8)x-2a+\frac{31}{2}=0$の判別式を$D$とすると, $$ D=(a-8)^2-4\cdot 1\cdot \left(-2a+\frac{31}{2}\right)=a^2-8a+2 $$ $D=0$より,$a^2-8a+2=0$ これを解いて,$a=4\pm \sqrt{14}$ このとき,$3 \leqq x \leqq 5$の部分と接するのは,$a=4-\sqrt{14}$のときである. （イ）(ii)のグラフが点$(5, 0)$を通るとき $0=5a-2a+\frac{1}{2}$より,$a=-\frac{1}{6}$ よって,（ア）,（イ）より,方程式$|(x-3)(x-5)|=ax-2a+\frac{1}{2}$が相異なる4つの実数解をもつとき,$a$の値の範囲は, $$ -\frac{1}{6}<a<4-\sqrt{14} $$
% 解答（節末）I3.3.5
$$ \begin{aligned} |x-2| &=\begin{cases} x-2 &(x \geqq 2)\\ -x+2 &(x<2) \end{cases} \end{aligned} $$ $x^2-3x-4=(x-\frac{3}{2})^2-\frac{25}{4}$であるから,$y=x^2-3x-4$のグラフと$y=|x-2|$のグラフは,右の図のようになる. 2つのグラフの交点の$x$座標は, (i)$x \geqq 2$のとき $x^2-3x-4=x-2$より,$x^2-4x-2=0$ したがって,$x=2 \pm \sqrt{6}$ ゆえに,$x \geqq 2$より,$x=2+\sqrt{6}$ (ii)$x<2$のとき $x^2-3x-4=-(x-2)$より,$x^2-2x-6=0 $ したがって,$x=1 \pm \sqrt{7}$ ゆえに,$x<2$より,$x=1-\sqrt{7}$ よって,(i),(ii)とグラフより,求める$x$の値の範囲は,$1-\sqrt{7}<x<2+\sqrt{6}$ 別解： (i)$x \geqq 2$のとき $x^2-3x-4<x-2 $より,$x^2-4x-2<0 $ ゆえに,$2-\sqrt{6}<x<2+\sqrt{6}$ これと$x \geqq 2$より,$2 \leqq x<2+\sqrt{6}$ (ii)$x<2$のとき $x^2-3x-4<-(x-2)$より,$x^2-2x-6<0 $ ゆえに,$1-\sqrt{7}<x<1+\sqrt{7}$ これと$x<2$より,$ 1-\sqrt{7}<x<2 $ よって,(i),(ii)より,求める$x$の値の範囲は,$1-\sqrt{7}<x<2+\sqrt{6}$
% 解答（章末）I3.1
$y$が$k$という値をとるとすると,$x^2-kx+k^2+k-5=0 \cdots(\mathrm{i})$ を満たす実数$x$が存在する. したがって,この条件は,(i)の判別式を$D$とすると, $$D=(-k)^2-4\left(k^2+k-5\right)$$ $D \geqq 0$であるから,$ k^2-4k^2-4k+20 \geqq 0$ ゆえに,$-3k^2-4k+20 \geqq 0$より,$(3k+10)(k-2) \leqq 0$ したがって,$-\frac{10}{3} \leqq k \leqq 2$ よって,$y$の最大値は$2$,最小値は$-\frac{10}{3}$
% 解答（章末）I3.2
求める直線の方程式を$y=ax+b \cdots(\mathrm{i})$とおく. 直線(i)と放物線$y=x^2+4$が接するから, $ x^2+4=ax+b $ すなわち,$x^2-ax+(4-b)=0$ この2次方程式の判別式を$D_1$とすると, $ D_1=(-a)^2-4 \cdot 1 \cdot(4-b) $ したがって,$D_1=0$より,$a^2+4b-16=0 \cdots(\mathrm{ii})$ 直線(i)と放物線$y=-x^2+4x$が接するから, $ -x^2+4x=ax+b$ すなわち,$x^2+(a-4)x+b=0$ この2次方程式の判別式を$D_2$とすると, $ D_2=(a-4)^2-4 \cdot 1 \cdot b $ したがって,$D_2=0$より,$a^2-8a+16-4b=0$ ゆえに,$4b=a^2-8a+16 \cdots(\mathrm{iii})$ (iii)を(ii)に代入して整理すると, $$ 2a^2-8a=0 $$ したがって,$2a(a-4)=0$より,$a=0, 4$ $a=0$のとき,(ii)より,$b=4$ $a=4$のとき,(ii)より,$b=0$ よって,求める直線の方程式は,$y=4, y=4x$
% 解答（章末）I3.3
2次方程式$x^2+2ax+4a-4b=0$の判別式を$D$とすると, $$ \frac{D}{4}=a^2-1\cdot(4a-4b) =a^2-4a+4b $$ 2次方程式が重解をもつから,$D=0$ 整理すると,$4b=a(4-a)\cdots(\mathrm{i})$ ここで,$a, b$は自然数より,$4b>0$かつ$a>0$ したがって,$4-a>0$より, $ 0<a<4 $ $a$は自然数であるから,$a=1, 2, 3$ これらのうち,(i)より,$b$が自然数となるのは,$a=2$のときである. ゆえに,$b=1$ このとき,$x^2+2ax+4a-4b=0$の重解は,$x=-\frac{2a}{2}=-a$ したがって,$a=2$より,重解は$-2$となる. よって,$a=2, b=1, \alpha=-2$
% 解答（章末）I3.4
与えられた方程式を整理すると, $$ x^2-3(a+b+1)x+9ab+4a+5b=0 $$ この2次方程式の判別式を$D$とすると, $$ D=\{3(a+b+1)\}^2-4\cdot 1\cdot \{9ab+4a+5b\} =9(a-b)^2+2(a-b)+9 $$ ここで,$a-b=c$とおくと, $$ D=9c^2+2c+9=\left(3c+\frac{1}{3}\right)^2+\frac{80}{9} $$ よって,この方程式は$D>0$であるから,相異なる2つの実数解をもつ.$\blacksquare$ 別解： $f(x)=(x-3a)(x-3b)-(3x-4a-5b)$とする.方程式が異なる2つの実数解をもつことを示すには,$y=f(x)$が$x$軸と異なる2点で交わることを示せばよい. $$ f(3a)=-5(a-b), f(3b)=4(a-b) $$ より,$a \neq b$であるから,$f(3a)$と$f(3b)$は異符号であり,一方は負である. よって,$y=f(x)$は$x$軸と異なる2点で交わる.$\blacksquare$
% 解答（章末）I3.5
(1)$$u^2-4v=(x+y)^2-4xy=x^2-2xy+y^2=(x-y)^2 \geqq 0$$ よって,$u^2-4v \geqq 0$が成り立つ. (2)$x^2+y^2=(x+y)^2-2xy$であるから,与えられた方程式は, $$ 4\left\{(x+y)^2-2xy\right\}+7xy=15 $$ したがって,$4(x+y)^2-xy=15$ よって,$4u^2-v=15$ (3)$u^2-4v \geqq 0\cdots(\mathrm{i}), 4u^2-v=15\cdots(\mathrm{ii})$とする. (ii)より,$v=4u^2-15$ これを(i)に代入すると, $ u^2-4(4u^2-15) \geqq 0 $ したがって, $ u^2-4 \leqq 0 $ ゆえに,$-2 \leqq u \leqq 2\cdots(\mathrm{iii})$ $k$を$u$の式で表すと,(ii)より, $$ k=u+v=u+4u^2-15=4\left(u+\frac{1}{8}\right)^2-\frac{241}{16} $$ (iii)より,$k$は$u=2$で最大値$3$,$u=-\frac{1}{8}$で最小値$-\frac{241}{16}$ よって,$$-\frac{241}{16} \leqq k \leqq 3$$
