% 基本事項A1.1.1:集合(One More)
(1) 明確な範囲をもつ事物の集まりを集合という .また,集合に属する1つ1つのものを,その集合の要素という . ある要素$a$が集合$A$に含まれる場合,$a$は集合$A$に属するといい,$a \in A$と表す.逆に,要素$b$が集合$A$に含まれない場合には,$b \notin A$と表す.このとき,任意の要素$a$と集合$A$の関係において,$a \in A$または$a \notin A$のいずれかが成り立つ.要素が有限個である集合を有限集合,要素の数が無限に存在する集合を無限集合という. (2)集合を表すには,次の2つの方法がある. (i)要素を列記する方法 (ii)要素の満たす条件を述べて表す方法 例えば,1桁の正の奇数の集合を$A$とすると,$A$には次のような表し方がある. (i)$A=\{1,3,5,7,9\}$ (ii)$A=\{x \mid 1 \leqq x \leqq 9,x \text{は奇数} \},A=\{2 n-1 \mid 1 \leqq n \leqq 5,n\text{は整数}\}$ (3)2つの集合$A,B$に関して,$A$のすべての要素が$B$の要素でもある場合,つまり$x \in A$ならば$x \in B$が成り立つとき,$A$を$B$の部分集合といい,$A \subset B$と表す.このとき,$A$は$B$に含まれる,あるいは$B$は$A$を含むという.また,$A$は$A$自身の部分集合でもあり,任意の集合$A$について$A \subset A$が成り立つ. 2つの集合$A,B$が一致しているとは,互いに他方の部分集合となっていることである.すなわち, $A \text{ と } B \text{ が等しい } \Longleftrightarrow A \subset B \text { かつ } B \subset A \Longleftrightarrow A=B$ (4)空集合$\varnothing$は,要素を1つも含まない集合を指す.任意の集合$A$に対して,$\varnothing$は$A$の部分集合であるとする.すなわち,$\varnothing \subset A$と約束する. $A,B$の両方に属するような要素全体の集合を$A$と$B$ の共通部分($A$と$B$の交わ り)といい,$A \cap B$で表す. $A,B$の少なくとも一方に属するような要素全体の集合を$A$と$B$の和集合($A$と$B$の結び)といい,$A \cup B$で表す. (5)全体集合とは,特定の文脈や議論において,考えられるすべての要素を含む集合である. 補集合とは,全体集合$U$に属し,かつ$U$の部分集合$A$に属さない要素全体からなる集合である.これを$\overline{A}$で表す($A^c$で表されることもある) また,次のことが成り立つ. $$\overline{\varnothing}=U,\overline{U}=\varnothing,A \cap \overline{A}=\varnothing,A \cup \overline{A}=U,\overline{\overline{A}}=A$$ (6)ド・モルガンの法則(ド・モーガンの法則) $\overline{A \cup B}=\overline{A} \cap \overline{B}$ $\overline{A \cap B}=\overline{A} \cup \overline{B}$
% 基本事項A1.1.2:有限集合の要素の個数(One More)
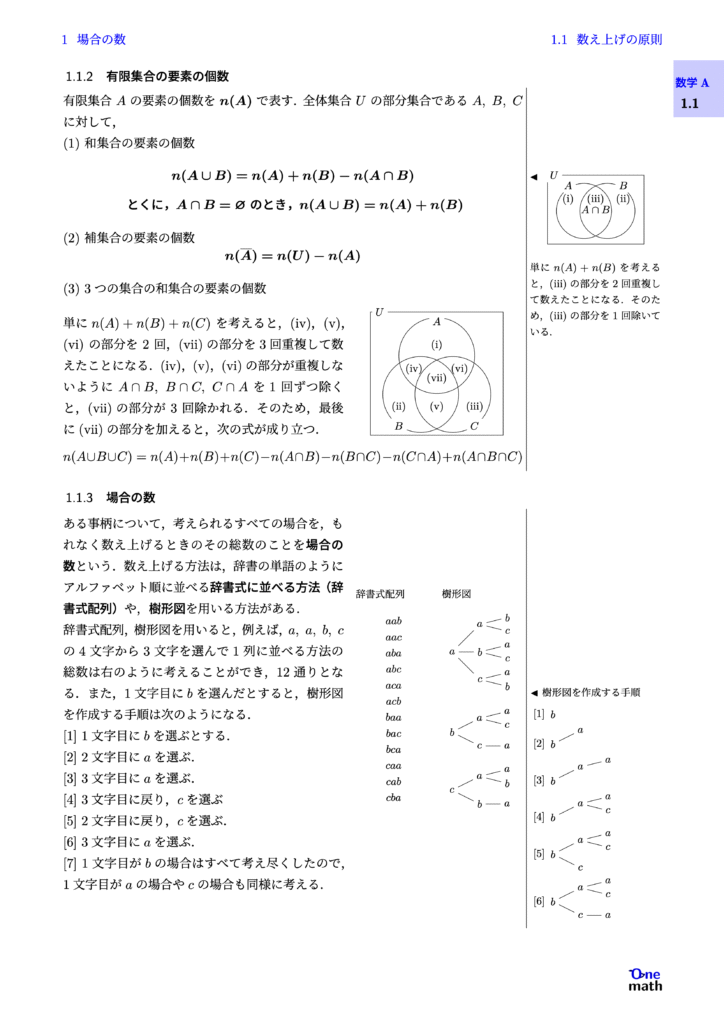
有限集合$A$の要素の個数を$n(A)$で表す.全体集合$U$の部分集合である$A,B,C$に対して, (1)和集合の要素の個数 $$n(A \cup B)=n(A)+n(B)-n(A \cap B)$$ $$\text { とくに,} A \cap B=\varnothing \text { のとき,} n(A \cup B)=n(A)+n(B) $$ (2)補集合の要素の個数 $$ n(\overline{A})=n(U)-n(A) $$ (3)3つの集合の和集合の要素の個数 単に$n(A)+n(B)+n(C)$を考えると,(iv),(v),(vi)の部分を2回,(vii)の部分を3回重複して数えたことになる. (iv),(v),(vi)の部分が重複しないように$A \cap B,B \cap C,C \cap A$を1回ずつ除くと,(vii)の部分が3回除かれる.そのため,最後に(vii)の部分を加えると,次の式が成り立つ. $$n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)$$
% 基本事項A1.1.3:場合の数(One More)
ある事柄について,考えられるすべての場合を,もれなく数え上げるときのその総数のことを場合の数という.数え上げる方法は,辞書の単語のようにアルファベット順に並べる辞書式に並べる方法(辞書式配列)や,樹形図を用いる方法がある. 辞書式配列,樹形図を用いると,例えば,$a,a,b,c$の4文字から3文字を選んで1列に並べる方法の総数は右のように考えることができ,12通りとなる.また,1文字目に$b$を選んだとすると,樹形図を作成する手順は次のようになる. [1]1文字目に$b$を選ぶとする. [2]2文字目に$a$を選ぶ. [3]3文字目に$a$を選ぶ. [4]3文字目に戻り,$c$を選ぶ [5]2文字目に戻り,$c$を選ぶ. [6]3文字目に$a$を選ぶ. [7]1文字目が$b$の場合はすべて考え尽くしたので,1文字目が$a$の場合や$c$の場合も同様に考える. 辞書式配列 $aab$ $aac$ $aba$ $abc$ $aca$ $acb$ $baa$ $bac$ $bca$ $caa$ $cab$ $cba$
% 基本事項A1.1.4:和の法則・積の法則(One More)
(1)和の法則 2つの事柄$A,B$について,$A$である場合が$m$通り,$B$である場合が$n$通りで,$A$と$B$が同時に起こらないとする.このとき,$A$または$B$が起こる場合の数は,$m+n$通りである. つまり,$n(A \cap B)=0$のとき, $$ n(A \cup B)=n(A)+n(B) $$ (2)積の法則 2つの事柄$A,B$について,$A$である場合が$m$通りあり,そのどの場合についても$B$である場合が$n$通りあるとき,$A,B$がともに起こる場合の数は,$m \times n$通りである. (3)自然数$N$が$N=p^aq^br^c\cdots$と素因数分解されているとき, (i)$N$の約数の個数は, $$(a+1)(b+1)(c+1)\cdots (\text{個})$$ (ii)$N$の約数の総和は, $$(1+p+p^2+\cdots +p^a)(1+q+q^2+\cdots +q^b)(1+r+r^2+\cdots +r^c)\cdots$$
% 基本事項A1.2.1:順列(One More)
(1)順列(permutation)$\cdots$異なる$n$個のものから$r$個を取り出して1列に並べる順列の総数は, $ { }_n \mathrm{P}_r $ と表し, $$ { }_n \mathrm{P}_r=\underbrace{n(n-1)(n-2) \cdots (n-r+1)}_{r\text{個の連続する自然数の積}} $$ (2)$n$の階乗を$n!=n(n-1)(n-2) \cdots 3 \cdot 2 \cdot 1$とし,$0!=1$と定める. 階乗の記号を用いると,順列は, $$ { }_n \mathrm{P}_r=\underbrace{n(n-1) \cdots (n-r+1)}_{r \text { 個の連続する自然数の積 }}=\frac{n!}{(n-r)!} $$ また,$n$個のものすべての順列の総数は${ }_n \mathrm{P}_n=n!$であり,${ }_n \mathrm{P}_0=1$と定める.
% 基本事項A1.2.2:円順列と数珠順列(One More)
異なる$n$個の円順列の総数は, $$ \text { 円順列の総数 }=\frac{{ }_n \mathrm{P}_n}{n}=(n-1)! $$ 異なる$n$個の数珠順列の総数は, $$ \text{ 数珠順列の総数} =\frac{\text { 円順列の総数 }}{2}=\frac{{ }_n \mathrm{P}_n}{2 n}=\frac{(n-1) !}{2} (n\geqq 3) $$ なお,裏表があるので,$2$で割ることに注意すること.
% 基本事項A1.2.3:重複順列(One More)
重複順列$\cdots$異なる$n$個のものから重複を許して,$r$個を取り出して並べる順列の総数は,$n^r$
% 基本事項A1.2.4:組合せ(One More)
組合せ(combination)$\cdots$異なる$n$個のものから$r$個取った組合せの総数は ${ }_n \mathrm{C}_r$ と表し,異なる$n$個のものから$r$個とった順列の総数を,異なる$r$個のものから$r$個とった順列の総数で割った値となる.つまり, $${ }_n \mathrm{C}_r=\frac{{ }_n \mathrm{P}_r}{r !}=\frac{n(n-1)(n-2) \cdots (n-r+1)}{r(r-1)(r-2) \cdots 1}=\frac{n !}{r !(n-r) !}$$ また,次の等式が成り立つ. $${ }_n \mathrm{C}_0=1,{ }_n \mathrm{C}_n=1,{ }_n \mathrm{C}_r={ }_n \mathrm{C}_{n-r},{ }_n \mathrm{C}_r={ }_{n-1} \mathrm{C}_{r-1}+{ }_{n-1} \mathrm{C}_r$$
% 基本事項A1.2.5:同じものを含む順列(One More)
同じものを含む順列$\cdots$$n$個のものから,同じものがそれぞれ,$p$個,$q$個,$r$個,$\cdots$あるとき,$n$個のものすべてを1列に並べる順列の総数は, $$\frac{n!}{p!q!r!\cdots} (p+q+r+\cdots=n)$$