% 例題I4.1.2：三角比を用いた測量 （One More）★★
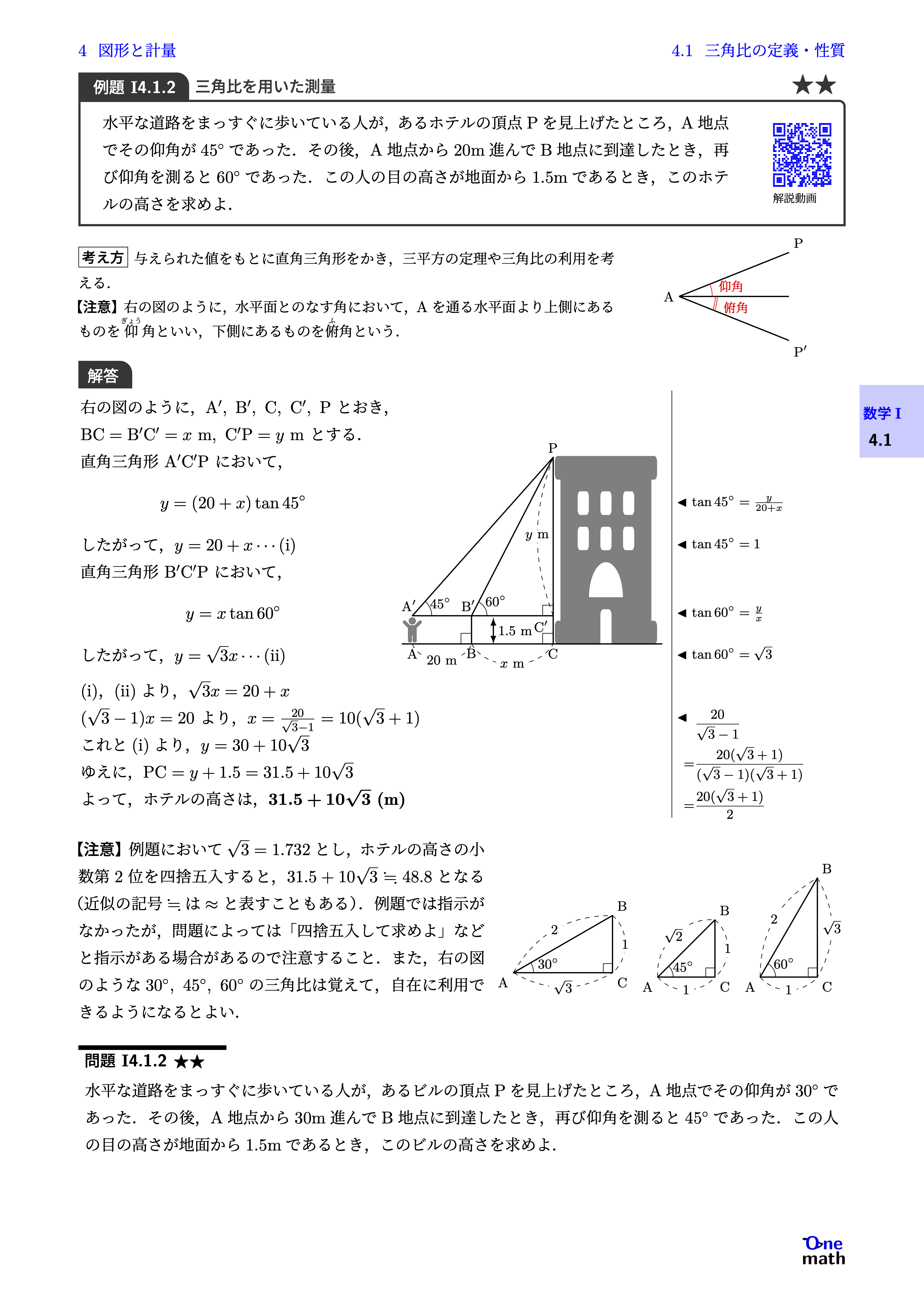
水平な道路をまっすぐに歩いている人が,あるホテルの頂点Pを見上げたところ,A地点でその仰角が$45^{\circ}$であった.その後,A地点から20m進んでB地点に到達したとき,再び仰角を測ると$60^{\circ}$であった.この人の目の高さが地面から1.5mであるとき,このホテルの高さを求めよ.
% 解答（例題I4.1.2）
右の図のように,$\mathrm{A}^{\prime},\mathrm{B}^{\prime},\mathrm{C},\mathrm{C}^\prime,\mathrm{P}$とおき,$\mathrm{BC}=\mathrm{B}^{\prime} \mathrm{C}^{\prime}=x \mathrm{m},\mathrm{C}^{\prime}\mathrm{P}=y \mathrm{m}$とする. 直角三角形$\mathrm{A}^{\prime} \mathrm{C}^{\prime}\mathrm{P}$において,$$y=(20+x)\tan{45}^\circ$$したがって,$y=20+x \cdots (\mathrm{i})$直角三角形$\mathrm{B}^{\prime} \mathrm{C}^{\prime}\mathrm{P}$において,$$y=x\tan 60^{\circ}$$したがって,$y=\sqrt{3} x \cdots (\mathrm{ii})$(i),(ii)より,$\sqrt{3} x=20+x$$(\sqrt{3}-1)x=20$より,$x=\frac{20}{\sqrt{3}-1}=10(\sqrt{3}+1)$これと(i)より,$y=30+10\sqrt{3}$ゆえに,$\mathrm{PC}=y+1.5=31.5+10\sqrt{3}$よって,ホテルの高さは,$31.5+10\sqrt{3} (\mathrm{m})$
% 問題I4.1.2
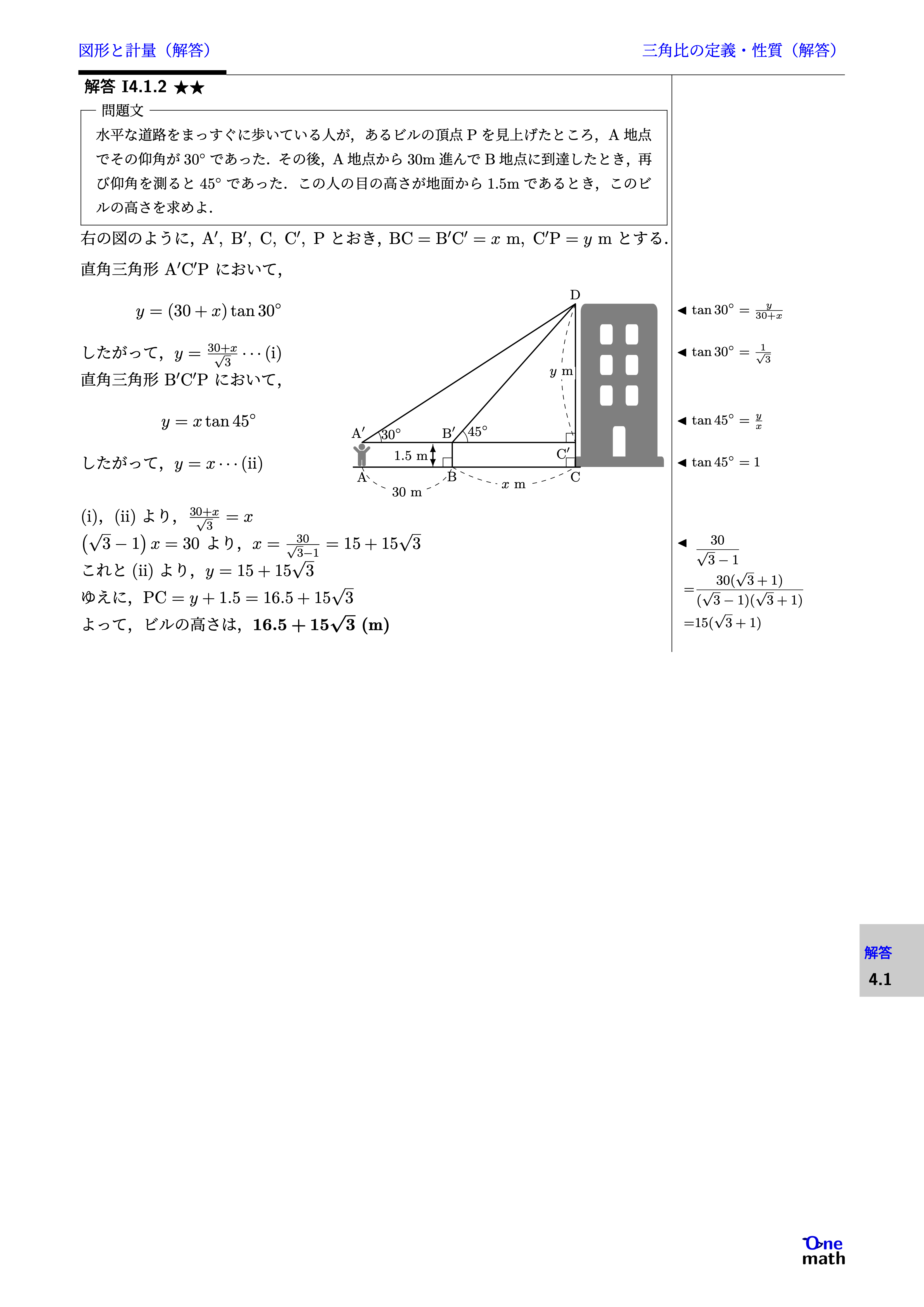
水平な道路をまっすぐに歩いている人が,あるビルの頂点Pを見上げたところ,A地点でその仰角が$30^{\circ}$であった.その後,A地点から30m進んでB地点に到達したとき,再び仰角を測ると$45^{\circ}$であった.この人の目の高さが地面から1.5mであるとき,このビルの高さを求めよ.
% 解答I4.1.2
右の図のように,$\mathrm{A}^{\prime},\mathrm{B}^{\prime},\mathrm{C},\mathrm{C}^\prime,\mathrm{P}$とおき,$\mathrm{BC}=\mathrm{B}^{\prime} \mathrm{C}^{\prime}=x \mathrm{m},\mathrm{C}^{\prime}\mathrm{P}=y \mathrm{m}$とする. 直角三角形$\mathrm{A}^{\prime} \mathrm{C}^{\prime}\mathrm{P}$において,$$y=(30+x)\tan{30}^\circ$$したがって,$y=\frac{30+x}{\sqrt{3}} \cdots (\mathrm{i})$直角三角形$\mathrm{B}^{\prime} \mathrm{C}^{\prime}\mathrm{P}$において,$$y=x\tan 45^{\circ}$$したがって,$y=x \cdots (\mathrm{ii})$(i),(ii)より,$\frac{30+x}{\sqrt{3}}=x$$\left(\sqrt{3}-1\right)x=30$より,$x=\frac{30}{\sqrt{3}-1}=15+15\sqrt{3}$これと(ii)より,$y=15+15\sqrt{3}$ゆえに,$\mathrm{PC}=y+1.5=16.5+15\sqrt{3}$よって,ビルの高さは,$16.5+15\sqrt{3} (\mathrm{m})$
