% 例題I4.1.3：$15^\circ$の三角比 （One More）★★★
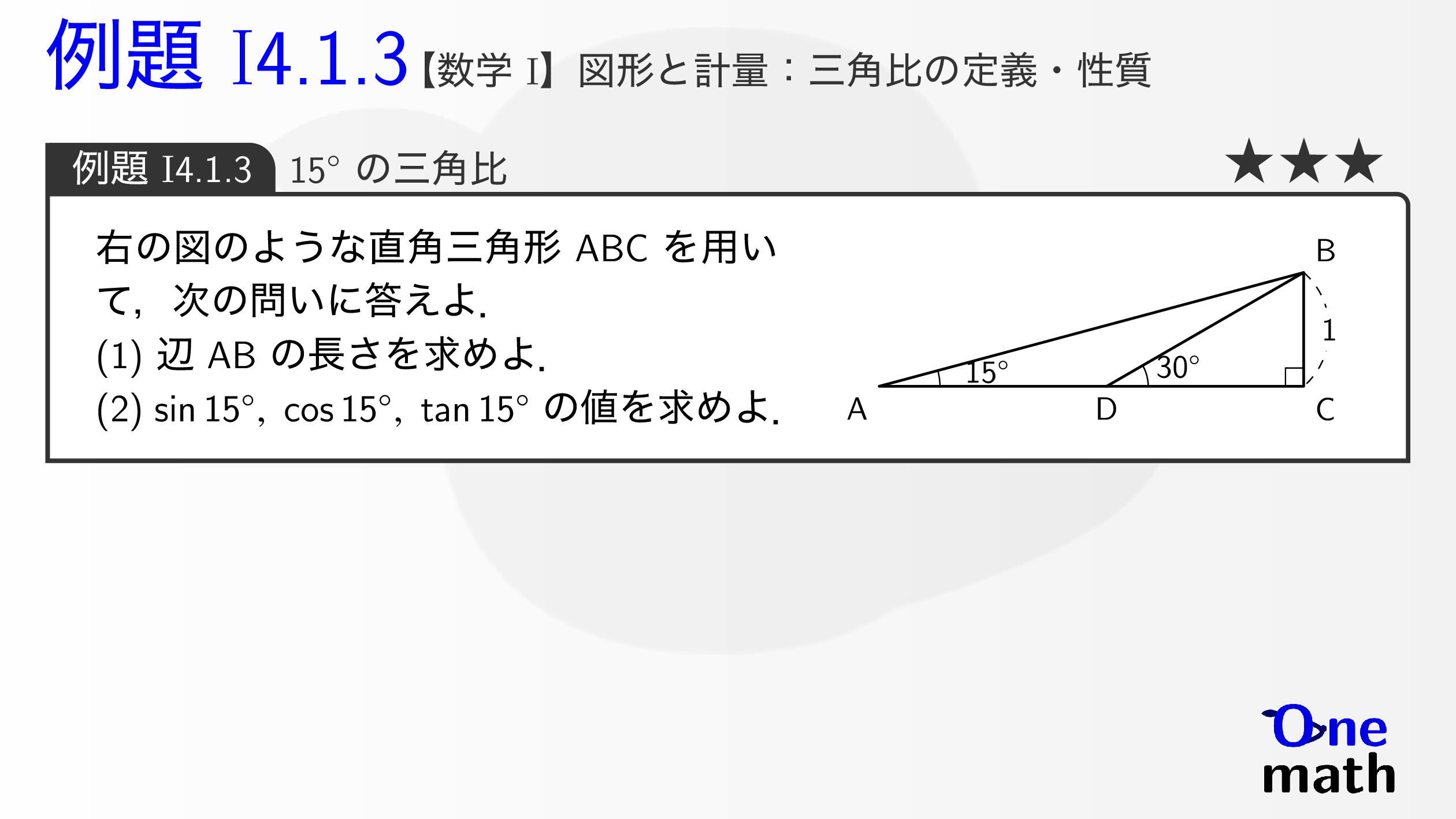
右の図のような直角三角形ABCを用いて,次の問いに答えよ. (1)辺ABの長さを求めよ. (2)$\sin 15^{\circ},\cos 15^{\circ},\tan 15^{\circ}$の値を求めよ.
% 解答（例題I4.1.3）
(1)$\angle \mathrm{CBD}=180^\circ-(90^\circ+30^{\circ})=60^\circ$より,$\mathrm{CD=\sqrt{3},\mathrm{BD}=2 }$また,$\angle \mathrm{ABC}=180^{\circ}-(90^\circ+15^{\circ})=75^{\circ}$より,$\angle \mathrm{ABD}=75^{\circ}-60^{\circ}=15^{\circ}$したがって,$\triangle \mathrm{ABD}$は$\mathrm{AD}=\mathrm{BD}$の二等辺三角形である. ゆえに,$\mathrm{CD}=\sqrt{3}$より,$\mathrm{AC}=\mathrm{AD}+\mathrm{CD}=2+\sqrt{3} \cdots (\mathrm{i})$$\triangle \mathrm{ABC}$において,三平方の定理より,$$\mathrm{AB}^2=(2+\sqrt{3})^2+1^2=8+4\sqrt{3}$$よって,$\mathrm{AB}>0$より,$$\mathrm{AB}=\sqrt{8+4\sqrt{3}} =\sqrt{8+2\sqrt{12}}=\sqrt{6}+\sqrt{2} \cdots (\mathrm{ii})$$(2)$\triangle \mathrm{ABC}$において,(i),(ii),$\mathrm{BC}=1$より,$$\begin{aligned} & \sin 15^{\circ}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{6}+\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})}=\frac{\sqrt{6}-\sqrt{2}}{4} \\ & \cos 15^{\circ}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{2+\sqrt{3}}{\sqrt{6}+\sqrt{2}}=\frac{(2+\sqrt{3})(\sqrt{6}-\sqrt{2})}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})}=\frac{\sqrt{6}+\sqrt{2}}{4}\\ & \tan 15^{\circ}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{1}{2+\sqrt{3}}=\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}=2-\sqrt{3} \end{aligned}$$
% 問題I4.1.3
二等辺三角形ABCにおいて$\mathrm{AB}=\mathrm{AC},\mathrm{BC}=1,\angle \mathrm{A}=36^{\circ}$とし,$\angle \mathrm{B}$の二等分線と辺ACの交点をDとするとき,次の値を求めよ. (1)辺BDの長さ (2)辺ABの長さ (3)$\sin 18^{\circ}$
% 解答I4.1.3
(1)$\triangle \mathrm{ABC}$は二等辺三角形であり,$\angle \mathrm{A}=36^{\circ}$であるから,$$\angle \mathrm{B}=\angle \mathrm{C}=\frac{180^{\circ}-36^{\circ}}{2}=72^{\circ}$$BDは$\angle \mathrm{B}$の二等分線であるから,$$\angle \mathrm{ABD}=\angle \mathrm{CBD}=36^{\circ}$$また,$\angle \mathrm{BCD}=\angle \mathrm{BDC}=72^{\circ}$であるから,$\triangle \mathrm{BCD}$は$\mathrm{BC}=\mathrm{BD}$の二等辺三角形である. よって,$\mathrm{BD}=\mathrm{BC}=1$(2)$\triangle \mathrm{DAB}$は$\mathrm{DA}=\mathrm{DB}$を満たす二等辺三角形であるから,$\mathrm{AD}=1$$\mathrm{AB}=x$とすると,$\mathrm{CD}=x-1$$\triangle \mathrm{ABC} \backsim \triangle \mathrm{BCD}$であるから,$\mathrm{AB}:\mathrm{BC}=\mathrm{BC}:\mathrm{CD}$, すなわち,$x:1=1:(x-1)$したがって,$x(x-1)=1$整理すると,$x^2-x-1=0$これを解くと,$x>0$より ,$x=\frac{1+\sqrt{5}}{2}$よって,$\mathrm{AB}=\frac{1+\sqrt{5}}{2}$(3)$$\sin 18^{\circ}=\frac{\frac{1}{2} \mathrm{BC}}{\mathrm{AB}}=\frac{1}{2x}=\frac{1}{\sqrt{5}+1} =\frac{\sqrt{5}-1}{(\sqrt{5}+1)(\sqrt{5}-1)}=\frac{\sqrt{5}-1}{4}$$
