% 例題I4.1.6：三角比を含む方程式1 （One More）★
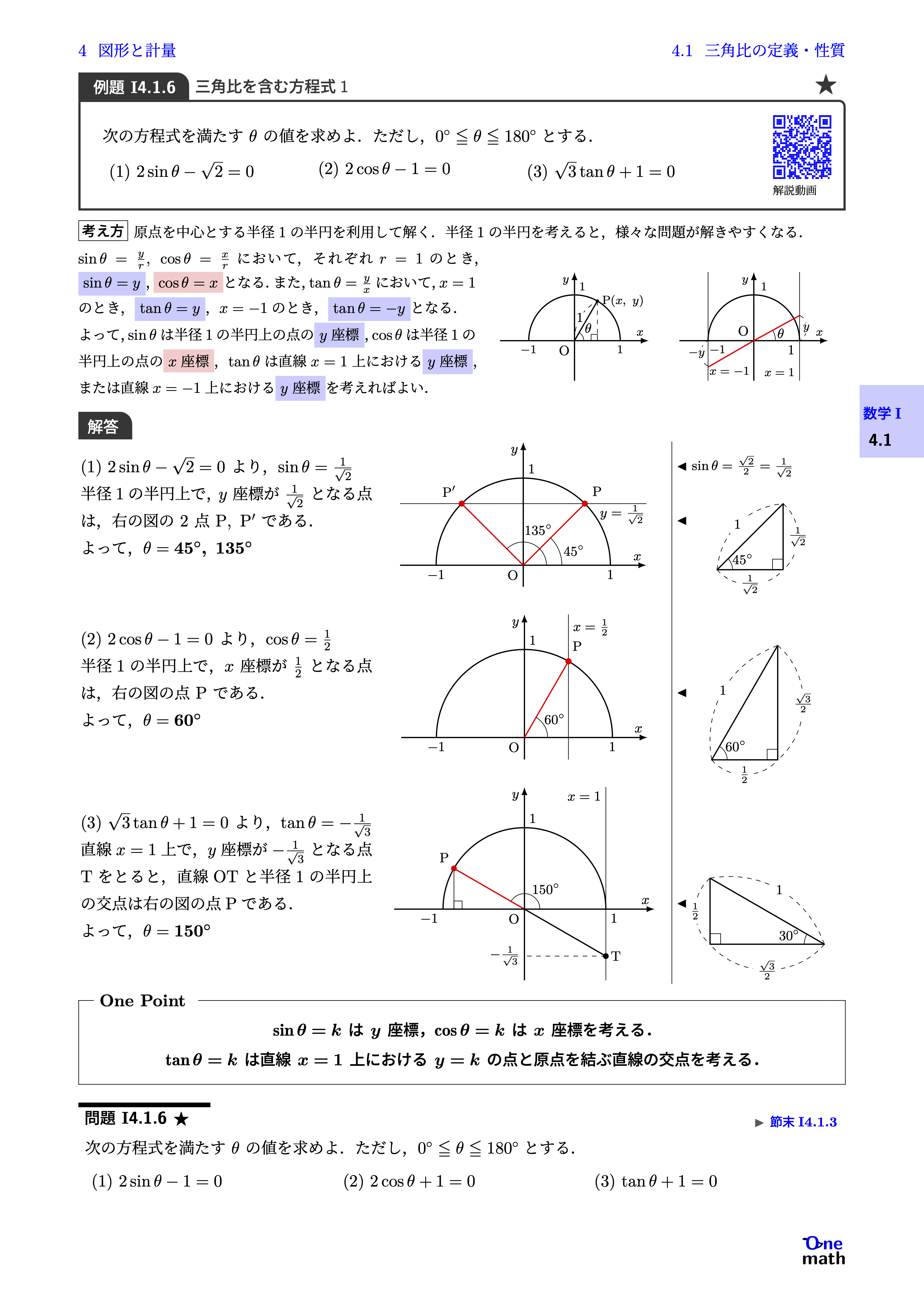
次の方程式を満たす$\theta$の値を求めよ.ただし,$0^{\circ} \leqq \theta \leqq 180^{\circ}$とする. (1)$2 \sin \theta-\sqrt{2}=0$(2)$2 \cos \theta-1=0$(3)$\sqrt{3}\tan \theta+1=0$
% 解答（例題I4.1.6）
(1)$2 \sin \theta-\sqrt{2}=0$より,$\sin \theta=\frac{1}{\sqrt{2}}$半径1の半円上で,$y$座標が$\frac{1}{\sqrt{2}}$となる点は,右の図の2点$\mathrm{P},\mathrm{P}^{\prime}$である. よって,$\theta=45^{\circ},135^{\circ}$(2)$2 \cos \theta-1=0$より,$\cos \theta=\frac{1}{2}$半径1の半円上で,$x$座標が$\frac{1}{2}$となる点は,右の図の点$\mathrm{P}$である. よって,$\theta=60^{\circ}$(3)$\sqrt{3}\tan \theta+1=0$より,$\tan \theta=-\frac{1}{\sqrt{3}}$直線$x=1$上で,$y$座標が$-\frac{1}{\sqrt{3}}$となる点Tをとると,直線OTと半径1の半円上の交点は右の図の点Pである. よって,$\theta=150^{\circ}$
% 問題I4.1.6
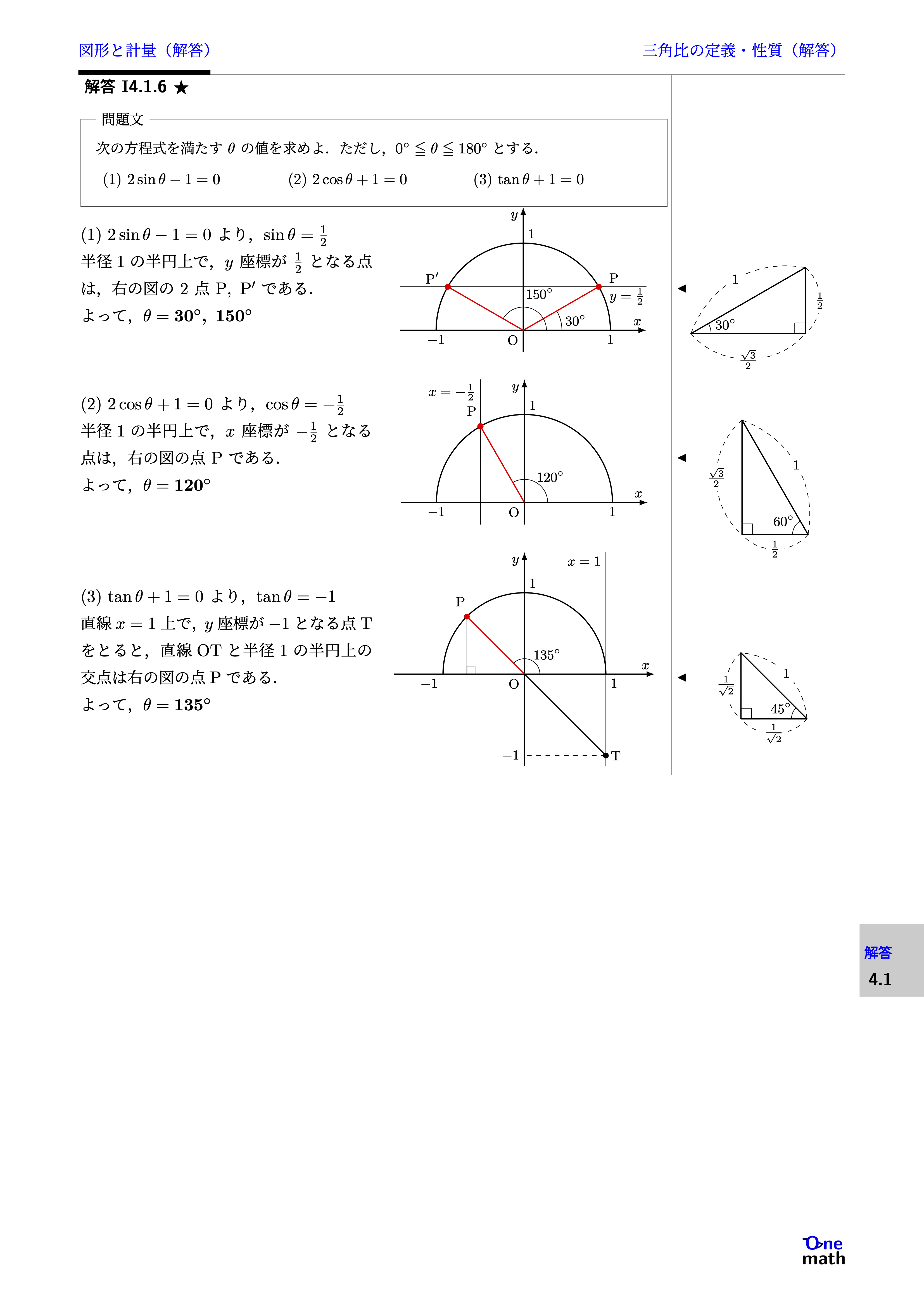
次の方程式を満たす$\theta$の値を求めよ.ただし,$0^{\circ} \leqq \theta \leqq 180^{\circ}$とする. (1)$2 \sin \theta-1=0$(2)$2\cos \theta+1=0$(3)$\tan \theta+1=0$
% 解答I4.1.6
(1)$2 \sin \theta-1=0$より,$\sin \theta=\frac{1}{2}$半径1の半円上で,$y$座標が$\frac{1}{2}$となる点は,右の図の2点$\mathrm{P},\mathrm{P}^{\prime}$である. よって,$\theta=30^{\circ},150^{\circ}$(2)$2\cos \theta+1=0$より,$\cos \theta=-\frac{1}{2}$半径1の半円上で,$x$座標が$-\frac{1}{2}$となる点は,右の図の点$\mathrm{P}$である. よって,$\theta=120^{\circ}$(3)$\tan \theta+1=0$より,$\tan \theta=-1$直線$x=1$上で,$y$座標が$-1$となる点Tをとると,直線OTと半径1の半円上の交点は右の図の点Pである. よって,$\theta=135^{\circ}$
