% 例題I1.3.4:不等式を満たす整数の解 (One More)★★
(1)不等式$4x-2<2x+4$を満たす自然数$x$の値をすべて求めよ. (2)不等式$4x+a<5x<3x+10$を満たす整数$x$がちょうど2個存在するような定数$a$の値の範囲を求めよ.
% 解答(例題I1.3.4)
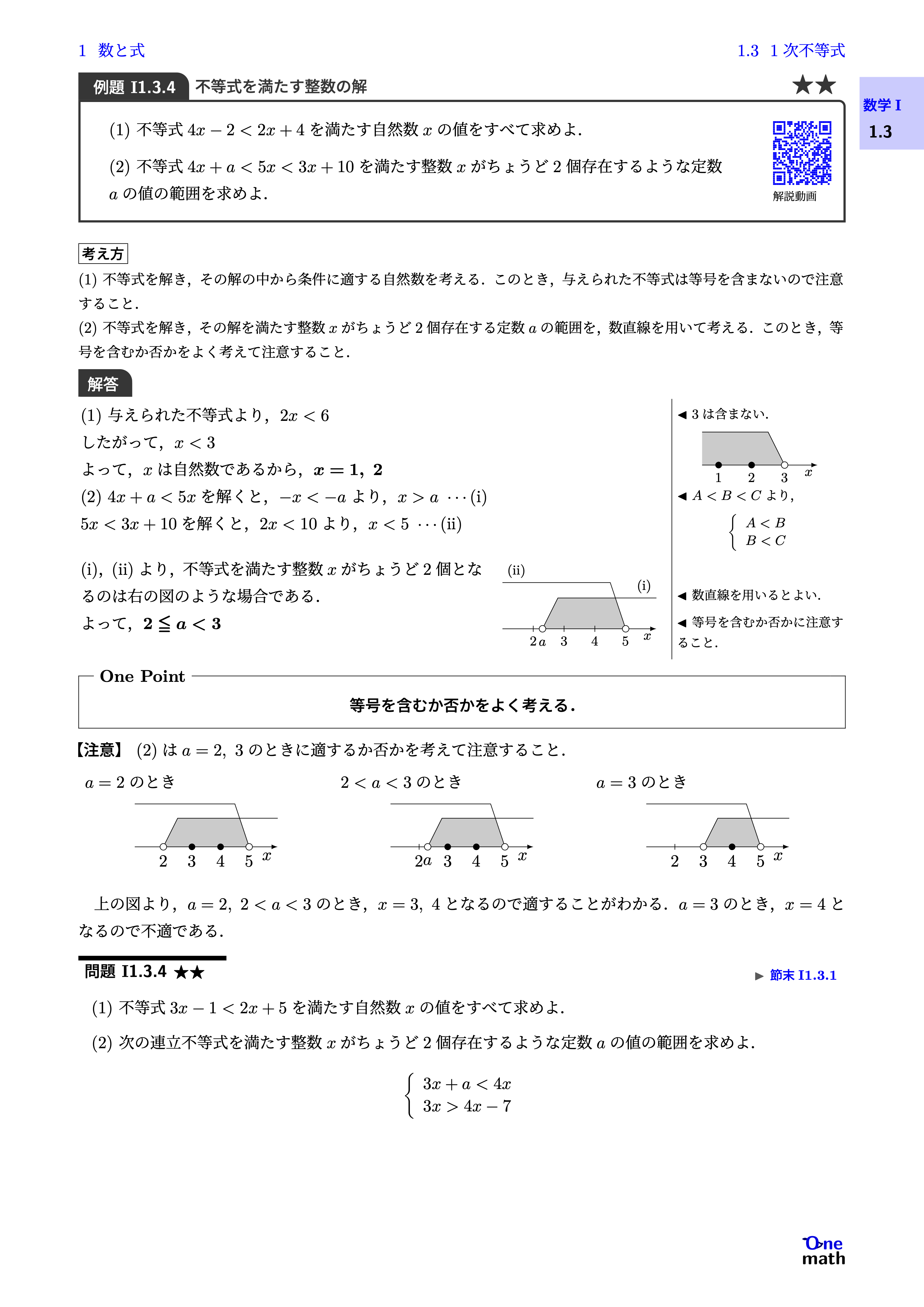
(1)与えられた不等式より,$2x<6$したがって,$x<3$よって,$x$は自然数であるから,$x=1,2$(2)$4x+a<5x$を解くと,$-x<-a$より,$x>a \cdots (\mathrm{i})$5x<3x+10$を解くと,$2x<10$より,$x<5 \cdots (\mathrm{ii})$(i),(ii)より,不等式を満たす整数$x$がちょうど2個となるのは右の図のような場合である. よって,$2 \leqq a<3$
% 問題I1.3.4
(1)不等式$3x-1<2x+5$を満たす自然数$x$の値をすべて求めよ. (2)次の連立不等式を満たす整数$x$がちょうど2個存在するような定数$a$の値の範囲を求めよ.$\left\{\begin{array}{l} 3x+a<4x \\ 3x>4x-7 \end{array}\right.$
% 解答I1.3.4
(1)与えられた不等式より,$x<6$したがって,$x$は自然数であるから,$x=1,2,3,4,5$(2)$3x+a<4x$を解くと,$-x<-a$より,$x>a \cdots (\mathrm{i})$3x>4x-7$を解くと,$-x>-7$より,$x<7 \cdots (\mathrm{ii})$(i),(ii)より,不等式を満たす整数$x$がちょうど2個となるのは右の図のような場合である. よって,$4 \leqq a<5$