% 例題I3.1.12:絶対値記号を含む関数のグラフ3 (One More)★★★
不等式$|2x+2|+|x-1|>-x+2$をグラフを利用して解け.
% 解答(例題I3.1.12)
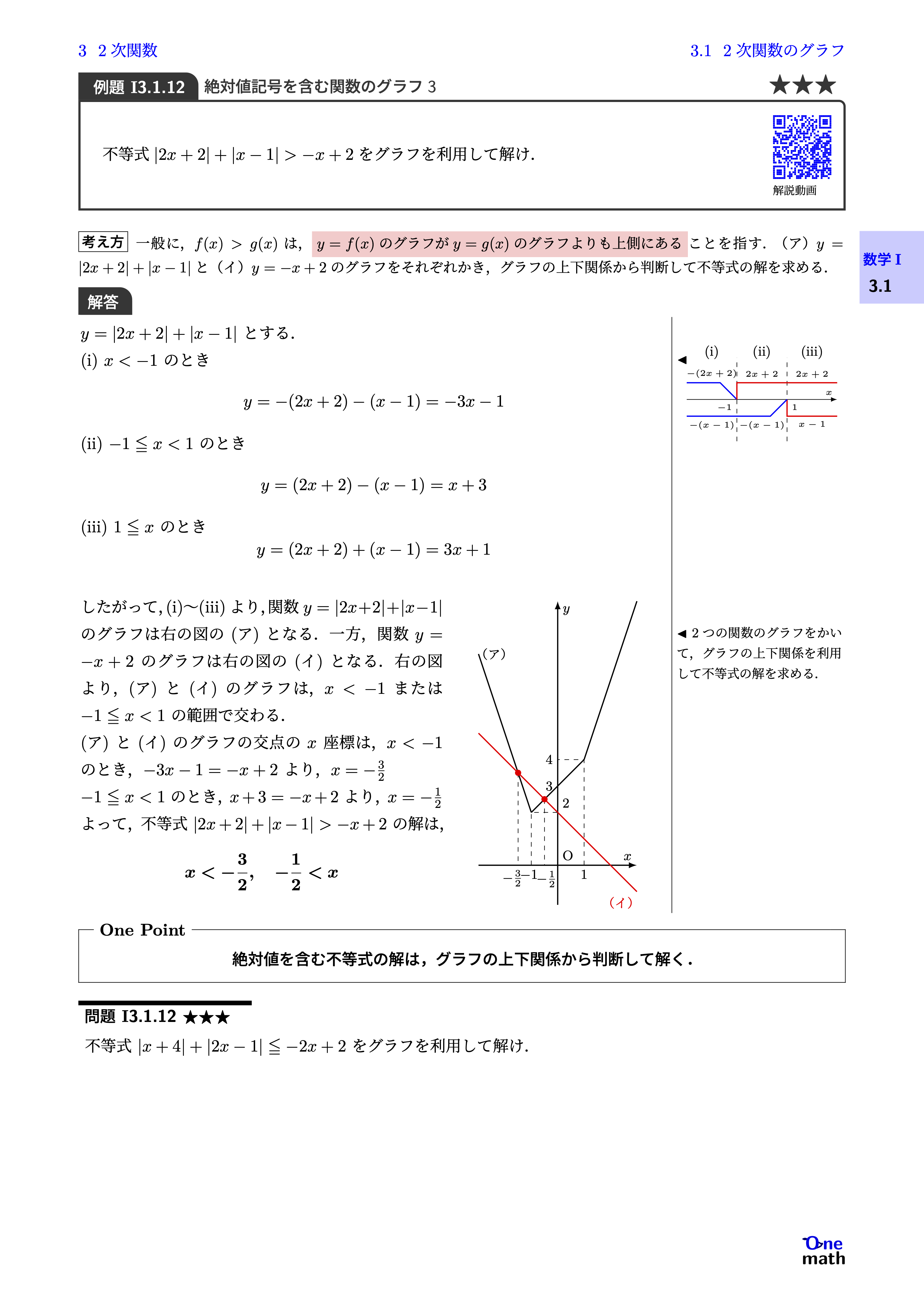
$y=|2x+2|+|x-1|$とする. (i)$x<-1$のとき$$y=-(2x+2)-(x-1)=-3x-1$$(ii)$-1 \leqq x<1$のとき$$y=(2x+2)-(x-1)=x+3$$(iii)$1 \leqq x$のとき$$y=(2x+2)+(x-1)=3x+1$$したがって,(i)〜(iii)より,関数$y=|2x+2|+|x-1|$のグラフは右の図の(ア)となる.一方,関数$y=-x+2$のグラフは右の図の(イ)となる.右の図より,(ア)と(イ)のグラフは,$x<-1$または$-1 \leqq x<1$の範囲で交わる. (ア)と(イ)のグラフの交点の$x$座標は,$x<-1$のとき,$-3x-1=-x+2$より,$x=-\frac{3}{2}$$-1 \leqq x<1$のとき,$x+3=-x+2$より,$x=-\frac{1}{2}$よって,不等式$|2x+2|+|x-1|>-x+2$の解は,$$x<-\frac{3}{2},-\frac{1}{2}<x$$
% 問題I3.1.12
不等式$|x+4|+|2x-1| \leqq -2x+2$をグラフを利用して解け.
% 解答I3.1.12
$y=|x+4|+|2x-1|$とおく. (i)$x<-4$のとき$$y=-(x+4)-(2x-1) =-3x-3$$(ii)$-4 \leqq x<\frac{1}{2}$のとき$$y=(x+4)-(2x-1) =-x+5$$(iii)$\frac{1}{2} \leqq x$のとき$$y=(x+4)+(2x-1) =3x+3$$したがって,(i)〜(iii)より,関数$y=|x+4|+|2x-1|$のグラフは右の図の(ア)となる. 一方,関数$y=-2x+2$のグラフは右の図の(イ)となる. 右の図より,(ア)と(イ)のグラフは,$x<-4$または$-4 \leqq x<\frac{1}{2}$の範囲で交わる. (ア)と(イ)のグラフの交点の$x$座標は,$x<-4$のとき,$-3x-3=-2x+2$より,$x=-5$$-4 \leqq x<\frac{1}{2}$のとき,$-x+5=-2x+2$より,$x=-3$よって,不等式$|x+4|+|2x-1| \leqq -2x+2$の解は,$$-5 \leqq x \leqq -3$$