% 例題I3.1.3:値域から1次関数の係数決定 (One More)★
関数$y=ax+b (1 \leqq x \leqq 4)$の最大値が10,最小値が4のとき,定数$a,b$の値を求めよ.
% 解答(例題I3.1.3)
(i)$a>0$のとき グラフは右の図のようになり, \begin{center}$x=1$のとき,最小値4,$x=4$のとき,最大値10 \end{center} をとるから,$$\begin{aligned} & \left\{ \begin{array}{l} a \cdot 1+b=4 \\ a \cdot 4+b=10 \end{array} \right.\\ \end{aligned}$$したがって,$a=2,b=2$これは,$a>0$を満たす. (ii)$a=0$のとき$y=b$(定数関数)となり,最大値と最小値は一致するので,不適である. (iii)$a<0$のとき グラフは右の図のようになり, \begin{center}$x=1$のとき,最大値10,$x=4$のとき,最小値4 \end{center} をとるから,$$\left\{ \begin{array}{l} a \cdot 1+b=10 \\ a \cdot 4+b=4 \end{array} \right.$$したがって,$a=-2,b=12$これは,$a<0$を満たす. よって,(i)〜(iii)より,求める$a,b$の値は,$(a,b)=(2,2),(-2,12)$
% 問題I3.1.3
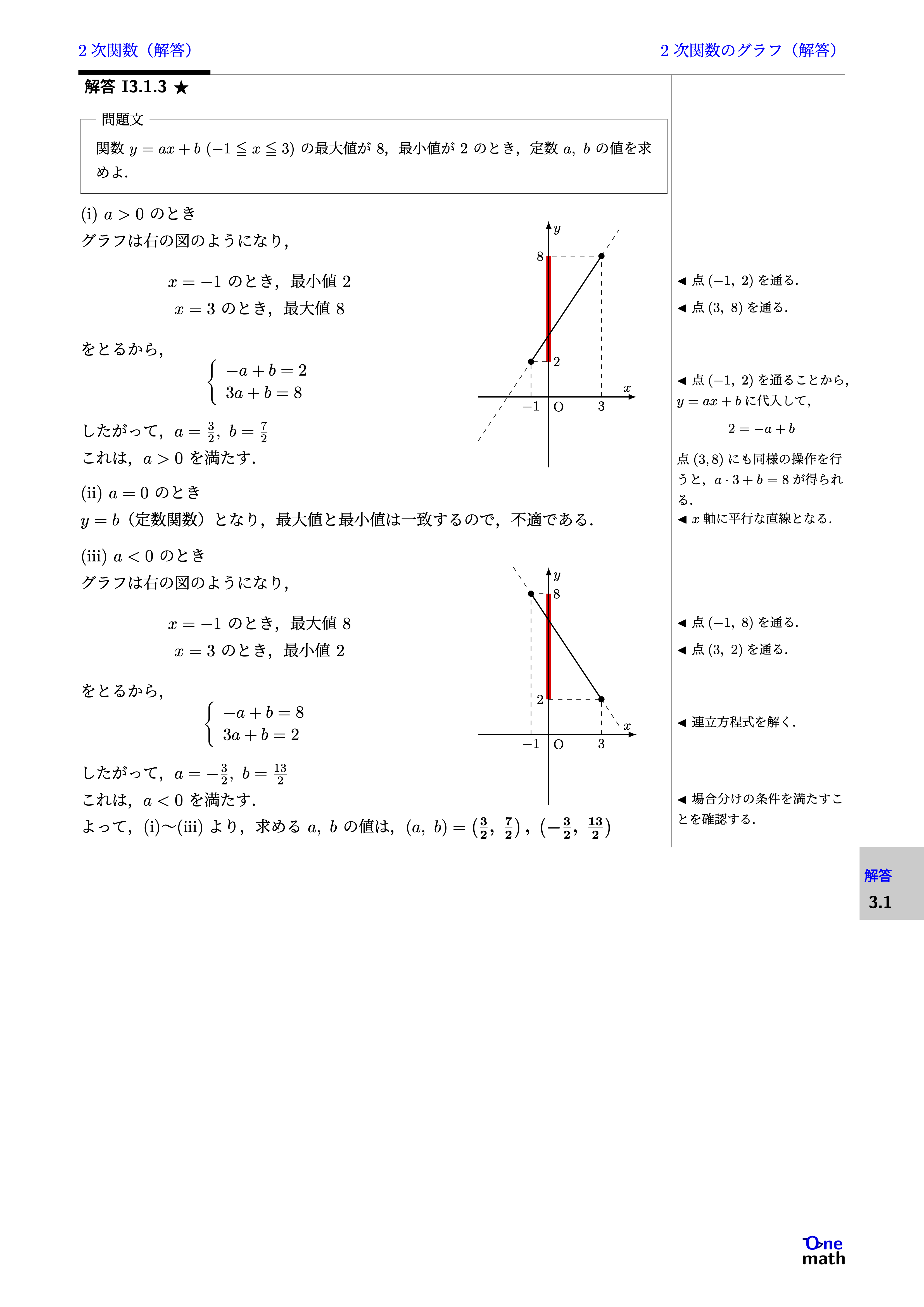
関数$y=ax+b (-1 \leqq x \leqq 3)$の最大値が8,最小値が2のとき,定数$a,b$の値を求めよ.
% 解答I3.1.3
(i)$a>0$のとき グラフは右の図のようになり, \begin{center}$x=-1$のとき,最小値2$x=3$のとき,最大値8 \end{center} をとるから,$$\begin{aligned} & \left\{ \begin{array}{l} -a+b=2 \\ 3a+b=8 \end{array} \right.\\ \end{aligned}$$したがって,$a=\frac{3}{2},b=\frac{7}{2}$これは,$a>0$を満たす. (ii)$a=0$のとき$y=b$(定数関数)となり,最大値と最小値は一致するので,不適である. (iii)$a<0$のとき グラフは右の図のようになり, \begin{center}$x=-1$のとき,最大値8$x=3$のとき,最小値2 \end{center} をとるから,$$\left\{ \begin{array}{l} -a+b=8 \\ 3a+b=2 \end{array} \right.$$したがって,$a=-\frac{3}{2},b=\frac{13}{2}$これは,$a<0$を満たす. よって,(i)〜(iii)より,求める$a,b$の値は,$(a,b)=\left(\frac{3}{2},\frac{7}{2}\right),\left(-\frac{3}{2},\frac{13}{2}\right)$