% 例題I3.1.8:2次関数のグラフの対称移動 (One More)★
放物線$y=x^2-2 x+3$を,次のように移動した放物線の方程式を求めよ. (1)$x$軸に関して対称移動 (2)$y$軸に関して対称移動 (3)原点に関して対称移動
% 解答(例題I3.1.8)
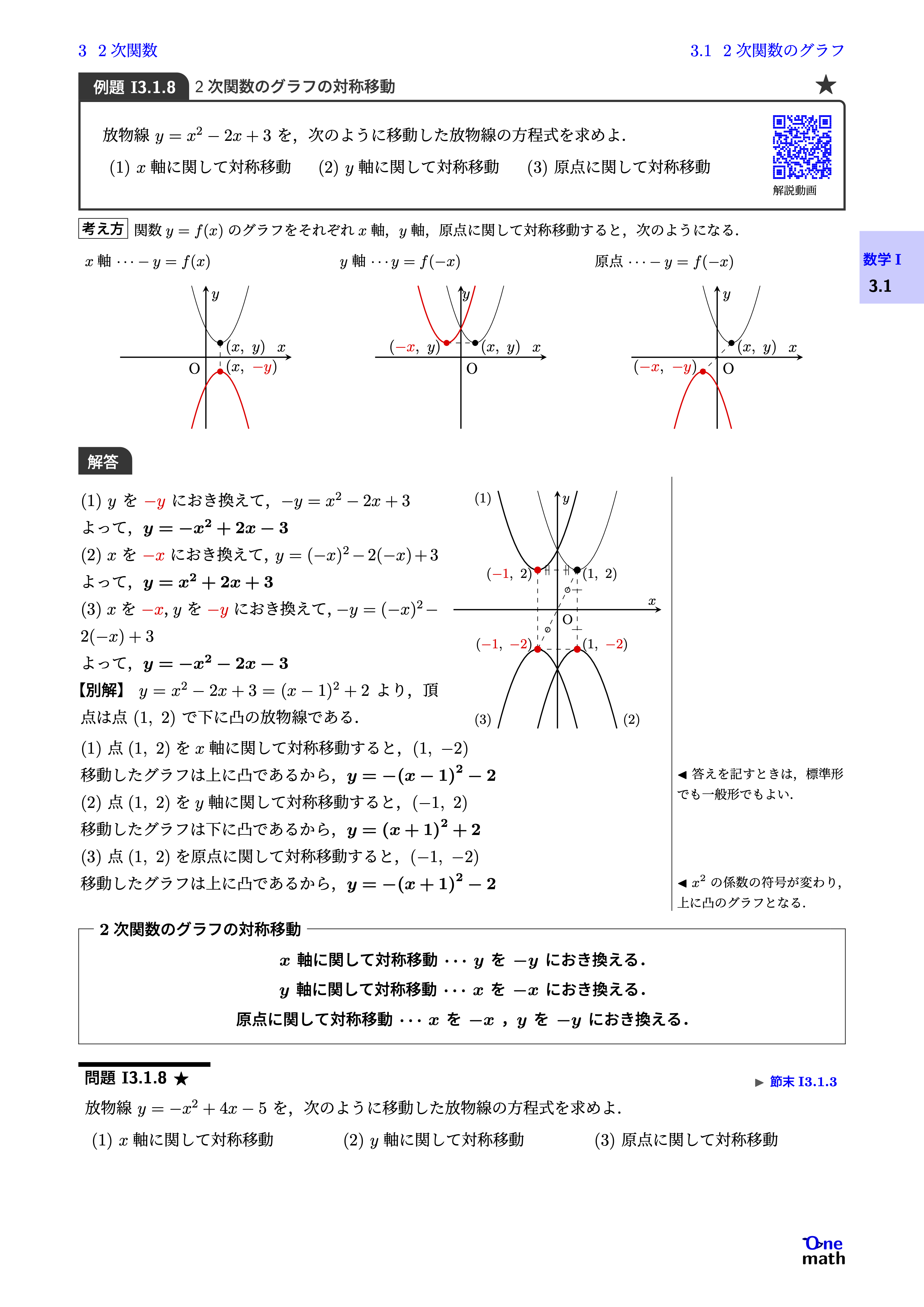
(1)$y$を$-y$におき換えて,$-y=x^2-2 x+3$よって,$y=-x^2+2 x-3$(2)$x$を$-x$におき換えて,$y=(-x)^2-2(-x)+3$よって,$y=x^2+2 x+3$(3)$x$を$-x,y$を$-y$におき換えて,$-y=(-x)^2-2(-x)+3$よって,$y=-x^2-2 x-3$別解:$y=x^2-2 x+3=(x-1)^2+2$より,頂点は点$(1,2)$で下に凸の放物線である. (1)点$(1,2)$を$x$軸に関して対称移動すると,$(1,-2)$移動したグラフは上に凸であるから,$y=-(x-1)^2-2$(2)点$(1,2)$を$y$軸に関して対称移動すると,$(-1,2)$移動したグラフは下に凸であるから,$y=(x+1)^2+2$(3)点$(1,2)$を原点に関して対称移動すると,$(-1,-2)$移動したグラフは上に凸であるから,$y=-(x+1)^2-2$
% 問題I3.1.8
放物線$y=-x^2+4x-5$を,次のように移動した放物線の方程式を求めよ. (1)$x$軸に関して対称移動 (2)$y$軸に関して対称移動 (3)原点に関して対称移動
% 解答I3.1.8
(1)$y$を$-y$におき換えて,$-y=-x^2+4x-5$よって,$y=x^2-4x+5$(2)$x$を$-x$におき換えて,$y=-(-x)^2+4(-x)-5$よって,$y=-x^2-4x-5$(3)$x$を$-x,y$を$-y$におき換えて,$-y=-(-x)^2+4(-x)-5$よって,$y=x^2+4x+5$別解:$y=-x^2+4x-5=-(x-2)^2-1$より,頂点は点$(2,-1)$で上に凸の放物線である. (1)点$(2,-1)$を$x$軸に関して対称移動すると,$(2,1)$移動したグラフは下に凸であるから,$y=(x-2)^2+1$(2)点$(2,-1)$を$y$軸に関して対称移動すると,$(-2,-1)$移動したグラフは上に凸であるから,$y=-(x+2)^2-1$(3)点$(2,-1)$を原点に関して対称移動すると,$(-2,1)$移動したグラフは下に凸であるから,$y=(x+2)^2+1$