% 例題I3.2.6:定義域が変化するときの最大・最小 (One More)★★★
関数$f(x)=x^2-2 x+3(a \leqq x \leqq a+2)$について,$f(x)$の最大値を求めよ.
% 解答(例題I3.2.6)
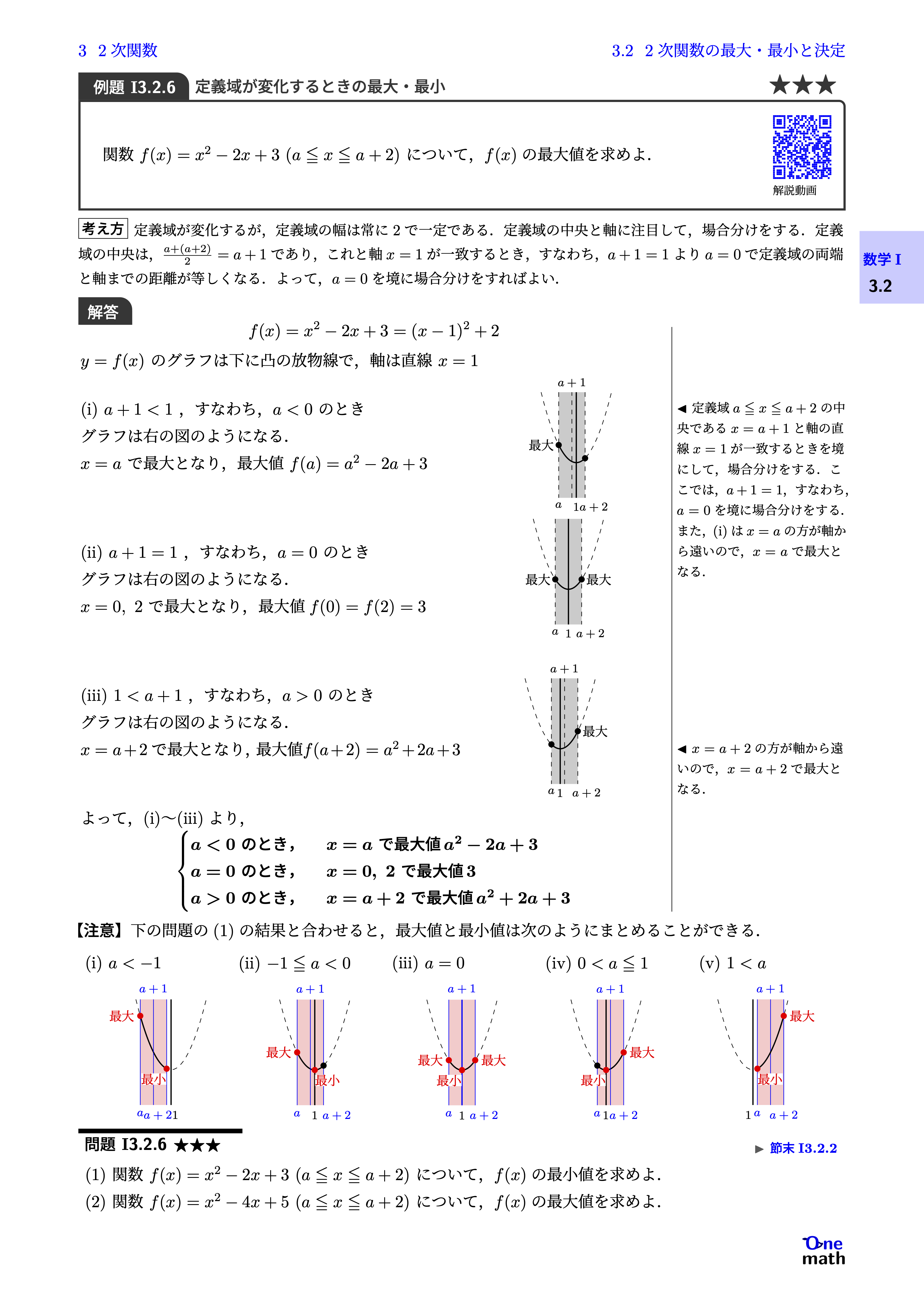
$$f(x)=x^2-2 x+3=(x-1)^2+2$$$y=f(x)$のグラフは下に凸の放物線で,軸は直線$x=1$(i)$a+1<1$,すなわち,$a<0$のとき グラフは右の図のようになる.$x=a$で 最大となり, 最大値$f(a)=a^2-2 a+3$(ii)$a+1=1$,すなわち,$a=0$のとき グラフは右の図のようになる.$x=0,2$で最大となり, 最大値$f(0)=f(2)=3$(iii)$1<a+1$,すなわち,$a>0$のとき グラフは右の図のようになる.$x=a+2$で最大となり,最大値$f(a+2)=a^2+2 a+3$よって,(i)〜(iii)より,$$\begin{cases} a<0 \text{ のとき,} & x=a \text{ で最大値 } a^2-2 a+3 \\ a=0 \text{ のとき,} & x=0,2 \text{ で最大値 } 3 \\ a>0 \text{ のとき,} & x=a+2 \text{ で最大値 } a^2+2 a+3\end{cases}$$
% 問題I3.2.6
(1)関数$f(x)=x^2-2 x+3(a \leqq x \leqq a+2)$について,$f(x)$の最小値を求めよ. (2)関数$f(x)=x^2-4x+5(a \leqq x \leqq a+2)$について,$f(x)$の最大値を求めよ.
% 解答I3.2.6
(1)$f(x)=x^2-2 x+3=(x-1)^2+2$$y=f(x)$のグラフは下に凸の放物線で,軸は直線$x=1$(i)$a+2<1$,すなわち,$a<-1$のとき グラフは右の図のようになる.$x=a+2$で 最小となり, 最小値$f(a+2)=a^2+2 a+3$(ii)$a \leqq 1 \leqq a+2$,すなわち,$-1 \leqq a \leqq 1$のとき グラフは右の図のようになる.$x=1$で最小となり, 最小値$f(1)=2$(iii)$1<a$のとき グラフは右の図のようになる.$x=a$で最小となり,最小値$f(a)=a^2-2 a+3$よって,(i)〜(iii)より,$$\begin{cases} a<-1 \text{ のとき,} & x=a+2 \text{ で最小値 } a^2+2 a+3 \\ -1 \leqq a \leqq 1 \text{ のとき,} & x=1 \text{ で最小値 } 2 \\ 1<a \text{ のとき,} & x=a \text{ で最小値 } a^2-2 a+3\end{cases}$$(2)$f(x)=x^2-4x+5=(x-2)^2+1$$y=f(x)$のグラフは下に凸の放物線で,軸は直線$x=2$(i)$a+1<2$,すなわち,$a<1$のとき グラフは右の図のようになる.$x=a$で 最大となり, 最大値$f(a)=a^2-4a+5$(ii)$a+1=2$,すなわち,$a=1$のとき グラフは右の図のようになる.$x=1,3$で最大となり, 最大値$f(1)=f(3)=2$(iii)$2<a+1$,すなわち,$a>1$のとき グラフは右の図のようになる.$x=a+2$で最大となり,最大値$f(a+2)=a^2+1$よって,(i)〜(iii)より,$$\begin{cases} a<1 \text{ のとき,} & x=a \text{ で最大値 } a^2-4a+5 \\ a=1 \text{ のとき,} & x=1,3 \text{ で最大値 } 2 \\ a>1 \text{ のとき,} & x=a+2 \text{ で最大値 } a^2+1\end{cases}$$