% 例題I3.3.15:放物線と直線の共有点の座標2 (One More)★★
次の放物線と直線の共有点の個数を調べよ.ただし,$k$を定数とする. (1)放物線$y=3x^2+6x+4$,直線$y=-3x+k$(2)放物線$y=x^2-2kx+k^2+5$,直線$y=2x+2$
% 解答(例題I3.3.15)
(1)$\left\{\begin{array}{l}y=3x^2+6x+4 \cdots (\mathrm{i})\\ y=-3x+k \cdots (\mathrm{ii})\end{array}\right.$とする. (i)と(ii)から$y$を消去すると,$3x^2+6x+4=-3x+k$整理すると,$3x^2+9x+4-k=0$この2次方程式の判別式を$D$とすると,$D=9^2-4 \cdot 3 \cdot (4-k)=81-12(4-k)=12k+33$よって,共有点の個数は,$k$の値によって次のようになる.$\begin{alignedat}{2} &12k+33>0 \text{ のとき,すなわち,} k>-\frac{11}{4} \text{ のとき,}&&\text{ 2個}\\ &12k+33=0 \text{ のとき,すなわち,} k=-\frac{11}{4} \text{ のとき,}&&\text{ 1個}\\ &12k+33<0 \text{ のとき,すなわち,} k<-\frac{11}{4} \text{ のとき,}&&\text{ 0個}\\ \end{alignedat}$(2)$\left\{\begin{array}{l}y=x^2-2kx+k^2+5 \cdots (\mathrm{i})\\ y=2x+2 \cdots (\mathrm{ii})\end{array}\right.$とする. (i)と(ii)から$y$を消去すると,$x^2-2kx+k^2+5=2x+2$整理すると,$x^2-2(k+1)x+(k^2+3)=0$この2次方程式の判別式を$D$とすると,$\frac{D}{4}=\{-(k+1)\}^2-1 \cdot (k^2+3)=2k-2$よって,共有点の個数は,$k$の値によって次のようになる.$\begin{alignedat}{2} &2k-2>0 \text{ のとき,すなわち,} k>1 \text{ のとき,}&&\text{ 2個}\\ &2k-2=0 \text{ のとき,すなわち,} k=1 \text{ のとき,}&&\text{ 1個}\\ &2k-2<0 \text{ のとき,すなわち,} k<1 \text{ のとき,}&&\text{ 0個}\\ \end{alignedat}$
% 問題I3.3.15
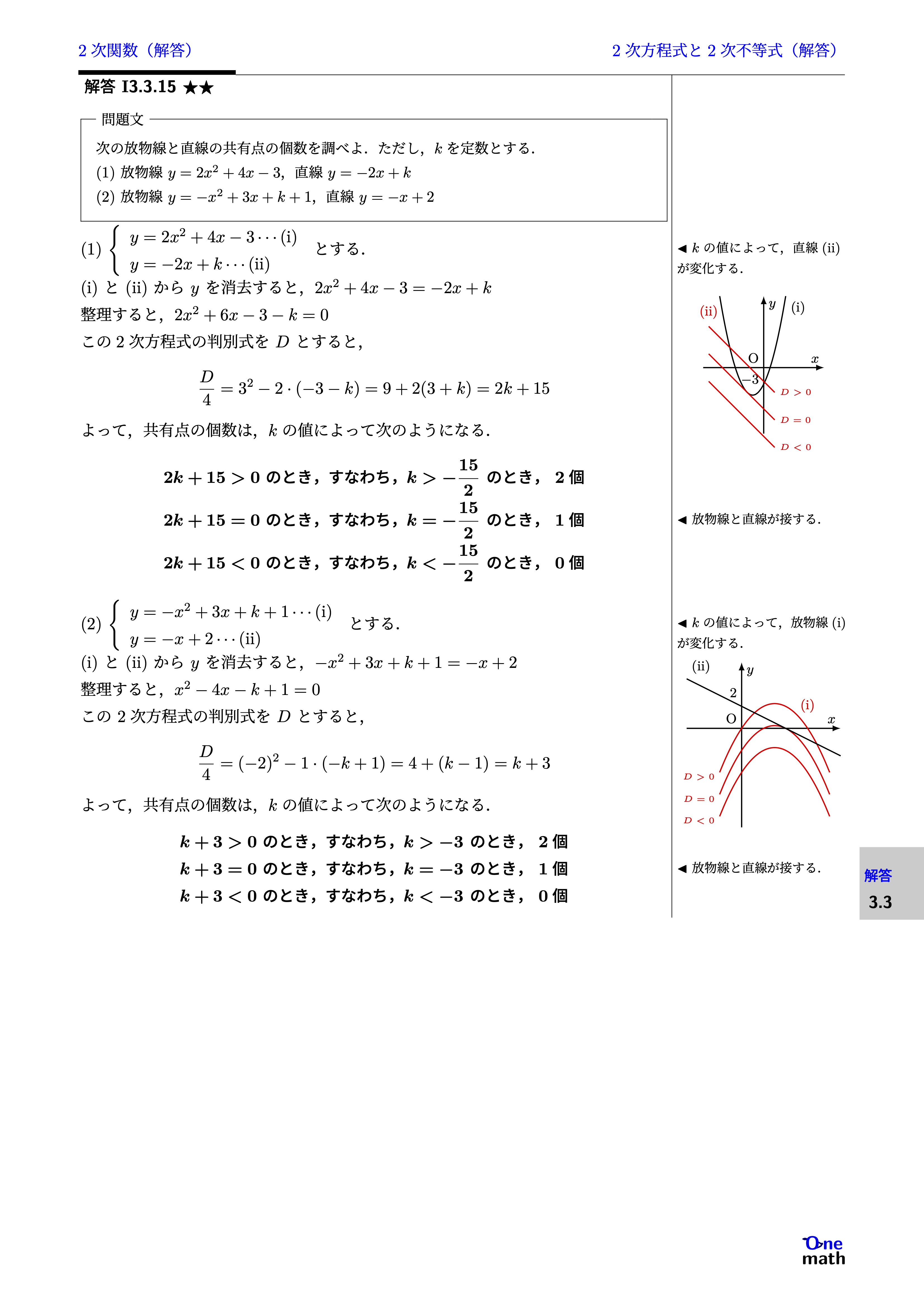
次の放物線と直線の共有点の個数を調べよ.ただし,$k$を定数とする. (1)放物線$y=2x^2+4x-3$,直線$y=-2x+k$(2)放物線$y=-x^2+3x+k+1$,直線$y=-x+2$
% 解答I3.3.15
(1)$\left\{\begin{array}{l}y=2x^2+4x-3 \cdots (\mathrm{i})\\ y=-2x+k \cdots (\mathrm{ii})\end{array}\right.$とする. (i)と(ii)から$y$を消去すると,$2x^2+4x-3=-2x+k$整理すると,$2x^2+6x-3-k=0$この2次方程式の判別式を$D$とすると,$\frac{D}{4}=3^2-2 \cdot (-3-k)=9+2(3+k)=2k+15$よって,共有点の個数は,$k$の値によって次のようになる.$\begin{alignedat}{2} &2k+15>0 \text{ のとき,すなわち,} k>-\frac{15}{2} \text{ のとき,}&&\text{ 2個}\\ &2k+15=0 \text{ のとき,すなわち,} k=-\frac{15}{2} \text{ のとき,}&&\text{ 1個}\\ &2k+15<0 \text{ のとき,すなわち,} k<-\frac{15}{2} \text{ のとき,}&&\text{ 0個}\\ \end{alignedat}$(2)$\left\{\begin{array}{l}y=-x^2+3x+k+1 \cdots (\mathrm{i})\\ y=-x+2 \cdots (\mathrm{ii})\end{array}\right.$とする. (i)と(ii)から$y$を消去すると,$-x^2+3x+k+1=-x+2$整理すると,$x^2-4x-k+1=0$この2次方程式の判別式を$D$とすると,$\frac{D}{4}=(-2)^2-1 \cdot (-k+1)=4+(k-1)=k+3$よって,共有点の個数は,$k$の値によって次のようになる.$\begin{alignedat}{2} &k+3>0 \text{ のとき,すなわち,} k>-3 \text{ のとき,}&&\text{ 2個}\\ &k+3=0 \text{ のとき,すなわち,} k=-3 \text{ のとき,}&&\text{ 1個}\\ &k+3<0 \text{ のとき,すなわち,} k<-3 \text{ のとき,}&&\text{ 0個}\\ \end{alignedat}$