% 例題I3.3.23:ある区間で常に成り立つ不等式 (One More)★★★
$0 \leqq x \leqq 8$のすべての$x$の値に対して,不等式$x^2-2 a x+a+2>0$が成り立つような定数$a$の値の範囲を求めよ.
% 解答(例題I3.3.23)
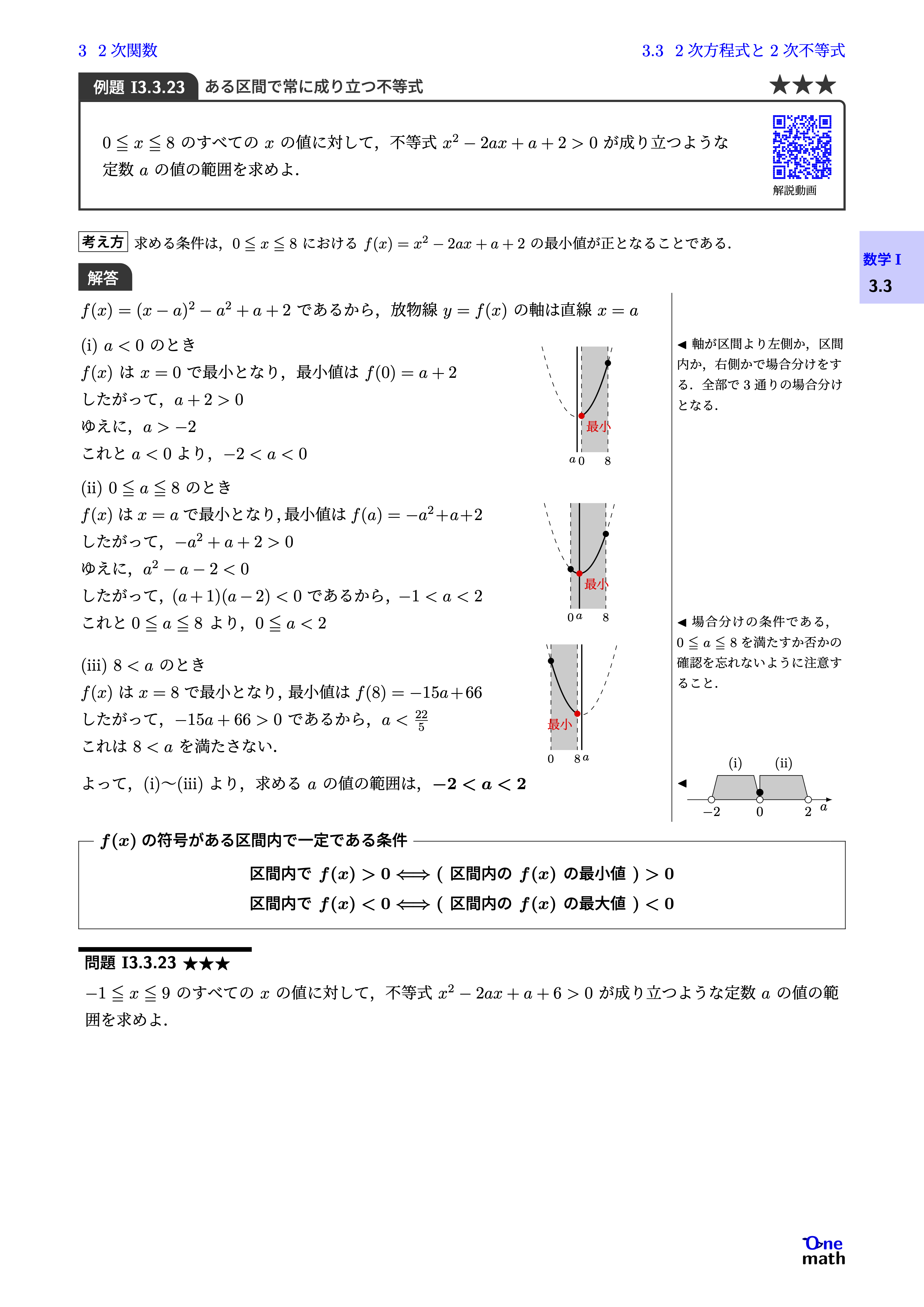
$f(x)=(x-a)^2-a^2+a+2$であるから,放物線$y=f(x)$の軸は直線$x=a$(i)$a<0$のとき$f(x)$は$x=0$で最小となり,最小値は$f(0)=a+2$したがって,$a+2>0$ゆえに,$a>-2$これと$a<0$より,$-2<a<0$(ii)$0 \leqq a \leqq 8$のとき$f(x)$は$x=a$で最小となり,最小値は$f(a)=-a^2+a+2$したがって,$-a^2+a+2>0$ゆえに,$a^2-a-2<0$したがって,$(a+1)(a-2)<0$であるから,$-1<a<2$これと$0 \leqq a \leqq 8$より,$0 \leqq a<2$(iii)$8<a$のとき$f(x)$は$x=8$で最小となり,最小値は$f(8)=-15 a+66$したがって,$-15 a+66>0$であるから,$a<\frac{22}{5}$これは$8<a$を満たさない. よって,(i)〜(iii)より,求める$a$の値の範囲は,$-2<a<2$
% 問題I3.3.23
$-1 \leqq x \leqq 9$のすべての$x$の値に対して,不等式$x^2-2 a x+a+6>0$が成り立つような定数$a$の値の範囲を求めよ.
% 解答I3.3.23
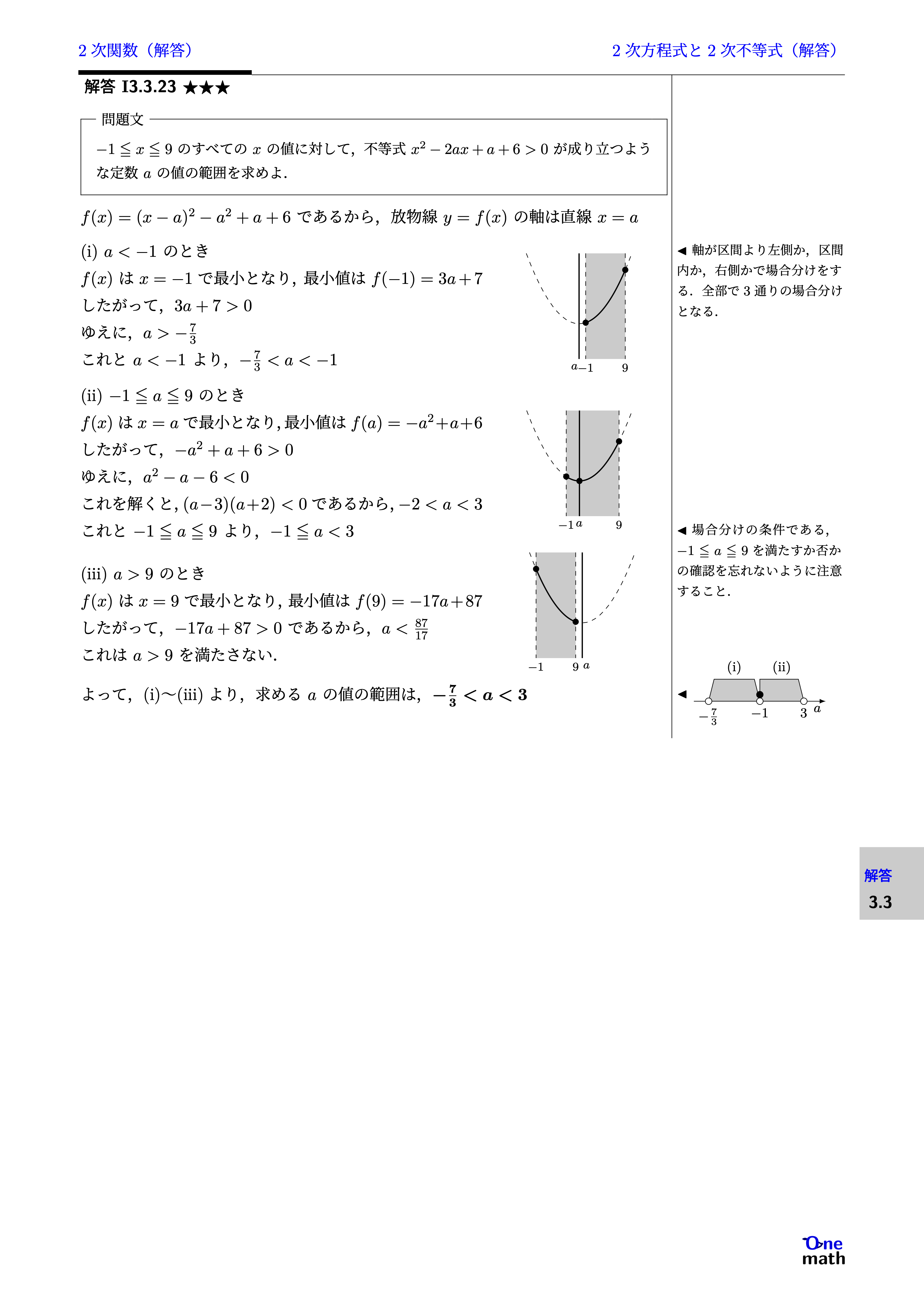
$f(x)=(x-a)^2-a^2+a+6$であるから,放物線$y=f(x)$の軸は直線$x=a$(i)$a<-1$のとき$f(x)$は$x=-1$で最小となり,最小値は$f(-1)=3a+7$したがって,$3a+7>0$ゆえに,$a>-\frac{7}{3}$これと$a<-1$より,$-\frac{7}{3}<a<-1$(ii)$-1 \leqq a \leqq 9$のとき$f(x)$は$x=a$で最小となり,最小値は$f(a)=-a^2+a+6$したがって,$-a^2+a+6>0$ゆえに,$a^2-a-6<0$これを解くと,$(a-3)(a+2)<0$であるから,$-2<a<3$これと$-1 \leqq a \leqq 9$より,$-1 \leqq a<3$(iii)$a>9$のとき$f(x)$は$x=9$で最小となり,最小値は$f(9)=-17a+87$したがって,$-17a+87>0$であるから,$a<\frac{87}{17}$これは$a>9$を満たさない. よって,(i)〜(iii)より,求める$a$の値の範囲は,$-\frac{7}{3}<a<3$