% 例題I3.3.25:方程式の解の存在範囲1 (One More)★★★
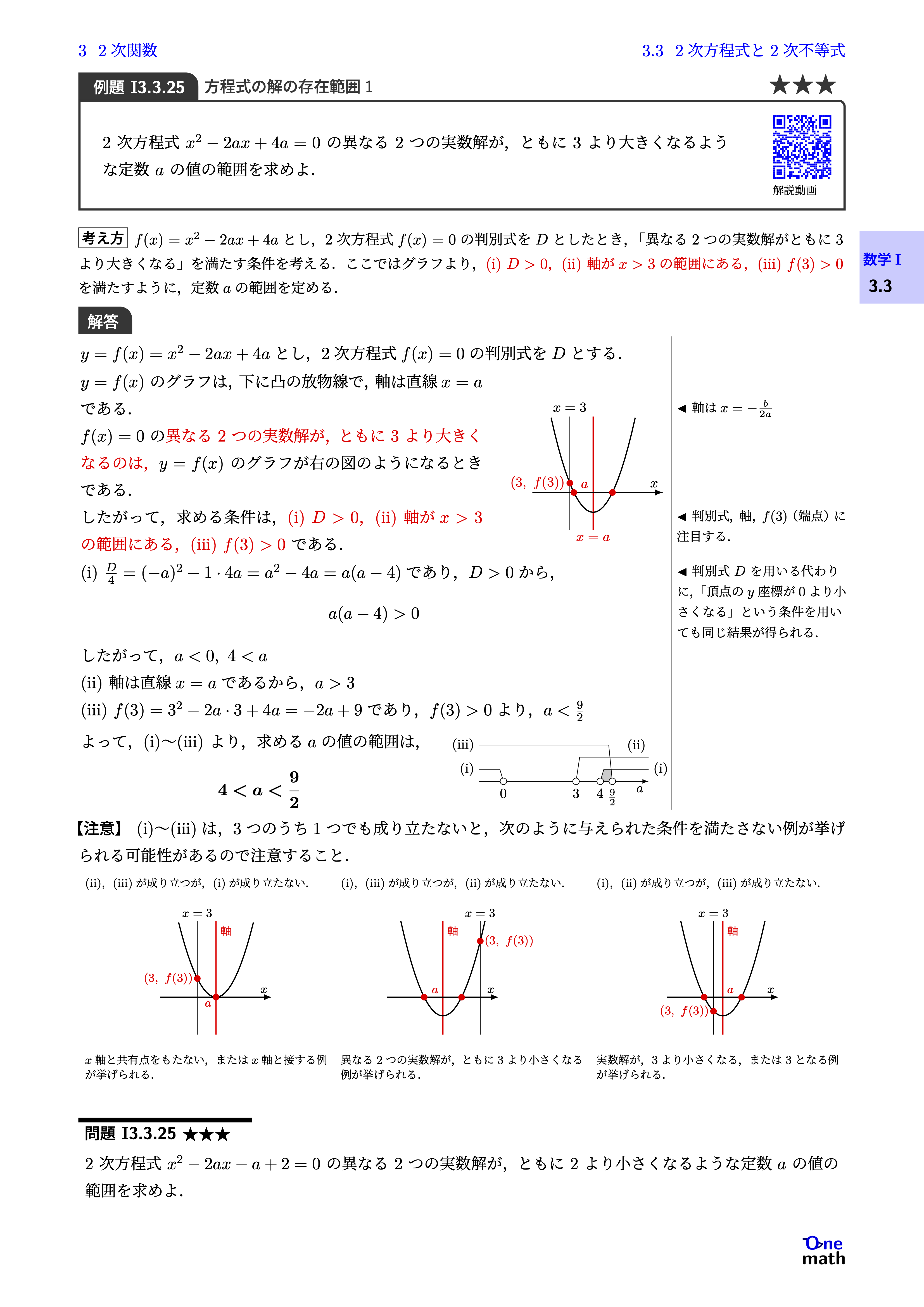
2次方程式$x^2-2a x+4 a=0$の異なる2つの実数解が,ともに3より大きくなるような定数$a$の値の範囲を求めよ.
% 解答(例題I3.3.25)
$y=f(x)=x^2-2ax+4 a$とし,2次方程式$f(x)=0$の判別式を$D$とする.$y=f(x)$のグラフは,下に凸の放物線で,軸は直線$x=a$である.$f(x)=0$の異なる2つの実数解が,ともに3より大きくなるのは,$y=f(x)$のグラフが右の図のようになるときである. したがって,求める条件は, (i)$D>0$, (ii)軸が$x>3$の範囲にある, (iii)$f(3)>0$である. (i)$\frac{D}{4}=(-a)^2-1 \cdot 4a=a^2-4a=a(a-4)$であり,$D>0$から,$a(a-4)>0$したがって,$a<0,4<a$(ii)軸は直線$x=a$であるから,$a>3$(iii)$f(3)=3^2-2a \cdot 3+4a=-2a+9$であり,$f(3)>0$より,$a<\frac{9}{2}$よって,(i)〜(iii)より,求める$a$の値の範囲は,$4<a<\frac{9}{2}$
% 問題I3.3.25
2次方程式$x^2-2a x-a+2=0$の異なる2つの実数解が,ともに$2$より小さくなるような定数$a$の値の範囲を求めよ.
% 解答I3.3.25
$y=f(x)=x^2-2ax-a+2$とし,2次方程式$f(x)=0$の判別式を$D$とする.$y=f(x)$のグラフは,下に凸の放物線で,軸は直線$x=a$である.$f(x)=0$の異なる2つの実数解が,ともに$2$より小さくなるのは,$y=f(x)$のグラフが右の図のようになるときである. したがって,求める条件は, (i)$D>0$, (ii)軸が$x<2$の範囲にある, (iii)$f(2)>0$である. (i)$\frac{D}{4}=(-a)^2-1 \cdot (-a+2)=a^2+a-2=(a+2)(a-1)$であり,$D>0$であるから,$(a+2)(a-1)>0$したがって,$a<-2,1<a$(ii)軸は直線$x=a$であるから,$a<2$(iii)$f(2)=2^2-2a \cdot 2-a+2=-5a+6$であり,$f(2)>0$より,$a<\frac{6}{5}$よって,(i)〜(iii)より,求める$a$の値の範囲は,$a<-2,1<a<\frac{6}{5}$