% 例題I3.3.33:2次不等式の文章題 (One More)★★
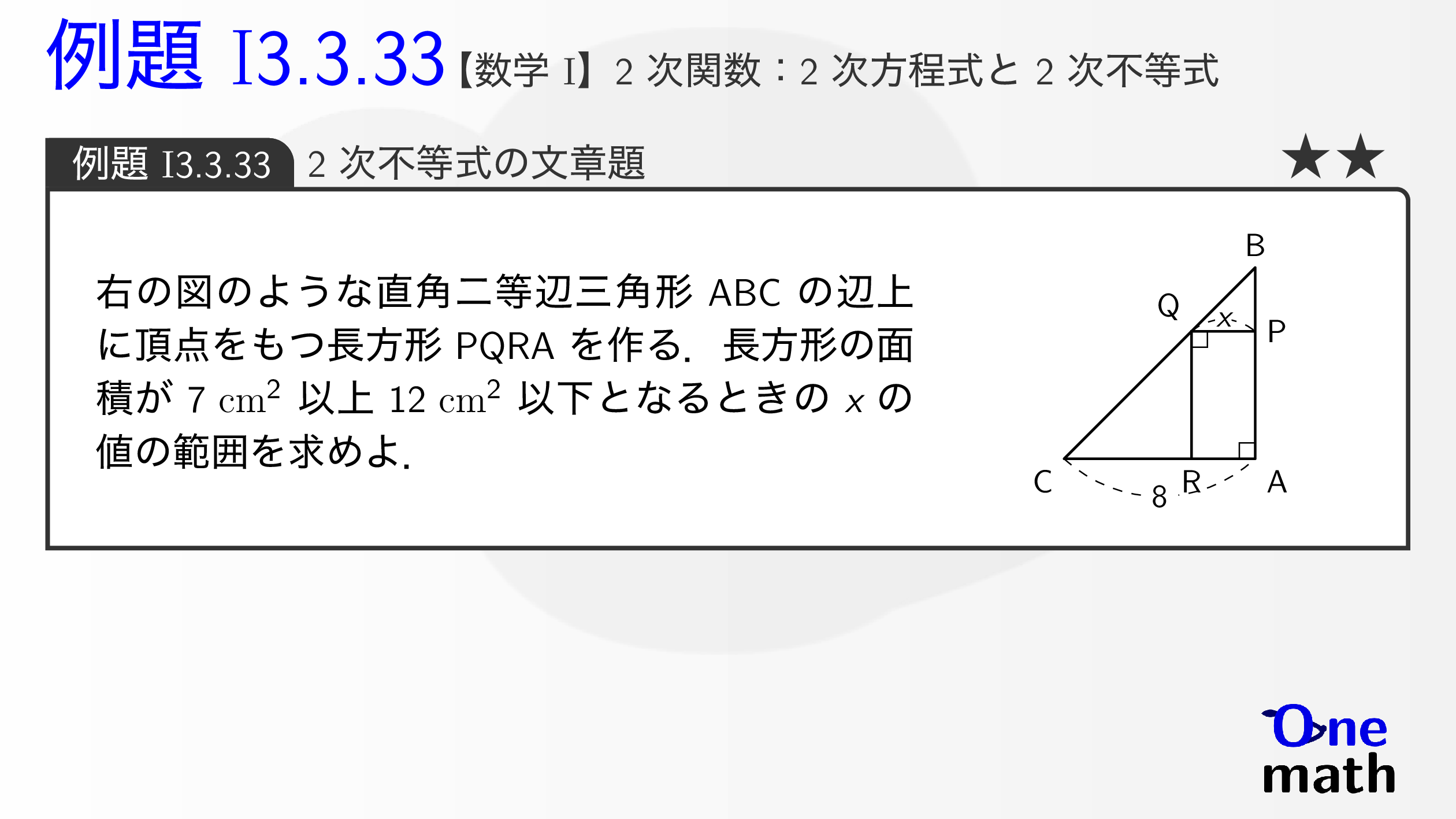
右の図のような直角二等辺三角形ABCの辺上に頂点をもつ長方形PQRAを作る.長方形の面積が$7 \mathrm{cm}^2$以上$12 \mathrm{cm}^2$以下となるときの$x$の値の範囲を求めよ.
% 解答(例題I3.3.33)
$\mathrm{BP}=\mathrm{PQ}=x$であるから,$$\mathrm{PA}=\mathrm{BA}-\mathrm{BP}=8-x$$$x>0,8-x>0$であるから,$0<x<8 \cdots (\mathrm{i})$長方形PQRAの面積は$x(8-x)\mathrm{cm}^2$が$7\mathrm{cm}^2$以上$12\mathrm{cm}^2$であるから,$$7 \leqq x(8-x) \leqq 12$$$7 \leqq x(8-x)$より,$x^2-8 x+7 \leqq 0$したがって,$(x-1)(x-7) \leqq 0$ゆえに,$1 \leqq x \leqq 7 \cdots (\mathrm{ii})$$x(8-x) \leqq 12$より,$x^2-8 x+12 \geqq 0$したがって,$(x-2)(x-6) \geqq 0$ゆえに,$x \leqq 2,6 \leqq x \cdots (\mathrm{iii})$よって,(i)〜(iii)の共通範囲を求めると,$$1 \leqq x \leqq 2,6 \leqq x \leqq 7$$
% 問題I3.3.33
長さ40cmの針金を2つに分け,それぞれを折り曲げて正方形を2つ作る.2つの正方形の面積の和が$52 \mathrm{cm}^2$以上になるようにするには,針金をどのように切ればよいか.短い方の針金の長さの範囲を求めよ.
% 解答I3.3.33
短い方の針金の長さを$4 x \mathrm{cm}$とすると,長い方の針金の長さは,$$40-4 x=4(10-x)(\mathrm{cm})$$$0<4 x<20$より,$0<x<5 \cdots (\mathrm{i})$2つの正方形の1辺の長さは,それぞれ$x \mathrm{cm}$と$10-x \mathrm{cm}$であるから,$$x^2+(10-x)^2 \geqq 52$$整理すると,$x^2-10 x+24 \geqq 0$したがって,$(x-6)(x-4) \geqq 0$ゆえに,$x \leqq 4,6 \leqq x \cdots (\mathrm{ii})$(i),(ii)より,$0<x \leqq 4$よって,$0<4 x \leqq 16$となり,短い方の針金の長さは,$0 \mathrm{cm}$より長く,$16 \mathrm{cm}$以下であればよい.