% 例題I3.3.34:2つの放物線の大小関係1 (One More)★★★★
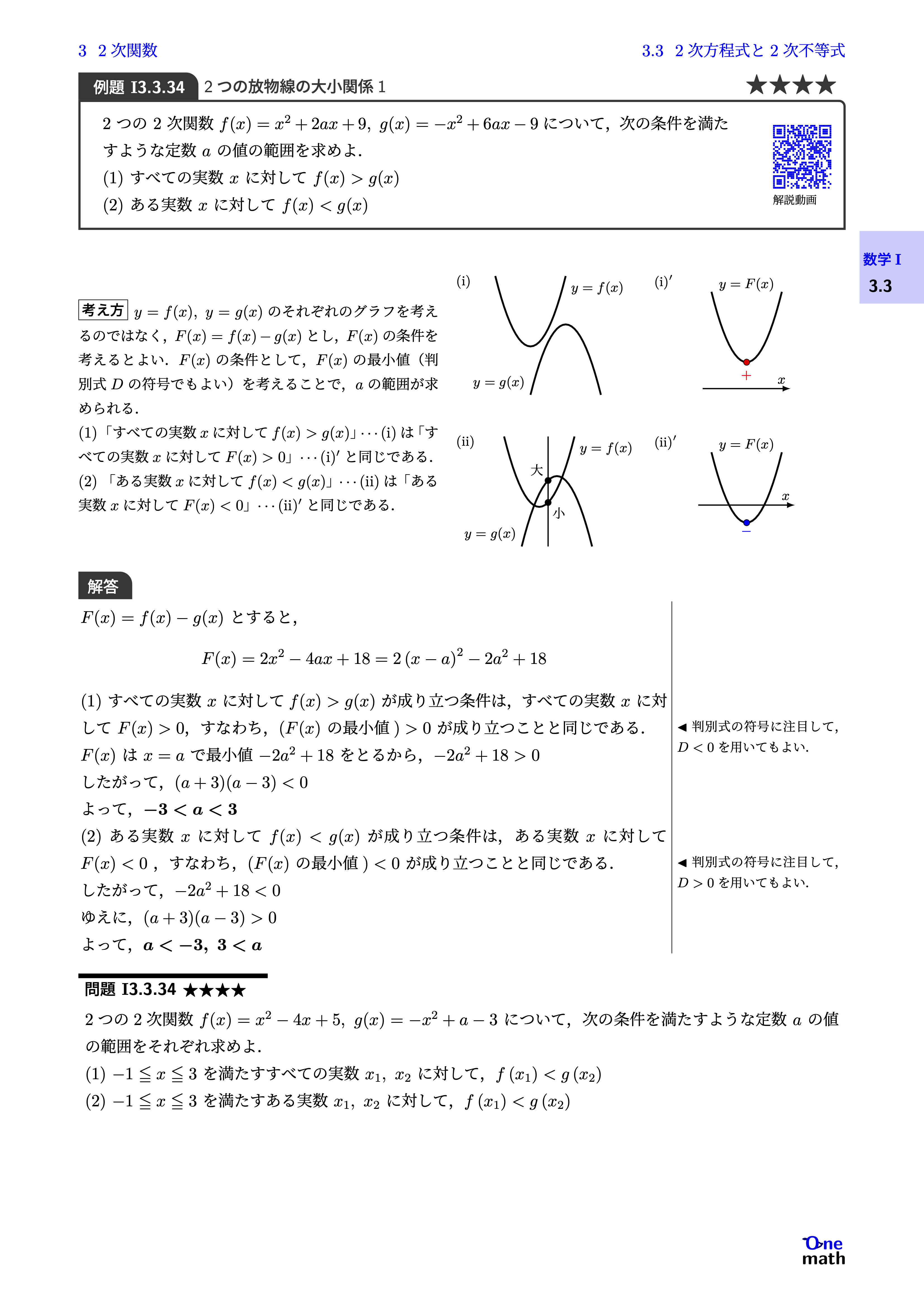
2つの2次関数$f(x)=x^2+2 a x+9,g(x)=-x^2+6ax-9$について,次の条件を満たすような定数$a$の値の範囲を求めよ. (1)すべての実数$x$に対して$f(x)>g(x)$(2)ある実数$x$に対して$f(x)<g(x)$
% 解答(例題I3.3.34)
$F(x)=f(x)-g(x)$とすると,$F(x)=2 x^2-4a x+18=2\left(x-a\right)^2-2a^2+18$(1)すべての実数$x$に対して$f(x)>g(x)$が成り立つ条件は,すべての実数$x$に対して$F(x)>0$,すなわち,$(F(x)$の最小値$)>0$が成り立つことと同じである.$F(x)$は$x=a$で最小値$-2a^2+18$をとるから,$-2a^2+18>0$したがって,$(a+3)(a-3)<0$よって,$-3<a<3$(2)ある実数$x$に対して$f(x)<g(x)$が成り立つ条件は,ある実数$x$に対して$F(x)<0$,すなわち,$(F(x)$の最小値$)<0$が成り立つことと同じである. したがって,$-2a^2+18<0$ゆえに,$(a+3)(a-3)>0$よって,$a<-3,3<a$
% 問題I3.3.34
2つの2次関数$f(x)=x^2-4 x+5,g(x)=-x^2+a-3$について,次の条件を満たすような定数$a$の値の範囲をそれぞれ求めよ. (1)$-1 \leqq x \leqq 3$を満たすすべての実数$x_1,x_2$に対して,$f\left(x_1\right)<g\left(x_2\right)$(2)$-1 \leqq x \leqq 3$を満たすある実数$x_1,x_2$に対して,$f\left(x_1\right)<g\left(x_2\right)$
% 解答I3.3.34
$F(x)=f(x)-g(x)$とすると,$F(x)=2 x^2-4a x+35=2(x-a)^2-2a^2+35$(1)すべての実数$x$に対して$f(x)>g(x)$が成り立つ条件は,すべての実数$x$に対して$F(x)>0$,すなわち,$(F(x)$の最小値$)>0$が成り立つことと同じである.$F(x)$は$x=a$で最小値$-2a^2+35$をとるから,$-2a^2+35>0$したがって,$a^2<\frac{35}{2}$よって,$-\frac{\sqrt{70}}{2}<a<\frac{\sqrt{70}}{2}$(2)ある実数$x$に対して$f(x)<g(x)$が成り立つ条件は,ある実数$x$に対して$F(x)<0$,すなわち,$(F(x)$の最小値$)<0$が成り立つことと同じである. したがって,$-2a^2+35<0$ゆえに,$a^2>\frac{35}{2}$よって,$a<-\frac{\sqrt{70}}{2},\frac{\sqrt{70}}{2}<a$