% 例題I4.1.11:三角比を含む不等式1 (One More)★★
次の不等式を満たす$\theta$の値の範囲を求めよ.ただし,$0^{\circ} \leqq \theta \leqq 180^{\circ}$とする. (1)$\sin \theta \geqq\frac{1}{2}$(2)$\cos \theta<-\frac{1}{2}$
% 解答(例題I4.1.11)
(1)$\sin \theta =\frac{1}{2}$より,$\theta=30^{\circ},150^{\circ}$よって,右の図より,$\sin \theta \geqq\frac{1}{2}$となる$\theta$の値の範囲は,$30^{\circ} \leqq \theta \leqq 150^{\circ}$(2)$\cos \theta=-\frac{1}{2}$より,$\theta=120^{\circ}$よって,右の図より,$\cos \theta<-\frac{1}{2}$となる$\theta$の 値の範囲は,$120^{\circ}<\theta \leqq 180^{\circ}$
% 問題I4.1.11
次の不等式を満たす$\theta$の値の範囲を求めよ.ただし,$0^{\circ} \leqq \theta \leqq 180^{\circ}$とする. (1)$\sin \theta>\frac{\sqrt{3}}{2}$(2)$\cos \theta \leqq -\frac{\sqrt{2}}{2}$
% 解答I4.1.11
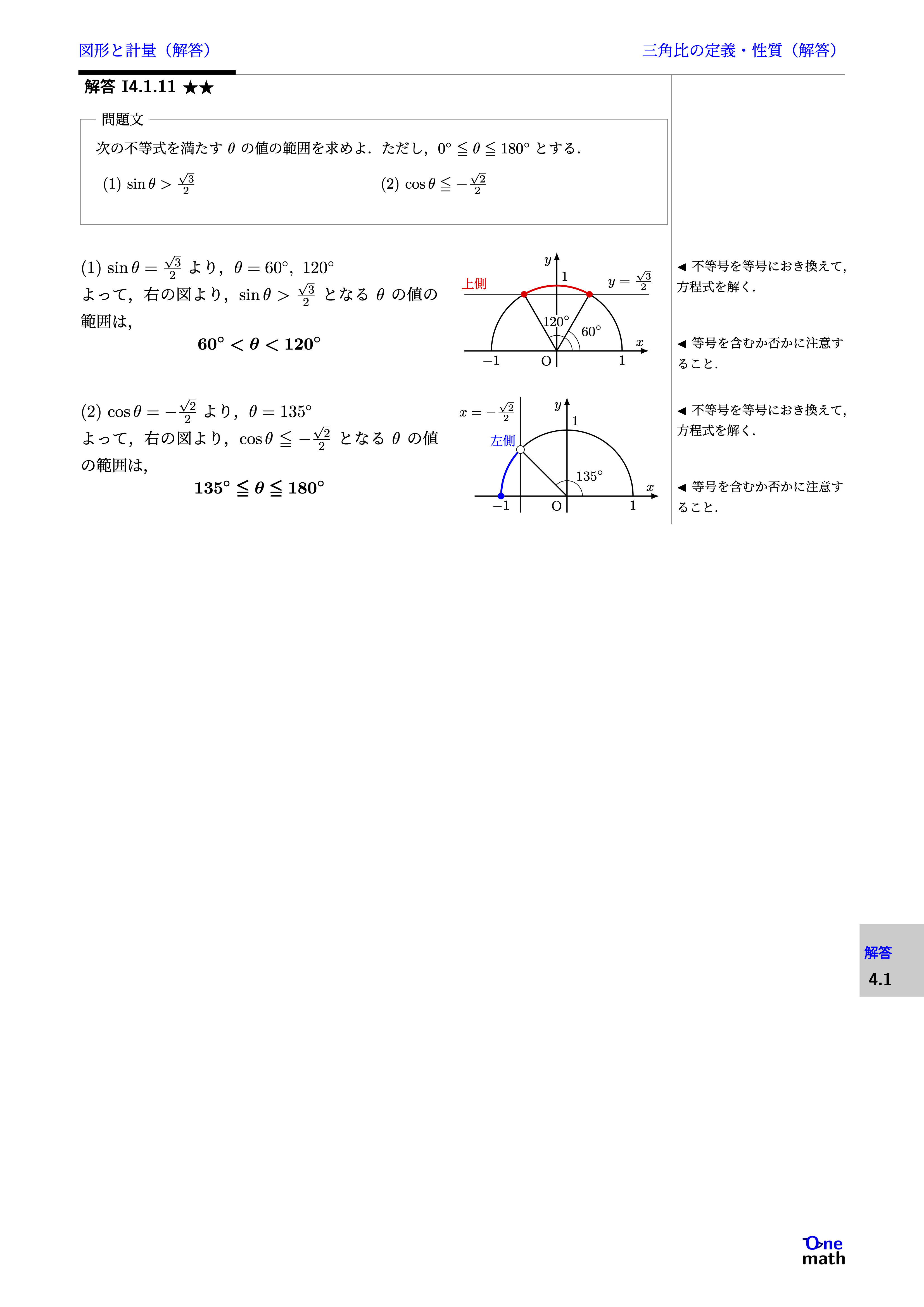
(1)$\sin \theta=\frac{\sqrt{3}}{2}$より,$\theta=60^{\circ},120^{\circ}$よって,右の図より,$\sin \theta>\frac{\sqrt{3}}{2}$となる$\theta$の値の範囲は,$60^{\circ}<\theta<120^{\circ}$(2)$\cos \theta=-\frac{\sqrt{2}}{2}$より,$\theta=135^{\circ}$よって,右の図より,$\cos \theta \leqq -\frac{\sqrt{2}}{2}$となる$\theta$の 値の範囲は,$135^{\circ} \leqq \theta \leqq 180^{\circ}$