% 例題I4.3.11:空間図形における最短距離 (One More)★★★
底面の中心がOで半径が3,高さが$6\sqrt{2}$の直円錐がある.直円錐の頂点をA,底面の直径の両端をB,Cとし,線分AC上に$\mathrm{AP}=3$となる点Pをとる.側面上において,点Bから点Pまでに至る最短距離を求めよ.
% 解答(例題I4.3.11)
側面を直線ABに沿って切り開いた展開図は,右の図のように,中心A,半径ABの扇形となる. 三角形ABOにおいて,$\mathrm{BO}=3,\mathrm{AO}=6\sqrt{2}$より,$$\mathrm{AB=\sqrt{3^2+(6\sqrt{2})^2}=9}$$求める最短距離の長さは,展開図において,線分BPの長さである. 弧$\mathrm{BCB}^{\prime}$の長さは,$2 \pi \cdot 3=6 \pi$扇形の半径は9であるから,中心角$\angle \mathrm{BAB}^\prime$は,$$\angle \mathrm{BAB}^{\prime}=360^{\circ} \times\frac{6 \pi}{2 \pi \cdot 9}=120^{\circ}$$したがって,$\angle \mathrm{BAC}=60^{\circ}$$\triangle \mathrm{ABP}$において,余弦定理より,$$\mathrm{BP}^2 =9^2+3^2-2 \cdot 9 \cdot 3 \cdot \cos 60^{\circ} =90-54 \cdot \frac{1}{2}=63$$よって,$\mathrm{BP}>0$より,$\mathrm{BP}=3\sqrt{7}$
% 問題I4.3.11
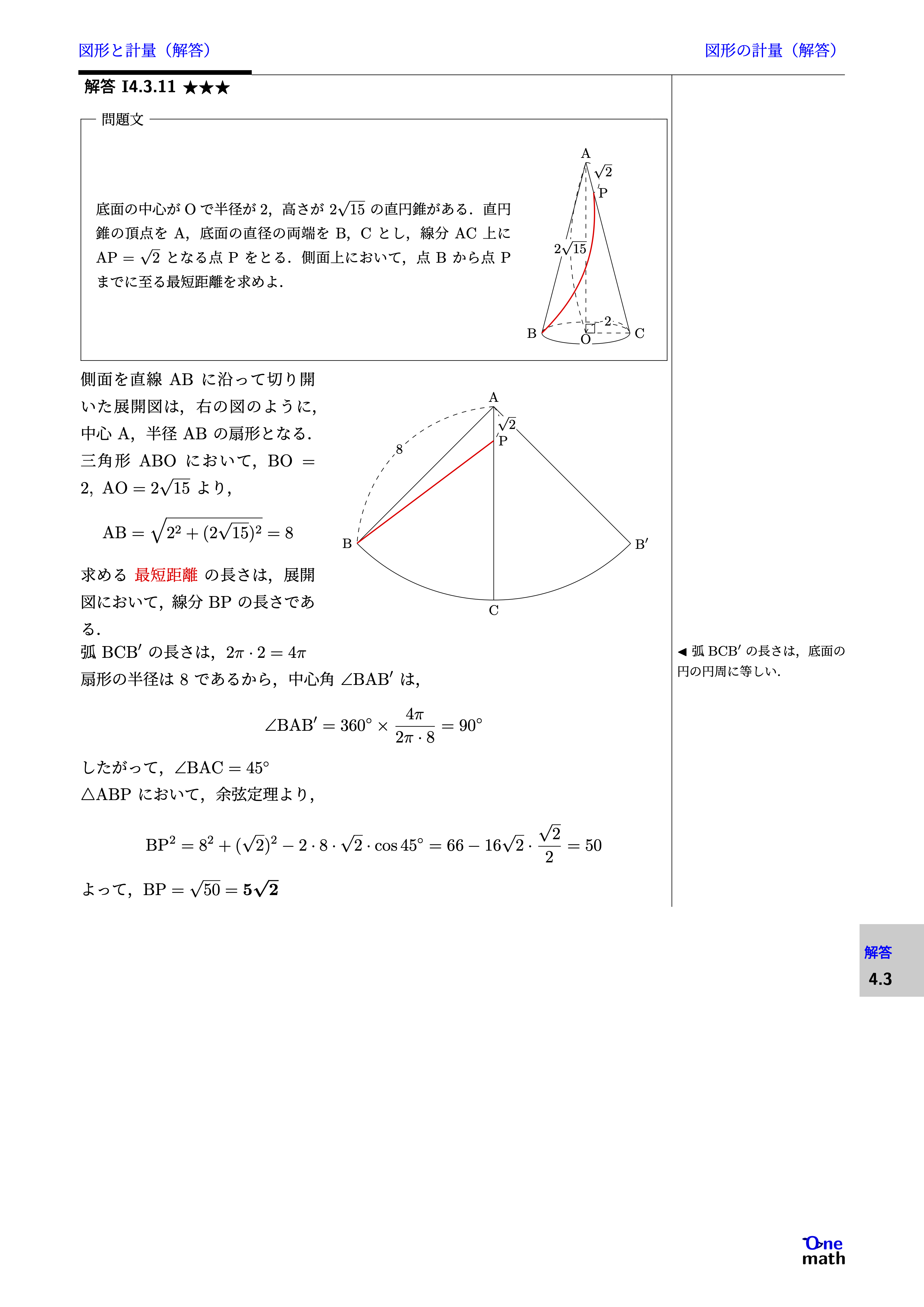
底面の中心がOで半径が2,高さが$2\sqrt{15}$の直円錐がある.直円錐の頂点をA,底面の直径の両端をB,Cとし,線分AC上に$\mathrm{AP}=\sqrt{2}$となる点Pをとる.側面上において,点Bから点Pまでに至る最短距離を求めよ.
% 解答I4.3.11
側面を直線ABに沿って切り開いた展開図は,右の図のように,中心A,半径ABの扇形となる. {三角形ABO}において,$\mathrm{BO}=2,\mathrm{AO}=2\sqrt{15}$より,$${\mathrm{AB}=\sqrt{2^2+(2\sqrt{15})^2}=8}$$求める最短距離の長さは,展開図において,線分BPの長さである. 弧$\mathrm{BCB}^{\prime}$の長さは,$2 \pi \cdot 2=4 \pi$扇形の半径は$8$であるから,中心角$\angle \mathrm{BAB}^\prime$は,$$\angle \mathrm{BAB}^{\prime}=360^{\circ} \times\frac{4 \pi}{2 \pi \cdot 8}=90^{\circ}$$したがって,$\angle \mathrm{BAC}=45^{\circ}$$\triangle \mathrm{ABP}$において,余弦定理より,$$\mathrm{BP}^2 =8^2+(\sqrt{2})^2-2 \cdot 8 \cdot \sqrt{2} \cdot \cos 45^{\circ} =66-16\sqrt{2} \cdot \frac{\sqrt{2}}{2}=50$$よって,$\mathrm{BP}=\sqrt{50}=5\sqrt{2}$