% 基本事項A3.1.1:角(One More)
(1)対頂角の性質 対頂角が等しい.$\left(\alpha=\alpha^{\prime}\right)$ (2)平行線と同位角・錯角の性質 $$ \begin{aligned} &\text{2直線} l,m \text{ に直線 } n \text{が交わるとき,} \\ &l \parallel m \Longleftrightarrow \text{同位角が等しい}(\alpha = \beta) . \\ &l \parallel m \Longleftrightarrow \text{錯角が等しい}(\alpha = \gamma). \\ &l \parallel m \Longleftrightarrow \text{同じ側の内角の和が } 180^{\circ} \text{になる.}(\alpha+\delta = 180^\circ) \end{aligned} $$ (3)多角形の内角・外角の和 $$ \begin{aligned} &\text{三角形の内角の和は,} 180^\circ \text{である.} \\ &\text{三角形の外角はその隣にない2つの内角の和に等しい.} \\ &n \text{角形の内角の和は,} 180^\circ \times (n-2) \text{である.} \\ &\text{多角形の外角の和は,} 360^\circ \text{である.} \end{aligned} $$
% 基本事項A3.1.2:二等辺三角形の性質(One More)
$\triangle \mathrm{ABC}$において,$\mathrm{AB}=\mathrm{AC}\Longleftrightarrow\angle \mathrm{B}=\angle \mathrm{C}$ 二等辺三角形の頂角の二等分線は,底辺を垂直に2等分する. 2つの角が等しい三角形は,二等辺三角形である.
% 基本事項A3.1.3:三角形の合同条件(One More)
(i)3辺がそれぞれ等しい. (ii)2辺とその間の角がそれぞれ等しい. (iii)1辺とその両端の角がそれぞれ等しい. とくに,直角三角形の合同条件は次のようになる. (i)斜辺と1つの鋭角がそれぞれ等しい. (ii)斜辺と他の1辺がそれぞれ等しい.
% 基本事項A3.1.4:三角形の相似条件(One More)
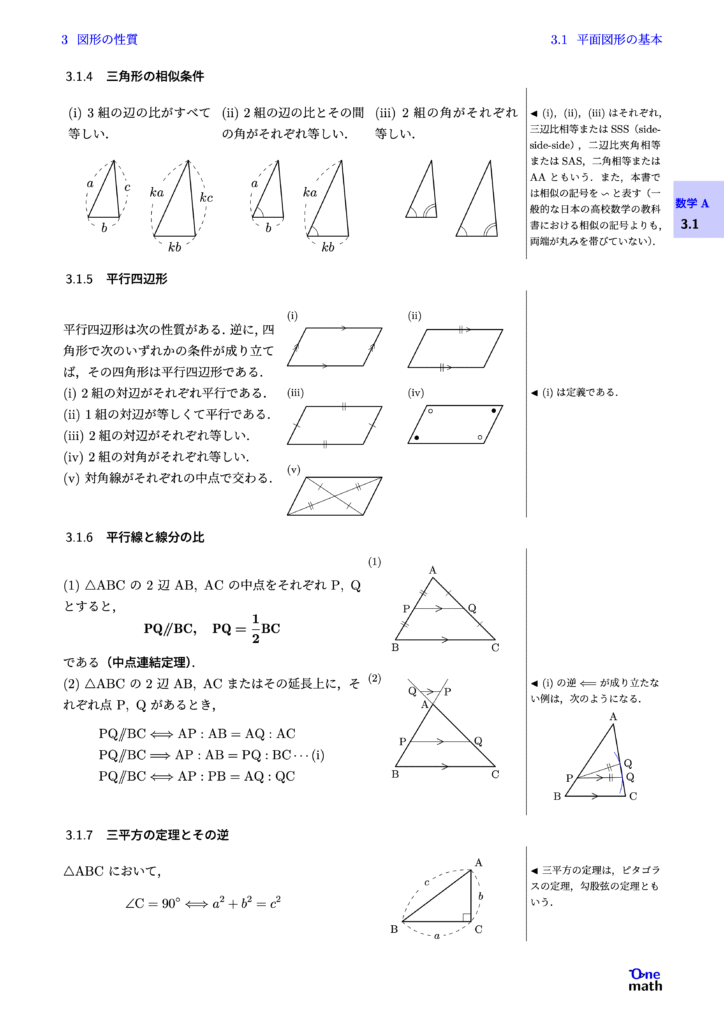
(i)3組の辺の比がすべて等しい. (ii)2組の辺の比とその間の角がそれぞれ等しい. (iii)2組の角がそれぞれ等しい.
% 基本事項A3.1.5:平行四辺形(One More)
平行四辺形は次の性質がある.逆に,四角形で次のいずれかの条件が成り立てば,その四角形は平行四辺形である. (i)2組の対辺がそれぞれ平行である. (ii)1組の対辺が等しくて平行である. (iii)2組の対辺がそれぞれ等しい. (iv)2組の対角がそれぞれ等しい. (v)対角線がそれぞれの中点で交わる.
% 基本事項A3.1.6:平行線と線分の比(One More)
(1)$\triangle \mathrm{ABC}$の2辺$\mathrm{AB},\mathrm{AC}$の中点をそれぞれ$\mathrm{P},\mathrm{Q}$とすると, $$\mathrm{PQ} \parallel \mathrm{BC},\mathrm{PQ}=\frac{1}{2} \mathrm{BC}$$ である(中点連結定理). (2)$\triangle \mathrm{ABC}$の2辺$\mathrm{AB},\mathrm{AC}$またはその延長上に,それぞれ点$\mathrm{P},\mathrm{Q}$があるとき, $$ \begin{aligned} \mathrm{PQ} \parallel \mathrm{BC} &\Longleftrightarrow \mathrm{AP}: \mathrm{AB}=\mathrm{AQ}: \mathrm{AC} \\ \mathrm{PQ} \parallel \mathrm{BC} &\Longrightarrow \mathrm{AP}: \mathrm{AB}=\mathrm{PQ}: \mathrm{BC} \cdots (\mathrm{i})\\ \mathrm{PQ} \parallel \mathrm{BC} &\Longleftrightarrow \mathrm{AP}: \mathrm{PB}=\mathrm{AQ}: \mathrm{QC} \end{aligned} $$
% 基本事項A3.1.7:三平方の定理とその逆(One More)
$\triangle \mathrm{ABC}$において,$$\angle \mathrm{C}=90^{\circ} \Longleftrightarrow a^2+b^2=c^2$$
% 基本事項A3.1.8:内分点と外分点(One More)
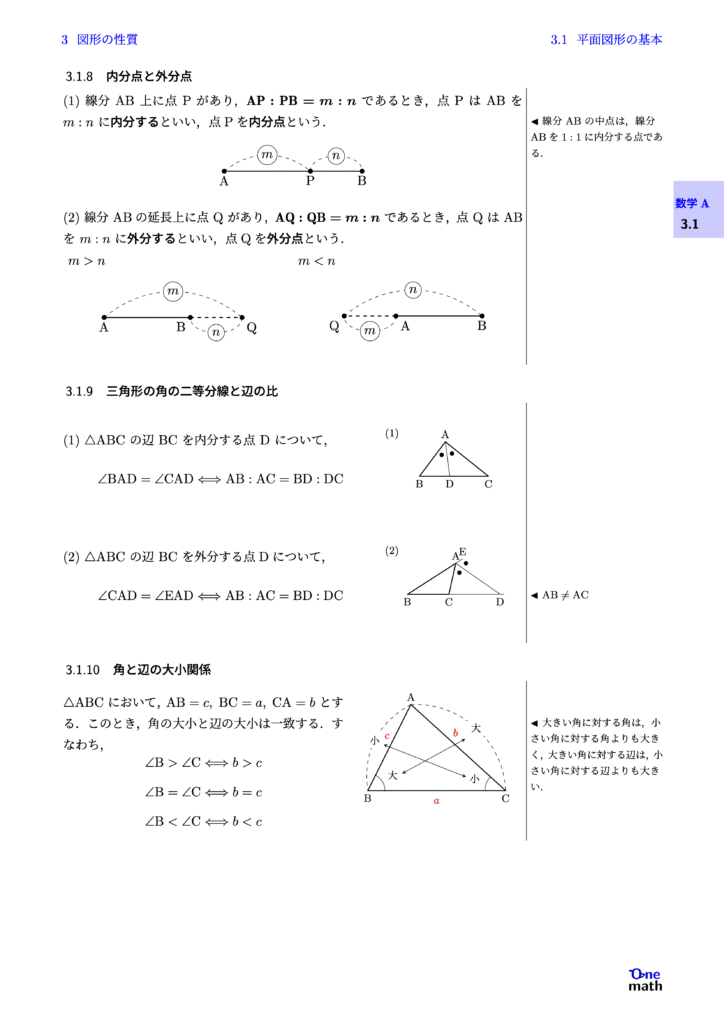
(1)線分$\mathrm{AB}$上に点$\mathrm{P}$があり,$\mathrm{AP}: \mathrm{PB}=m: n$であるとき,点$\mathrm{P}$は$\mathrm{AB}$を$m: n$に内分するといい,点Pを内分点という. (2)線分$\mathrm{AB}$の延長上に点$\mathrm{Q}$があり,$\mathrm{A Q}: \mathrm{Q B}=m: n$であるとき,点$\mathrm{Q}$は$\mathrm{AB}$を$m: n$に外分するといい,点Qを\textbf{外分点}という.
% 基本事項A3.1.9:三角形の角の二等分線と辺の比(One More)
(1)$\triangle \mathrm{ABC}$の辺$\mathrm{BC}$を内分する点$\mathrm{D}$について, $$\angle \mathrm{BAD}=\angle \mathrm{CAD}\Longleftrightarrow \mathrm{AB}: \mathrm{AC}=\mathrm{BD}: \mathrm{DC}$$ (2)$\triangle \mathrm{ABC}$の辺$\mathrm{BC}$を外分する点Dについて, $$\angle \mathrm{CAD}=\angle \mathrm{EAD}\Longleftrightarrow \mathrm{AB}: \mathrm{AC}=\mathrm{BD}: \mathrm{DC}$$
% 基本事項A3.1.10:角と辺の大小関係(One More)
$\triangle \mathrm{ABC}$において,$\mathrm{AB}=c,\mathrm{BC}=a,\mathrm{CA}=b$とする.このとき,角の大小と辺の大小は一致する.すなわち, $$ \angle\mathrm{B}>\angle\mathrm{C} \Longleftrightarrow b>c $$ $$ \angle\mathrm{B}=\angle\mathrm{C} \Longleftrightarrow b=c $$ $$ \angle\mathrm{B}<\angle\mathrm{C} \Longleftrightarrow b<c $$
% 基本事項A3.1.11:三角形の五心(One More)
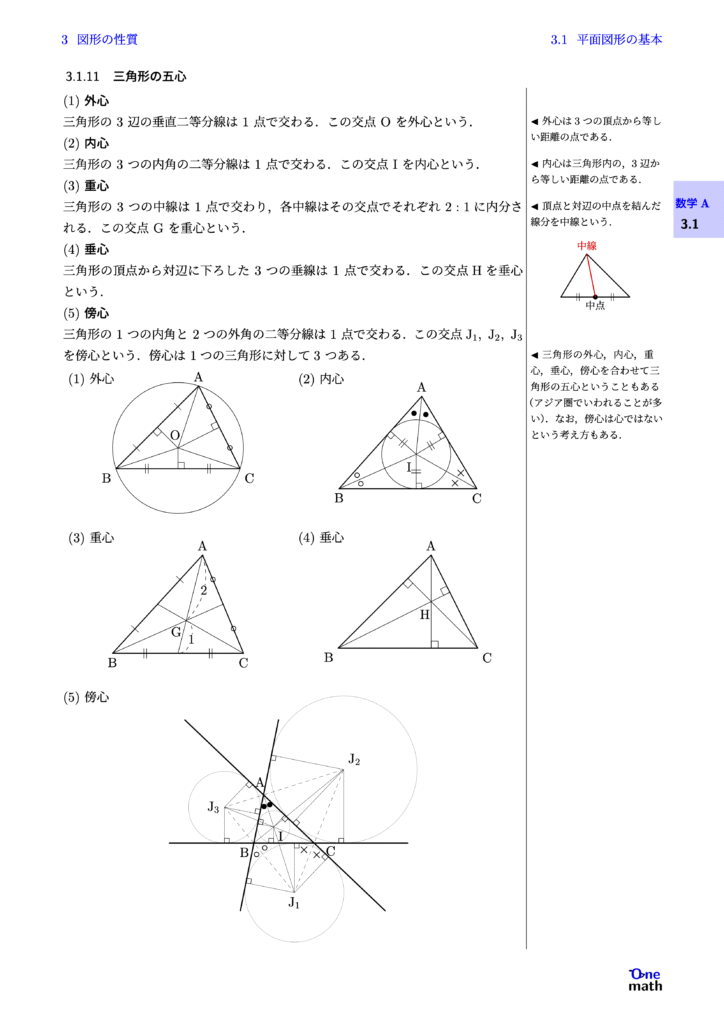
(1)外心 三角形の3辺の垂直二等分線は1点で交わる.この交点$\mathrm{O}$を外心という. (2)内心 三角形の3つの内角の二等分線は1点で交わる.この交点$\mathrm{I}$を内心という. (3)重心 三角形の3つの中線は1点で交わり,各中線はその交点でそれぞれ$2:1$に内分される.この交点Gを重心という. (4)垂心 三角形の頂点から対辺に下ろした3つの垂線は1点で交わる.この交点Hを垂心という. (5)傍心 三角形の1つの内角と2つの外角の二等分線は1点で交わる.この交点$\mathrm{J}_1,\mathrm{J}_2,\mathrm{J}_3$を傍心という.傍心は1つの三角形に対して3つある.
% 基本事項A3.1.12:チェバの定理とメネラウスの定理(One More)
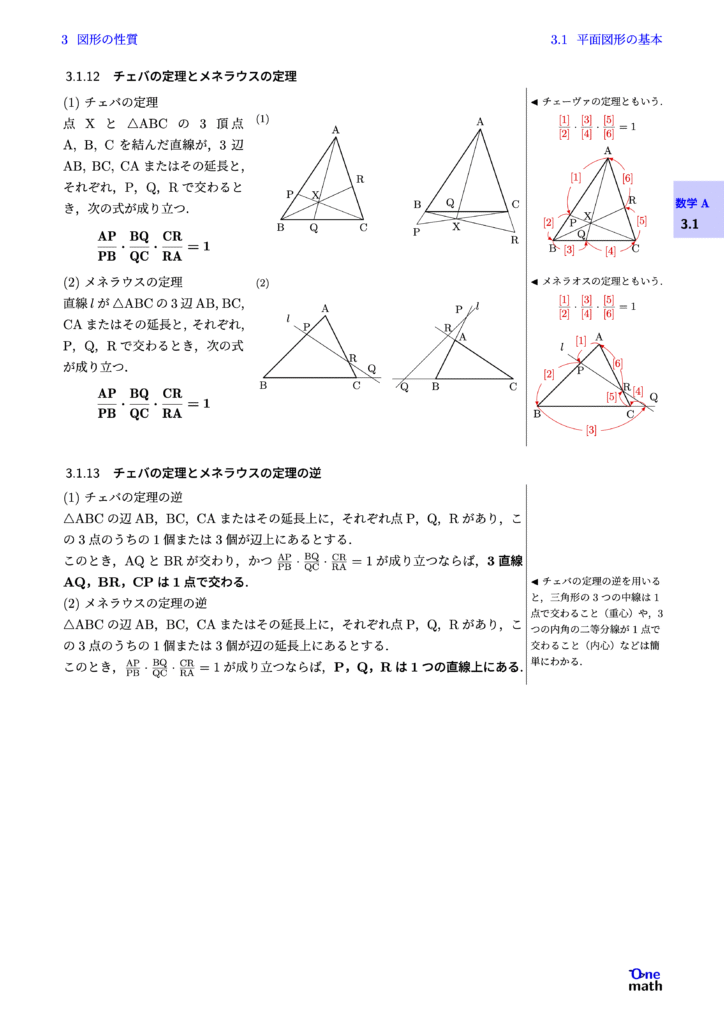
(1)チェバの定理 点Xと$\triangle \mathrm{ABC}$の3頂点$\mathrm{A},\mathrm{B},\mathrm{C}$を結んだ直線が,3辺$\mathrm{AB},\mathrm{BC},\mathrm{CA}$またはその延長と,それぞれ,P,Q,Rで交わるとき,次の式が成り立つ. $$ \frac{\mathrm{AP}}{\mathrm{PB}} \cdot \frac{\mathrm{BQ}}{\mathrm{QC}} \cdot \frac{\mathrm{CR}}{\mathrm{RA}}=1 $$ (2)メネラウスの定理 直線$l$が$\triangle\mathrm{ABC}$の3辺AB,BC,CAまたはその延長と,それぞれ,P,Q,Rで交わるとき,次の式が成り立つ. $$ \frac{\mathrm{AP}}{\mathrm{PB}} \cdot \frac{\mathrm{BQ}}{\mathrm{QC}} \cdot \frac{\mathrm{CR}}{\mathrm{RA}}=1 $$
% 基本事項A3.1.13:チェバの定理とメネラウスの定理の逆(One More)
(1)チェバの定理の逆 $\triangle\mathrm{ABC}$の辺AB,BC,CAまたはその延長上に,それぞれ点P,Q,Rがあり,この3点のうちの1個または3個が辺上にあるとする. このとき,AQとBRが交わり,かつ$\frac{\mathrm{AP}}{\mathrm{PB}} \cdot \frac{\mathrm{BQ}}{\mathrm{QC}} \cdot \frac{\mathrm{CR}}{\mathrm{RA}}=1$が成り立つならば,3直線AQ,BR,CPは1点で交わる. (2)メネラウスの定理の逆 $\triangle\mathrm{ABC}$の辺AB,BC,CAまたはその延長上に,それぞれ点P,Q,Rがあり,この3点のうちの1個または3個が辺の延長上にあるとする. このとき,$\frac{\mathrm{AP}}{\mathrm{PB}} \cdot \frac{\mathrm{BQ}}{\mathrm{QC}} \cdot \frac{\mathrm{CR}}{\mathrm{RA}}=1$が成り立つならば,P,Q,Rは1つの直線上にある.
% 基本事項A3.2.1:円周角の定理とその逆(One More)
(1)円周角の定理 同じ弧に対する円周角の大きさは等しい.円周角の大きさは,その弧に対する中心角の大きさの半分である. $$ \angle \mathrm{APB}=\angle \mathrm{AQB}=\frac{1}{2} \angle \mathrm{AOB} $$ (2)3点$\mathrm{A},\mathrm{B},\mathrm{Q}$を通る円において,点$\mathrm{P}$が直線$\mathrm{AB}$について点Qと同じ側にあるとき,次のことが成り立つ. (i)点$\mathrm{P}$が円の内部にある$\Longrightarrow \angle \mathrm{APB}>\angle \mathrm{AQB}$ (ii)点$\mathrm{P}$が周上にある$\Longrightarrow \angle \mathrm{APB}=\angle \mathrm{AQB}$ (iii)点$\mathrm{P}$が円の外部にある$\Longrightarrow \angle \mathrm{APB}<\angle \mathrm{AQB}$ (3)円周角の定理の逆 4点A,B,P,Qにおいて,2点$\mathrm{P},\mathrm{Q}$が直線$\mathrm{AB}$について同じ側にあるとき, $$ \angle \mathrm{APB}=\angle \mathrm{AQB} \Longrightarrow 4 \text { 点 } \mathrm{A},\mathrm{B},\mathrm{P},\mathrm{Q} \text{は同一円周上にある .} $$
% 基本事項A3.2.2:円に内接する四角形(One More)
円に内接する四角形 (1)向かい合う内角の和は$180^{\circ}$である. $$\text{四角形ABCDが円に内接する} \Longleftrightarrow \angle \mathrm{BAD}+\angle \mathrm{BCD}=180^{\circ}$$ (2)1つの内角は,それに向かい合う内角の隣にある外角に等しい. $$\text{四角形ABCDが円に内接する} \Longleftrightarrow \angle \mathrm{BAD}=\angle \mathrm{DCE}$$
% 基本事項A3.2.3:接線の長さ(One More)
円Oの外部の点Aから,その円Oに引いた2本の接線について,2つの接線の長さは等しい. $$ \mathrm{AP}=\mathrm{AQ} $$
% 基本事項A3.2.4:接線と弦のなす角(接弦定理)(One More)
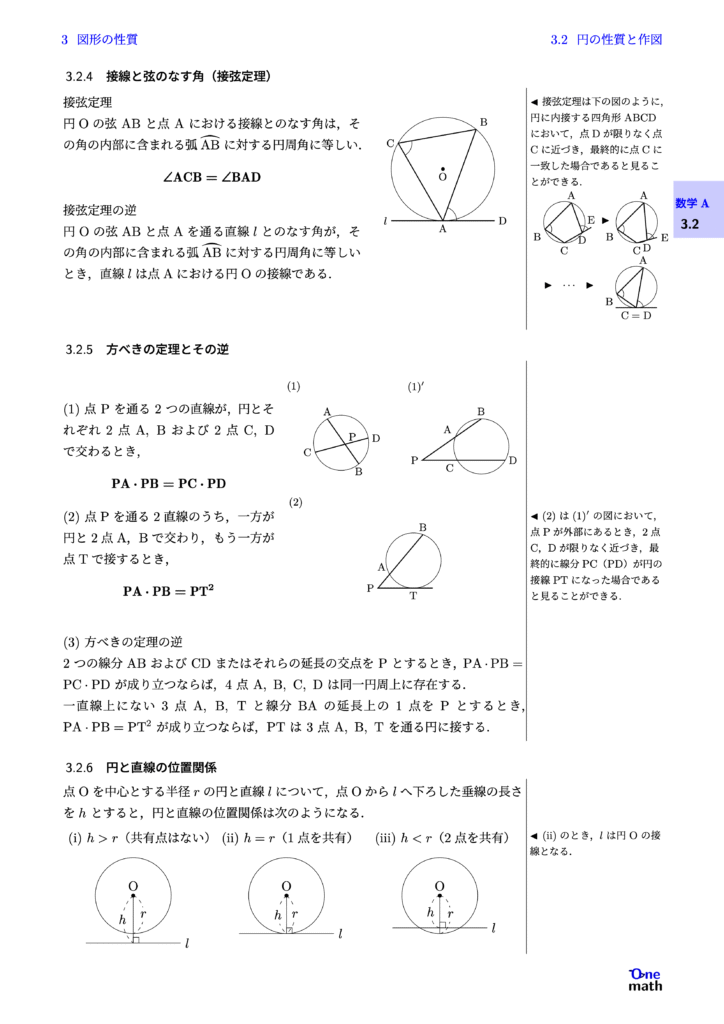
接弦定理 円Oの弦$\mathrm{AB}$と点$\mathrm{A}$における接線とのなす角は,その角の内部に含まれる弧$\wideparen{\mathrm{AB}}$に対する円周角に等し い. $$\angle\mathrm{ACB}=\angle\mathrm{BAD}$$ 接弦定理の逆 円Oの弦ABと点Aを通る直線$l$とのなす角が,その角の内部に含まれる弧$\wideparen{\mathrm{AB}}$に対する円周角に等しいとき,直線$l$は点Aにおける円Oの接線である.
% 基本事項A3.2.5:方べきの定理とその逆(One More)
(1)点$\mathrm{P}$を通る2つの直線が,円とそれぞれ2点$\mathrm{A},\mathrm{B}$および2点$\mathrm{C},\mathrm{D}$で交わるとき, $$ \mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD} $$ (2)点Pを通る2直線のうち,一方が円と2点A,Bで交わり,もう一方が点Tで接するとき, $$\mathrm{PA} \cdot \mathrm{PB}=\mathrm{PT}^2$$ (3)方べきの定理の逆 2つの線分$\mathrm{AB}$および$\mathrm{CD}$またはそれらの延長の交点を$\mathrm{P}$とするとき,$\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD}$が成り立つならば,4点$\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{D}$は同一円周上に存在する. 一直線上にない3点$\mathrm{A},\mathrm{B},\mathrm{T}$と線分$\mathrm{BA}$の延長上の1点を$\mathrm{P}$とするとき,$\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PT}^2$が成り立つならば,$\mathrm{PT}$は3点$\mathrm{A},\mathrm{B},\mathrm{T}$を通る円に接する.
% 基本事項A3.2.6:円と直線の位置関係(One More)
点Oを中心とする半径$r$の円と直線$l$について,点Oから$l$へ下ろした垂線の長さを$h$とすると,円と直線の位置関係は次のようになる. (i)$h>r$(共有点はない) (ii)$h=r$(1点を共有) (iii)$h<r$(2点を共有)
% 基本事項A3.2.7:2つの円の位置関係(One More)
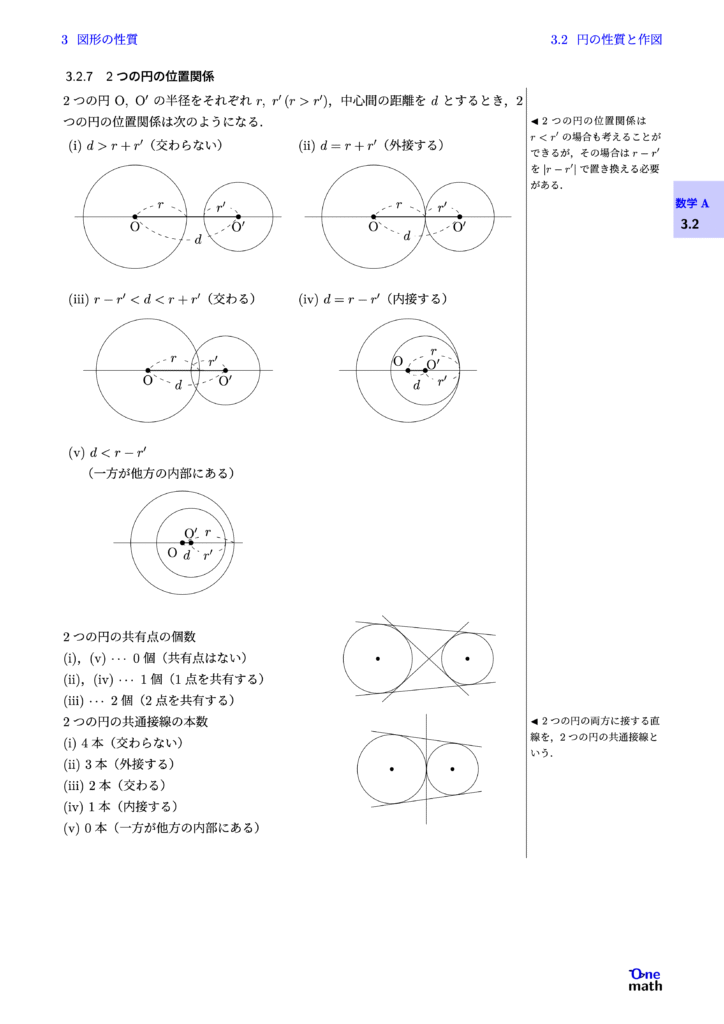
2つの円$\mathrm{O},\mathrm{O}^{\prime}$の半径をそれぞれ$r,r^{\prime}\left(r>r^{\prime}\right)$,中心間の距離を$d$とするとき,2つの円の位置関係は次のようになる. (i)$d>r+r^\prime$(交わらない) (ii)$d=r+r^\prime$(外接する) (iii)$r-r^\prime<d<r+r^\prime$(交わる) (iv)$d=r-r^\prime$(内接する) (v)$d<r-r^\prime$ (一方が他方の内部にある) 2つの円の共有点の個数 (i),(v)$\cdots$0個(共有点はない) (ii),(iv)$\cdots$1個(1点を共有する) (iii)$\cdots$2個(2点を共有する) 2つの円の共通接線の本数 (i)4本(交わらない) (ii)3本(外接する) (iii)2本(交わる) (iv)1本(内接する) (v)0本(一方が他方の内部にある)
% 基本事項A3.2.8:作図(One More)
定規とコンパスだけを用いて与えられた条件を満たす図形をかくことを作図という. 定規$\cdots$与えられた2点を通る直線を引く.また,線分を延長する. コンパス$\cdots$与えられた1点を中心として,与えられた半径の円をかく.
% 基本事項A3.2.9:基本作図(One More)
作図の手順 (i)求める図形が作図できたとして,それらを決定するための条件を解析し,作図の方法を考える(解析). (ii)求める図形の作図の手順を述べる(作図). (iii)作図によって得られた図形が条件を満たすことを確認する(証明). (1)直線外の点を通る直線の垂線 [1]点Pを中心として,直線$l$に交わる円をかき,直線$l$との交点をA,Bとする. [2]2点A,Bをそれぞれ中心とする等しい半径の円をかき,交点の1つをQとする. [3]直線PQを引く. (2)線分ABの垂直二等分線 [1]線分ABの両端の点A,Bをそれぞれ中心として,等しい半径の円をかく. [2][1]の2つの円の交点をP,Qとして,直線PQを引く.これが線分ABの垂直二等分線であり,その垂直二等分線と線分ABとの交点Mが線分ABの中点となる. (3)角の二等分線 [1]点Oを中心とする円をかき,線分OA,OBとの交点をそれぞれP,Qとする. [2]2点P,Qをそれぞれ中心とする等しい半径の円をかき,交点の1つをRとする. [3]直線ORを引く.これが$\angle\mathrm{AOB}$の二等分線となる. (4)直線外の点を通る直線の平行線 [1]直線$l$上に2点Q,Rをとる. [2]点Rを中心とする半径PQの円をかき,点Pを中心とする半径QRの円をかく.この2つの円の交点をSとする. [3]直線PSを引く.
% 基本事項A3.3.1:2直線間の位置関係(One More)
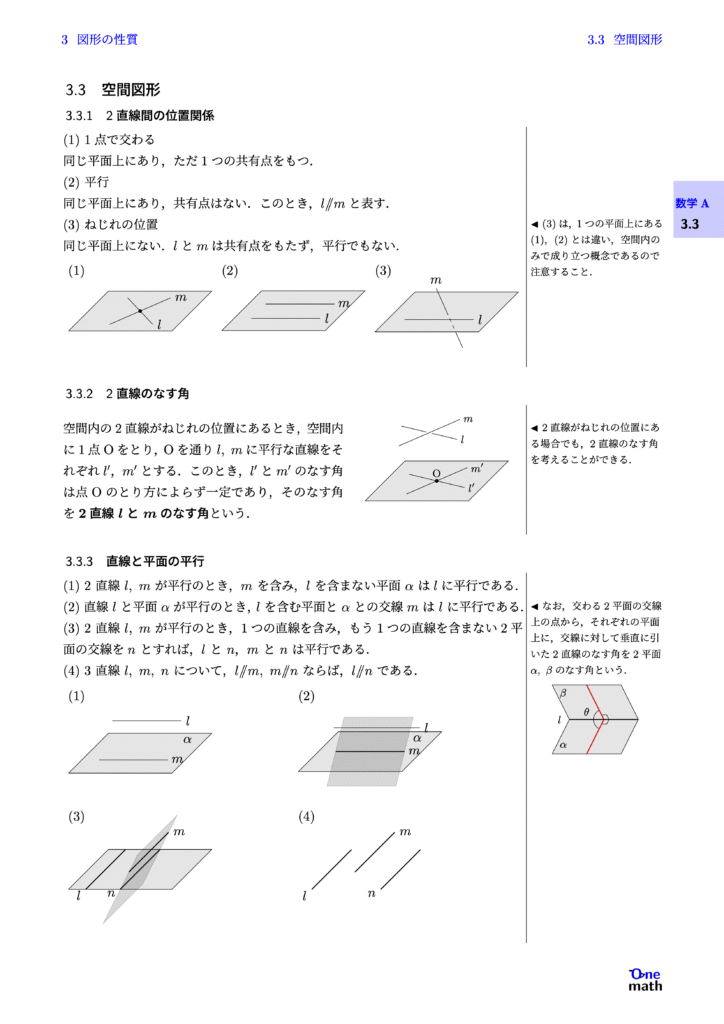
(1)1点で交わる 同じ平面上にあり,ただ1つの共有点をもつ. (2)平行 同じ平面上にあり,共有点はない.このとき,$l\parallel m$と表す. (3)ねじれの位置 同じ平面上にない.$l$と$m$は共有点をもたず,平行でもない.
% 基本事項A3.3.2:2直線のなす角(One More)
空間内の2直線がねじれの位置にあるとき,空間内に1点Oをとり,Oを通り$l,m$に平行な直線をそれぞれ$l^{\prime}$,$m^{\prime}$とする.このとき,$l^{\prime}$と$m^{\prime}$のなす角は点Oのとり方によらず一定であり,そのなす角を2直線$l$と$m$のなす角という.
% 基本事項A3.3.3:直線と平面の平行(One More)
(1)2直線$l,m$が平行のとき,$m$を含み,$l$を含まない平面$\alpha$は$l$に平行である. (2)直線$l$と平面$\alpha$が平行のとき,$l$を含む平面と$\alpha$との交線$m$は$l$に平行である. (3)2直線$l,m$が平行のとき,1つの直線を含み,もう1つの直線を含まない2平面の交線を$n$とすれば,$l$と$n$,$m$と$n$は平行である. (4)3直線$l,m,n$について,$ l \parallel m,m \parallel n $ ならば,$l \parallel n$である.
% 基本事項A3.3.4:直線と平面の垂直(One More)
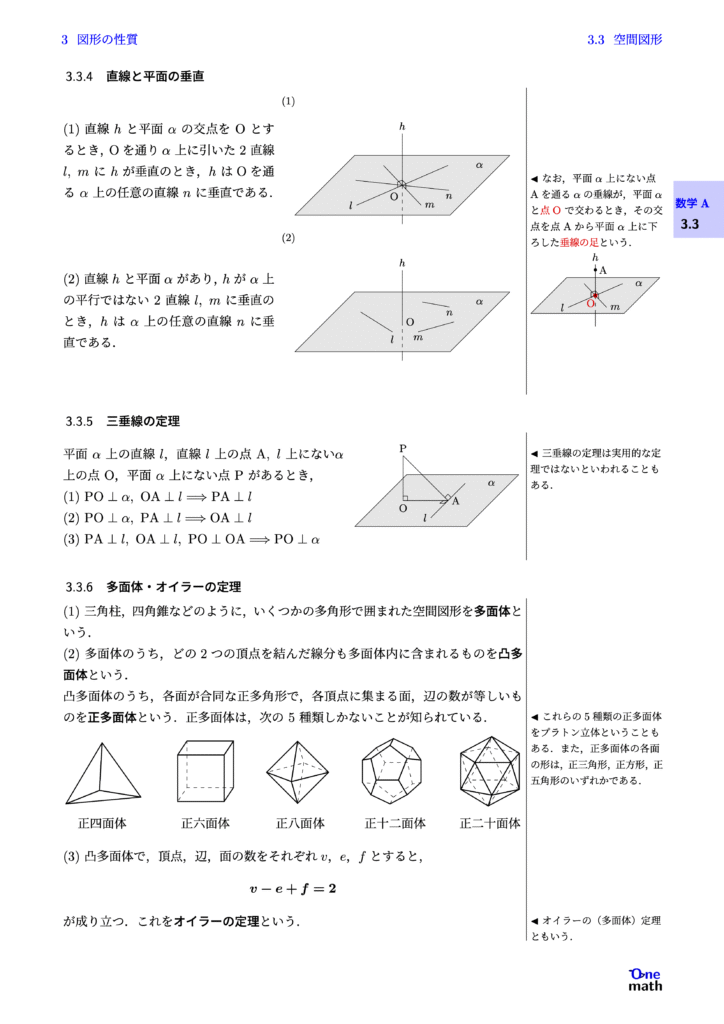
(1)直線$h$と平面$\alpha$の交点を$\mathrm{O}$とするとき,Oを通り$\alpha$上に引いた2直線$l,m$に$h$が垂直のとき,$h$はOを通る$\alpha$上の任意の直線$n$に垂直である. (2)直線$h$と平面$\alpha$があり,$h$が$\alpha$上の平行ではない2直線$l,m$に垂直のとき,$h$は$\alpha$上の任意の直線$n$に垂直である.
% 基本事項A3.3.5:三垂線の定理(One More)
平面$\alpha$上の直線$l$,直線$l$上の点$\mathrm{A},l$上にない$\alpha$上の点$\mathrm{O}$,平面$\alpha$上にない点$\mathrm{P}$があるとき, (1)$\mathrm{PO} \perp \alpha,\mathrm{O A} \perp l \Longrightarrow \mathrm{P A} \perp l$ (2)$\mathrm{PO} \perp \alpha,\mathrm{PA} \perp l \Longrightarrow \mathrm{OA} \perp l$ (3)$\mathrm{P A} \perp l,\mathrm{O A} \perp l,\mathrm{PO} \perp \mathrm{OA} \Longrightarrow \mathrm{PO} \perp \alpha$
% 基本事項A3.3.6:多面体・オイラーの定理(One More)
(1)三角柱,四角錐などのように,いくつかの多角形で囲まれた空間図形を多面体という. (2)多面体のうち,どの2つの頂点を結んだ線分も多面体内に含まれるものを凸多面体という. 凸多面体のうち,各面が合同な正多角形で,各頂点に集まる面,辺の数が等しいものを正多面体という.正多面体は,次の5種類しかないことが知られている. (3)凸多面体で,頂点,辺,面の数をそれぞれ$v$,$e$,$f$とすると, $$v-e+f=2$$ が成り立つ.これをオイラーの定理という.