問題の解答
検索用コード（LaTeX）
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 例題A3.2.1：円に内接する四角形（One More）★★
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
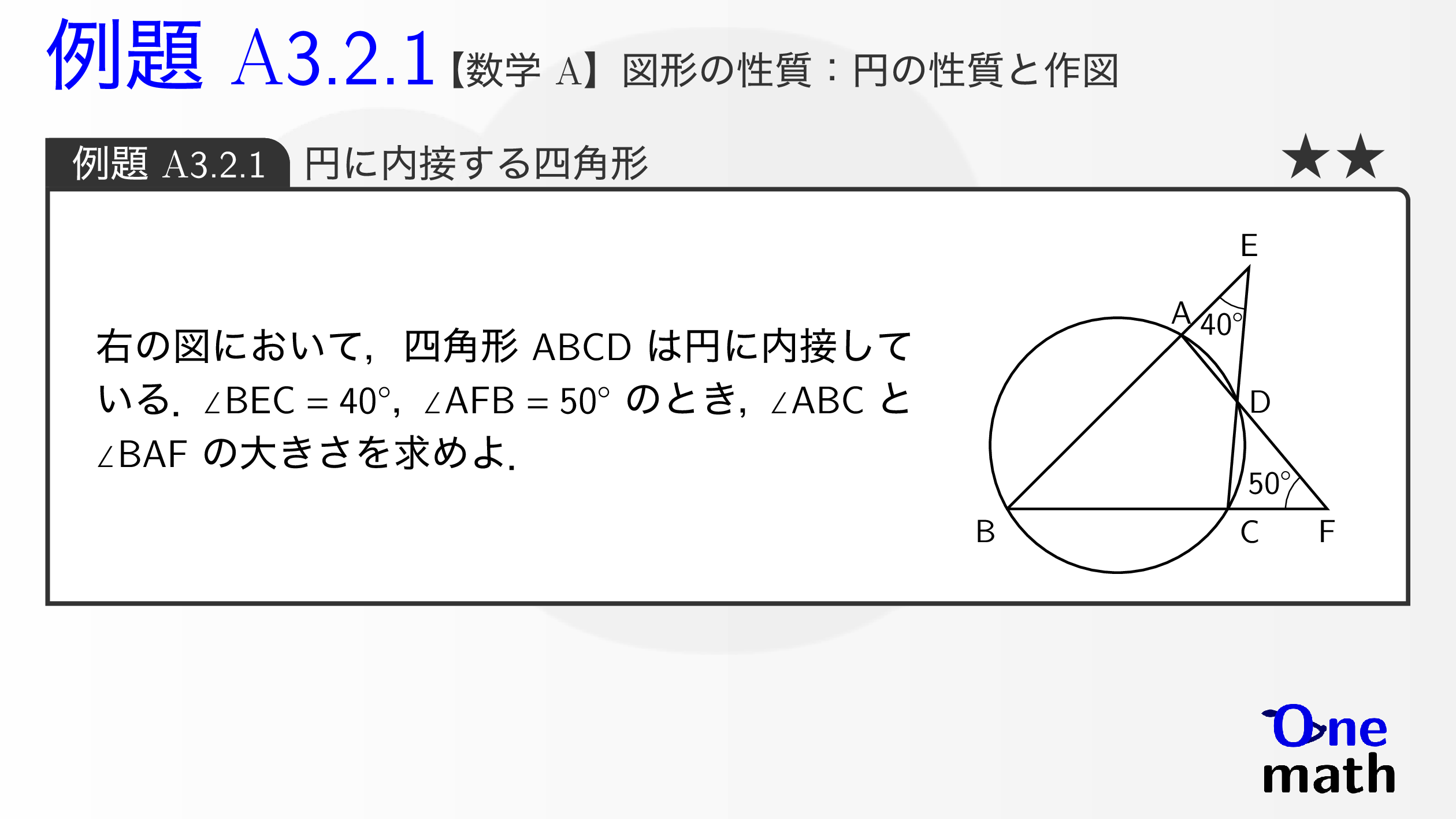
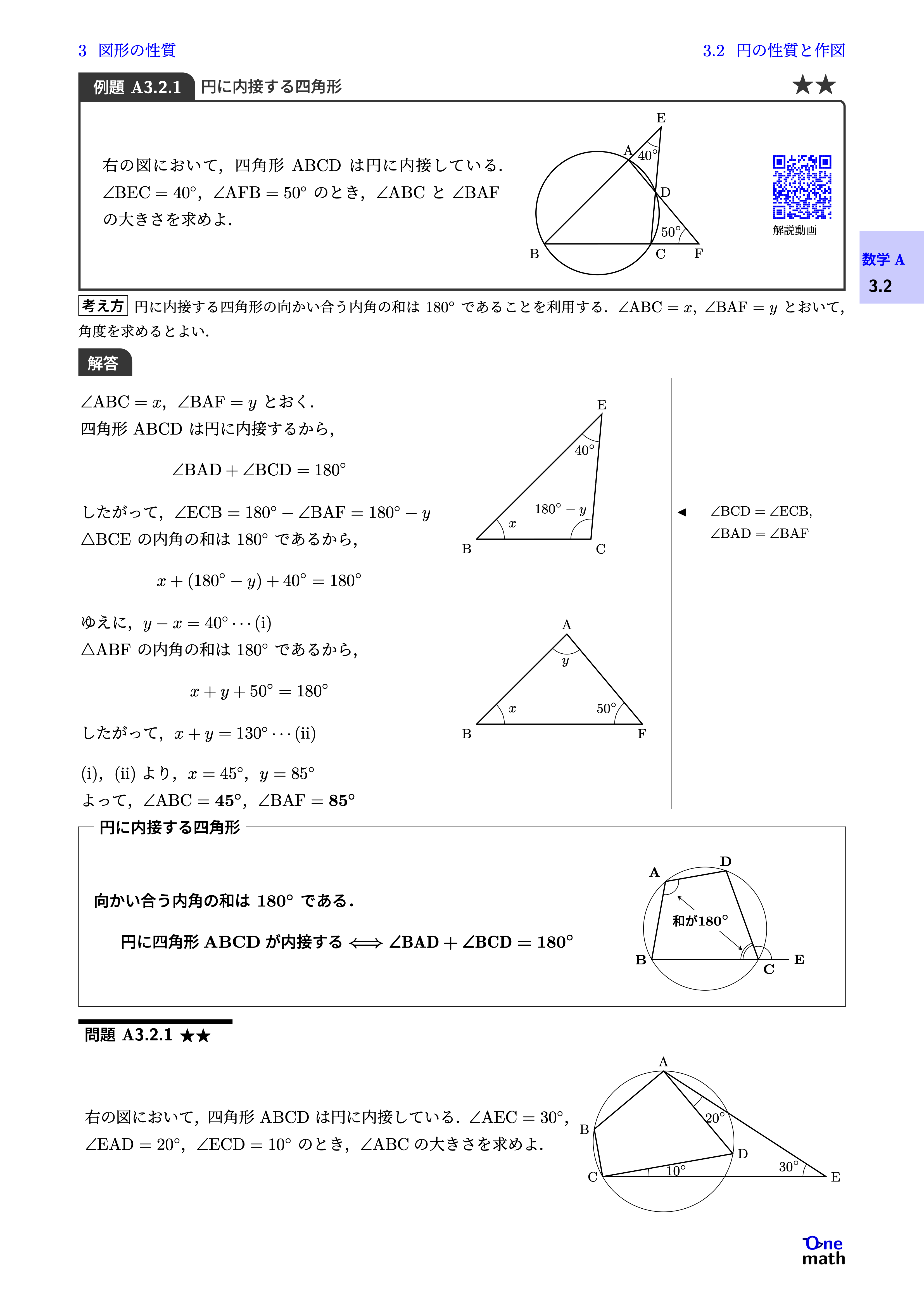
右の図において，四角形$\mathrm{ABCD}$は円に内接している．$\angle\mathrm{BEC}=40^{\circ}$，$\angle\mathrm{AFB}=50^{\circ}$のとき，$\angle\mathrm{ABC}$と$\angle\mathrm{BAF}$の大きさを求めよ．
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 例題A3.2.1の解答（One More）★★
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
$\angle\mathrm{ABC}=x$，$\angle\mathrm{BAF}=y$とおく．
四角形$\mathrm{ABCD}$は円に内接するから，
\[
\angle\mathrm{BAD}+\angle\mathrm{BCD}=180^{\circ}
\]
したがって，$\angle\mathrm{ECB}=180^{\circ}-\angle\mathrm{BAF}=180^{\circ}-y$
$\triangle\mathrm{BCE}$の内角の和は$180^{\circ}$であるから，
\[
x+(180^{\circ}-y)+40^{\circ}=180^{\circ}
\]
ゆえに，$y-x=40^{\circ}\cdots(\mathrm{i})$
$\triangle\mathrm{ABF}$の内角の和は$180^{\circ}$であるから，
\[
x+y+50^{\circ}=180^{\circ}
\]
したがって，$x+y=130^{\circ}\cdots(\mathrm{ii})$
(i)，(ii)より，$x=45^{\circ}$，$y=85^{\circ}$
よって，$\angle\mathrm{ABC}=45^{\circ}$，$\angle\mathrm{BAF}=85^{\circ}$
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 問題A3.2.1：円に内接する四角形（One More）★★
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
右の図において，四角形$\mathrm{ABCD}$は円に内接している．$\angle\mathrm{AEC}=30^{\circ}$，$\angle\mathrm{EAD}=20^{\circ}$，$\angle\mathrm{ECD}=10^{\circ}$のとき，$\angle\mathrm{ABC}$の大きさを求めよ．
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 問題A3.2.1の解答（One More）★★
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
四角形$\mathrm{ABCD}$は円に内接するから，$\angle\mathrm{BAD}+\angle\mathrm{BCD}=180^{\circ}$
四角形ABCEの内角の和は$360^\circ$であるから，
\[
\angle\mathrm{ABC}+180^{\circ}+20^{\circ}+30^{\circ}+10^{\circ}=360^{\circ}
\]
よって，$\angle\mathrm{ABC}=120^{\circ}$
あわせて読みたい
【数学A】3章：図形の性質（基本事項）
検索用コード（LaTeX） 本文・解答側注 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 基本事項A3.1.1：角（One More） %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%...
あわせて読みたい
【数学A】3章：図形の性質（節末問題・章末問題）
節末A3.1.1〜A3.1.4の解答 節末A3.1.1節末A3.1.2節末A3.1.3節末A3.1.4 リンク（関連例題） https://onemath.net/onemorea-reidai3-1-6 https://onemath.net/onemorea-re...