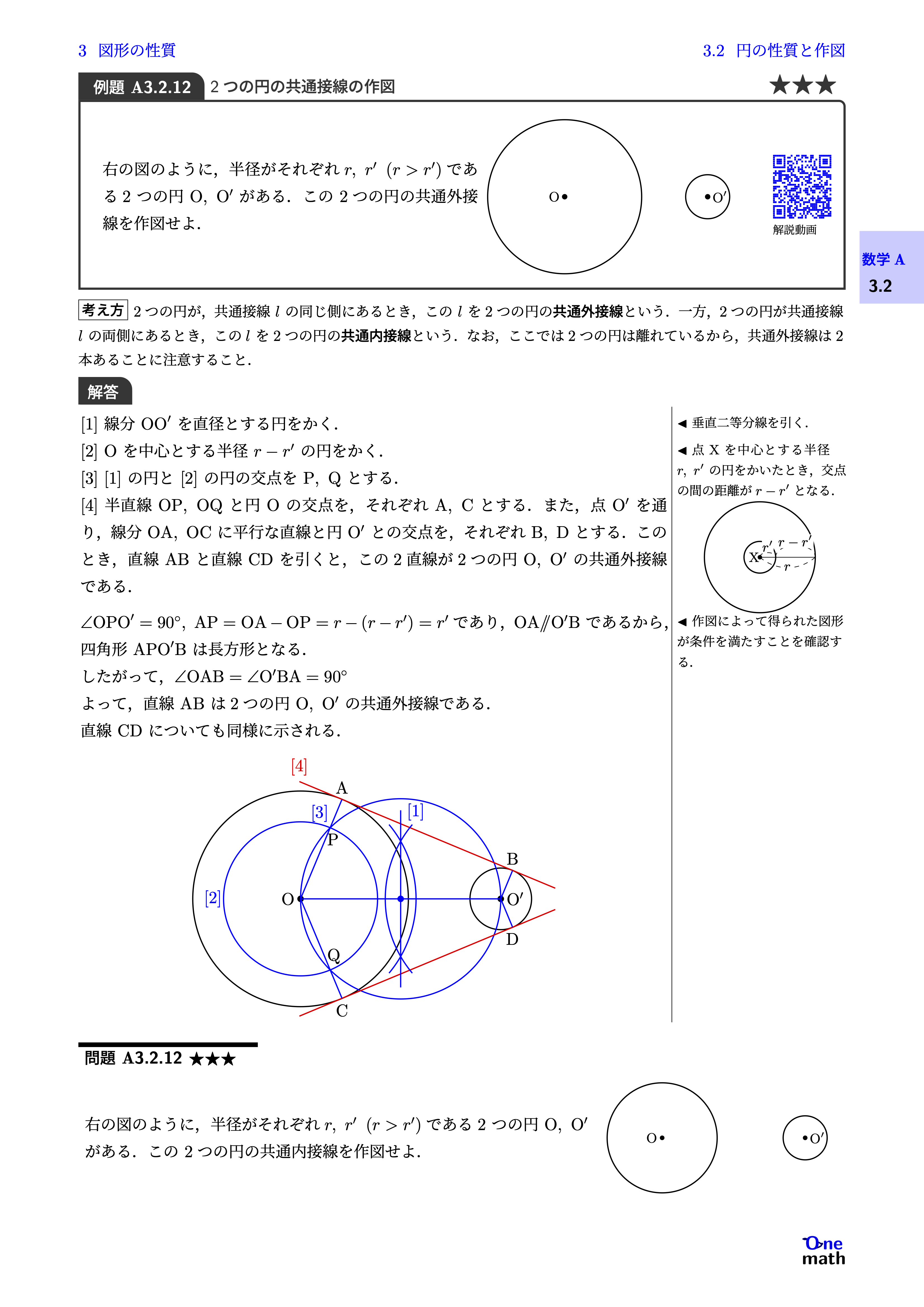
% 例題A3.2.12：2つの円の共通接線の作図 （One More）★★★
右の図のように,半径がそれぞれ$r,r^{\prime} \left(r>r^{\prime}\right)$である2つの円$\mathrm{O},\mathrm{O}^{\prime}$がある.この$2$つの円の共通外接線を作図せよ.
% 解答（例題A3.2.12）
[1]線分$\mathrm{OO}^{\prime}$を直径とする円をかく. [2]$\mathrm{O}$を中心とする半径$r-r^{\prime}$の円をかく. [3][1]の円と[2]の円の交点を$\mathrm{P},\mathrm{Q}$とする. [4]半直線$\mathrm{OP},\mathrm{OQ}$と円$\mathrm{O}$の交点を,それぞれ$\mathrm{A},\mathrm{C}$とする.また,点$\mathrm{O}^{\prime}$を通り,線分$\mathrm{OA},\mathrm{OC}$に平行な直線と円$\mathrm{O}^{\prime}$との交点を,それぞれ$\mathrm{B},\mathrm{D}$とする.このとき,直線$\mathrm{AB}$と直線$\mathrm{CD}$を引くと, この2直線が2つの円$\mathrm{O},\mathrm{O}^{\prime}$の共通外接線である.$\angle \mathrm{OPO}^{\prime}=90^{\circ}, \mathrm{AP}=\mathrm{OA}-\mathrm{OP}=r-(r-r^{\prime})=r^{\prime}$であり,$\mathrm{OA} \parallel \mathrm{O}^{\prime}\mathrm{B}$であるから,四角形$\mathrm{APO}^{\prime}\mathrm{B}$は長方形となる. したがって,$\angle \mathrm{OAB}=\angle \mathrm{O}^{\prime} \mathrm{BA}=90^{\circ}$よって,直線$\mathrm{AB}$は2つの円$\mathrm{O},\mathrm{O}^{\prime}$の共通外接線である. 直線$\mathrm{CD}$についても同様に示される.
% 問題A3.2.12
右の図のように,半径がそれぞれ$r,r^{\prime} \left(r>r^{\prime}\right)$である2つの円$\mathrm{O},\mathrm{O}^{\prime}$がある.この$2$つの円の共通内接線を作図せよ.
% 解答A3.2.12
[1]線分$\mathrm{OO}^{\prime}$を直径とする円をかく. [2]$\mathrm{O}$を中心とする半径$r+r^{\prime}$の円をかく. [3][1]の円と[2]の円の交点を$\mathrm{P},\mathrm{Q}$とする. [4]半直線$\mathrm{OP},\mathrm{OQ}$と円$\mathrm{O}$の交点を,それぞれ$\mathrm{A},\mathrm{C}$とする.また,点$\mathrm{O}^{\prime}$を通り,線分$\mathrm{OA},\mathrm{OC}$に平行な直線と円$\mathrm{O}^{\prime}$との交点を,それぞれ$\mathrm{B},\mathrm{D}$とする.このとき,直線$\mathrm{AB}$と直線$\mathrm{CD}$を引くと, この2直線が2つの円$\mathrm{O},\mathrm{O}^{\prime}$の共通内接線である.$\angle \mathrm{OPO}^{\prime}=90^{\circ}, \mathrm{AP}=\mathrm{OP}-\mathrm{OA}=(r+r^{\prime})-r=r^{\prime}$であり,$\mathrm{OA} \parallel \mathrm{O}^{\prime}\mathrm{B}$であるから,四角形$\mathrm{APO}^{\prime}\mathrm{B}$は長方形となる. したがって,$\angle \mathrm{OAB}=\angle \mathrm{O}^{\prime} \mathrm{BA}=90^{\circ}$よって,直線$\mathrm{AB}$は2つの円$\mathrm{O},\mathrm{O}^{\prime}$の共通内接線である. 直線$\mathrm{CD}$についても同様に示される.
