% 例題A3.2.8：互いに接する円 （One More）★★
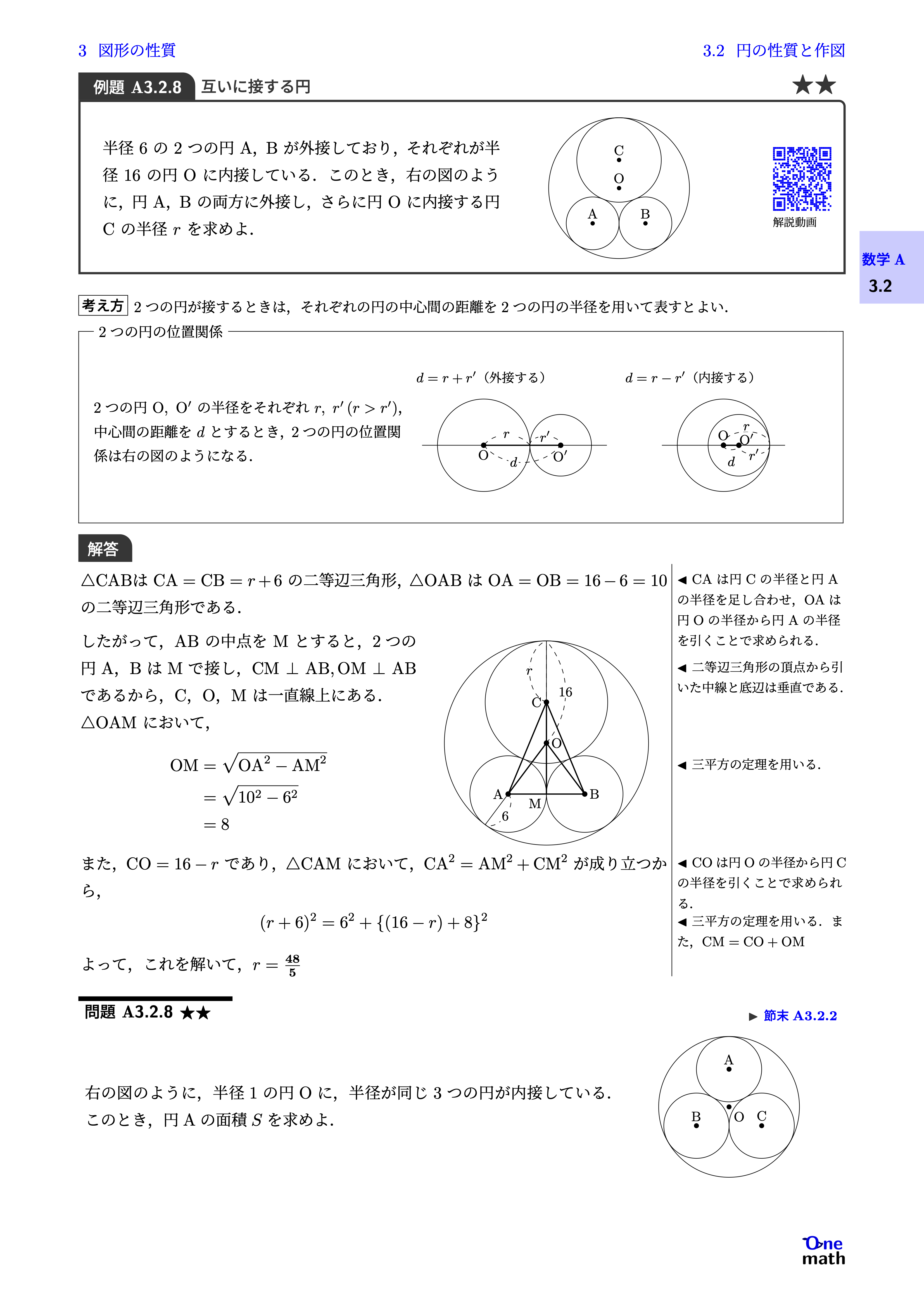
半径$6$の$2$つの円$\mathrm{A}$,$\mathrm{B}$が外接しており,それぞれが半径$16$の円$\mathrm{O}$に内接している.このとき,右の図のように,円$\mathrm{A}$,$\mathrm{B}$の両方に外接し,さらに円$\mathrm{O}$に内接する円$\mathrm{C}$の半径$r$を求めよ.
% 解答（例題A3.2.8）
$\triangle \mathrm{CAB}$は$\mathrm{CA}=\mathrm{CB}=r+6$の二等辺三角形,$\triangle \mathrm{OAB}$は$\mathrm{OA}=\mathrm{OB}=16-6=10$の二等辺三角形である. したがって,ABの中点をMとすると,2つの円A,BはMで接し,$\mathrm{CM} \perp \mathrm{AB},\mathrm{OM} \perp \mathrm{AB}$であるから,C,O,Mは一直線上にある.$\triangle \mathrm{OAM}$において,$$\begin{aligned} \mathrm{OM} &=\sqrt{\mathrm{OA}^2-\mathrm{AM}^2} \\ &=\sqrt{10^2-6^2} \\ &=8 \end{aligned}$$また,$\mathrm{CO}=16-r$であり,$\triangle \mathrm{CAM}$において,$\mathrm{CA}^2=\mathrm{AM}^2+\mathrm{CM}^2$が成り立つから,$$(r+6)^2=6^2+\{(16-r)+8\}^2$$よって,これを解いて,$r=\frac{48}{5}$
% 問題A3.2.8
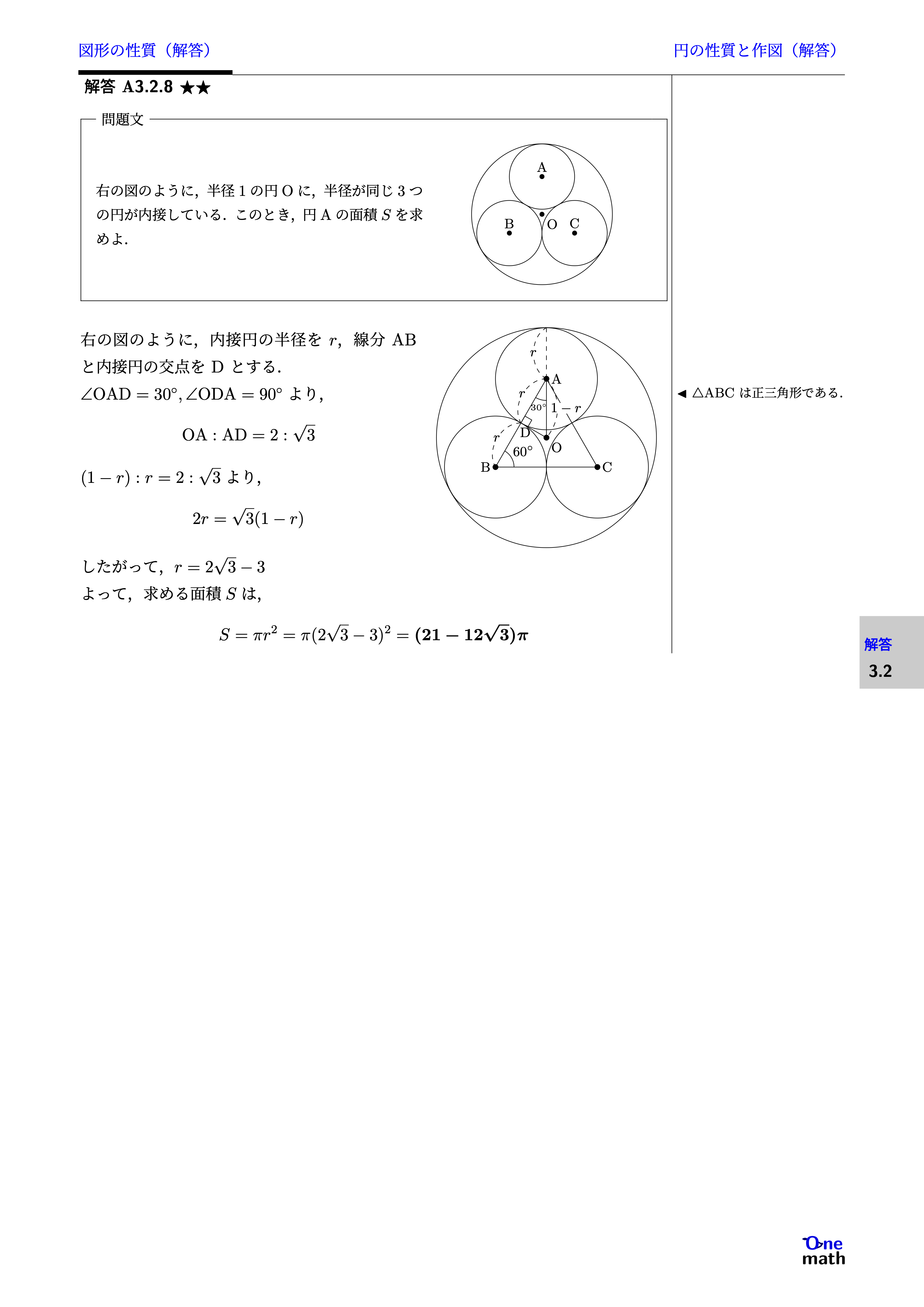
右の図のように,半径1の円Oに,半径が同じ3つの円が内接している.このとき,円Aの面積$S$を求めよ.
% 解答A3.2.8
右の図のように,内接円の半径を$r$,線分ABと内接円の交点をDとする.$\angle \mathrm{OAD}=30^{\circ},\angle \mathrm{ODA}=90^{\circ}$より,$$\mathrm{OA}: \mathrm{AD}=2: \sqrt{3}$$$(1-r): r=2: \sqrt{3}$より,$$2 r=\sqrt{3}(1-r)$$したがって,$r=2 \sqrt{3}-3$よって,求める面積$S$は,$$S=\pi r^2=\pi(2 \sqrt{3}-3)^2=(21-12 \sqrt{3})\pi$$
