【数学A】例題3.3.2：三垂線の定理（One More）★★★

% 例題A3.3.2：三垂線の定理 （One More）★★★
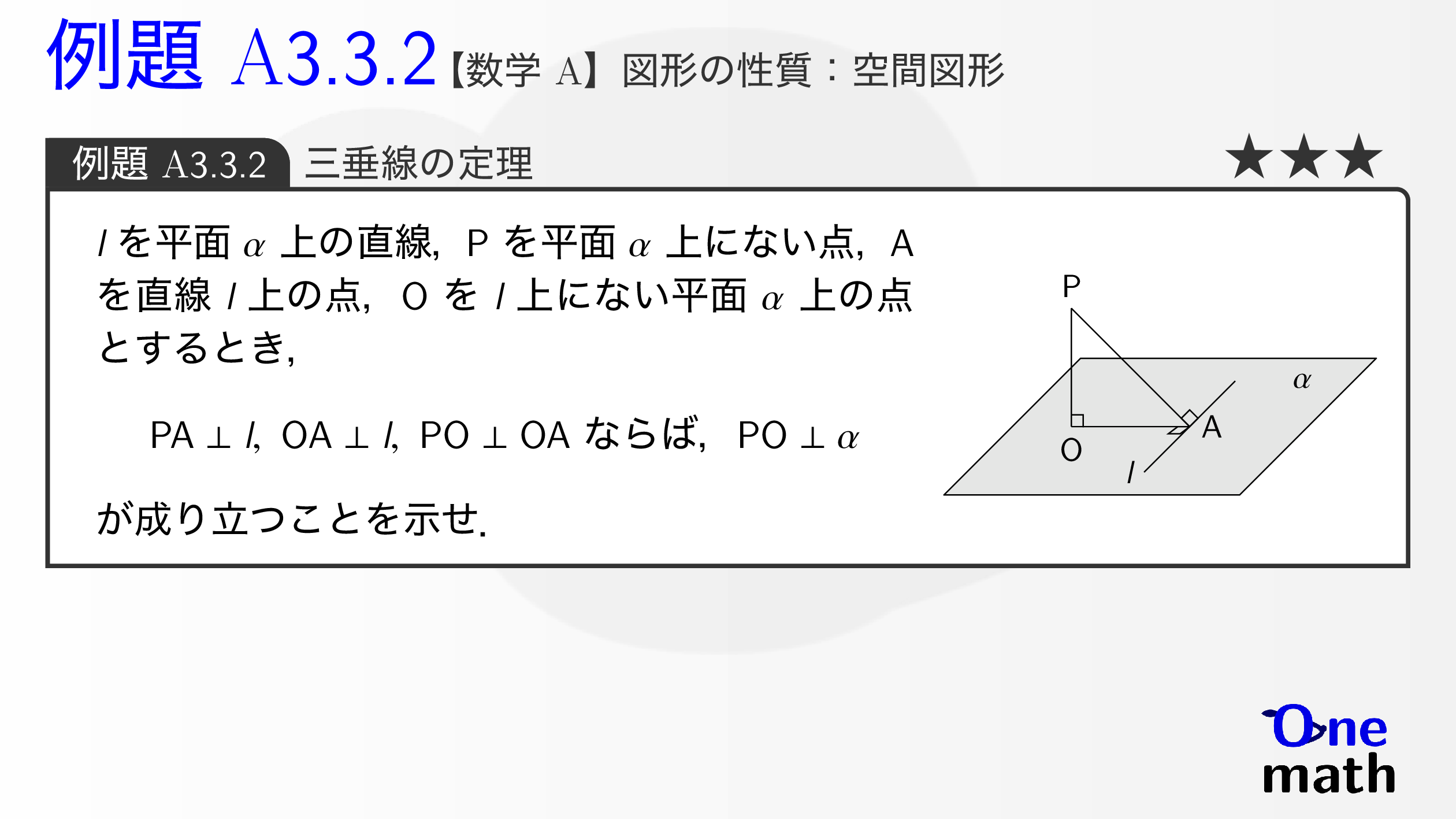
$l$を平面$\alpha$上の直線,$\mathrm{P}$を平面$\alpha$上にない点,$\mathrm{A}$を直線$l$上の点,$\mathrm{O}$を$l$上にない平面$\alpha$上の点とするとき, \begin{center}$\mathrm{PA} \perp l,\mathrm{OA} \perp l,\mathrm{PO} \perp \mathrm{OA}$ならば,$\mathrm{PO} \perp \alpha$\end{center} が成り立つことを示せ.

% 解答（例題A3.3.2）
$\mathrm{PA} \perp l,\mathrm{OA} \perp l$より,$l$は平面$\mathrm{AOP}$上の交わる2直線$\mathrm{PA}$,$\mathrm{OA}$に垂直であるから,$l \perp$平面$\mathrm{AOP}$$\mathrm{PO}$は平面$\mathrm{AOP}$上にあるから,$$\mathrm{PO} \perp l \cdots (\mathrm{i})$$また,仮定より,$\mathrm{PO} \perp \mathrm{OA} \cdots (\mathrm{ii})$よって,(i),(ii)より,直線$\mathrm{PO}$は平面$\alpha$上の交わる2直線$l$,$\mathrm{OA}$と垂直であるから,$\mathrm{PO} \perp \alpha \blacksquare$別解： 直線$l$上に,$\mathrm{A}$と異なる点$\mathrm{B}$をとる. 三平方の定理より,$$\begin{aligned} & \mathrm{PA}^2+\mathrm{AB}^2=\mathrm{PB}^2 \cdots (\mathrm{i}),\\ & \mathrm{OA}^2+\mathrm{AB}^2=\mathrm{OB}^2 \cdots (\mathrm{ii}),\\ & \mathrm{PO}^2+\mathrm{OA}^2=\mathrm{PA}^2 \cdots (\mathrm{iii}) \end{aligned}$$(i)〜(iii)より,$$\mathrm{PO}^2+\mathrm{OB}^2=\mathrm{PB}^2$$三平方の定理の逆より,$\angle \mathrm{POB}=90^{\circ}$,すなわち,$\mathrm{PO} \perp \mathrm{OB} \cdots (\mathrm{iv})$また,仮定より,$\mathrm{PO} \perp \mathrm{OA} \cdots (\mathrm{v})$よって,(iv),(v)より,直線$\mathrm{PO}$は平面$\alpha$上の交わる2直線$\mathrm{OB}$,$\mathrm{OA}$と垂直であるから,$\mathrm{PO} \perp \alpha \blacksquare$

% 問題A3.3.2
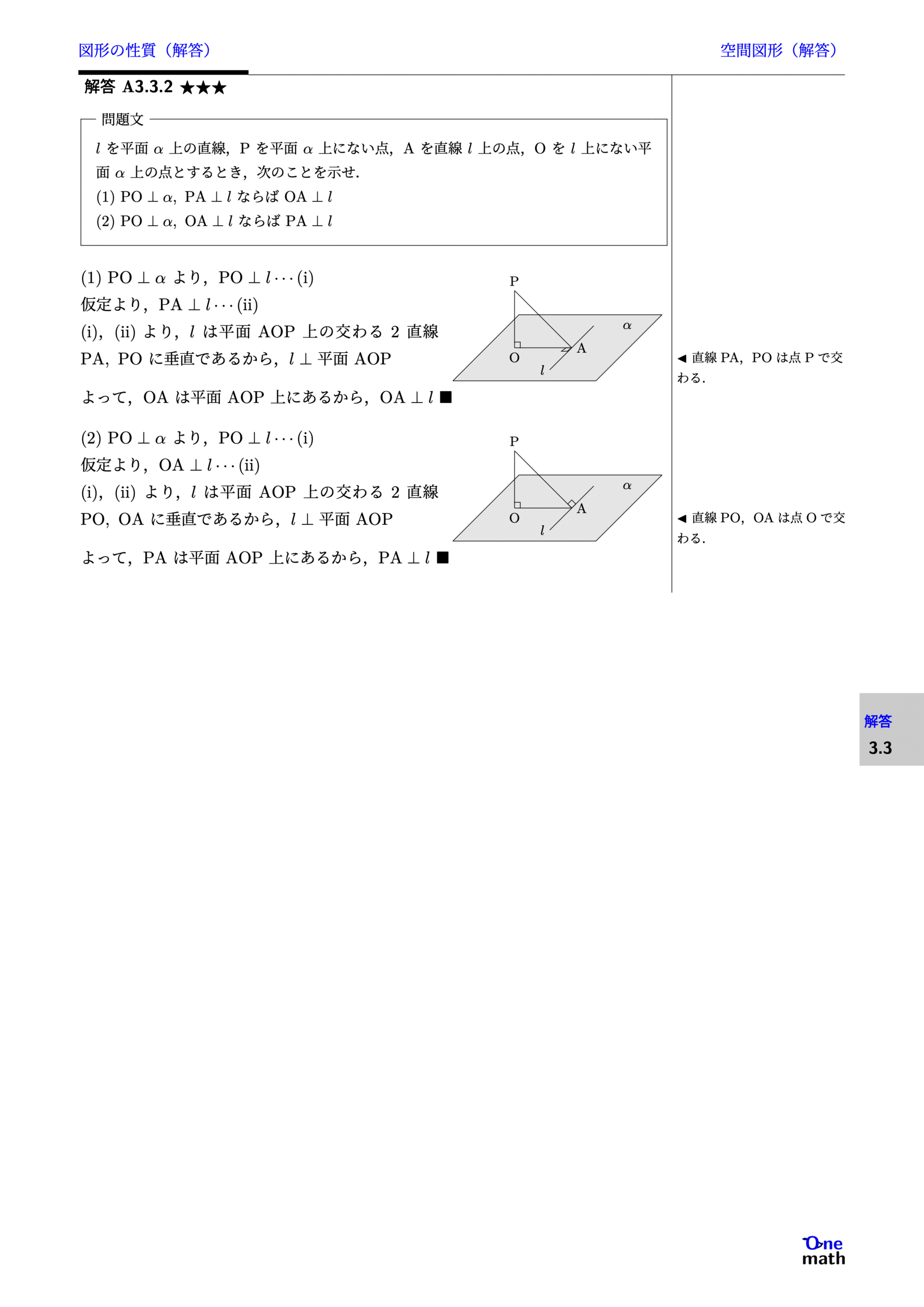
$l$を平面$\alpha$上の直線,$\mathrm{P}$を平面$\alpha$上にない点,$\mathrm{A}$を直線$l$上の点,$\mathrm{O}$を$l$上にない平面$\alpha$上の点とするとき,次のことを示せ. (1)$\mathrm{PO} \perp \alpha,\mathrm{PA} \perp l$ならば$\mathrm{OA} \perp l$(2)$\mathrm{PO} \perp \alpha,\mathrm{OA} \perp l$ならば$\mathrm{PA} \perp l$

% 解答A3.3.2
(1)$\mathrm{PO} \perp \alpha$より$\mathrm{PO} \perp l \cdots (\mathrm{i})$仮定より,$\mathrm{PA} \perp l \cdots (\mathrm{ii})$(i),(ii)より,$l$は平面$\mathrm{AOP}$上の交わる2直線$\mathrm{PA},\mathrm{PO}$に垂直であるから,$l \perp \text{平面} \mathrm{AOP}$よって,$\mathrm{OA}$は平面$\mathrm{AOP}$上にあるから,$\mathrm{OA} \perp l \blacksquare$(2)$\mathrm{PO} \perp \alpha$より,$\mathrm{PO} \perp l \cdots (\mathrm{i})$仮定より,$\mathrm{OA} \perp l \cdots (\mathrm{ii})$(i),(ii)より,$l$は平面$\mathrm{AOP}$上の交わる2直線$\mathrm{PO},\mathrm{OA}$に垂直であるから,$l \perp \text{平面} \mathrm{AOP}$よって,$\mathrm{PA}$は平面$\mathrm{AOP}$上にあるから,$\mathrm{PA} \perp l \blacksquare$