【数学I】例題4.1.15：三角比を含む方程式の解の個数1（One More）★★★★

% 例題I4.1.15：三角比を含む方程式の解の個数1 （One More）★★★★
方程式$2 \cos ^2 \theta+\sin \theta-a=0 \left(0^{\circ} \leqq \theta \leqq 180^{\circ}\right)$を満たす$\theta$が異なる2個の解をもつような定数$a$の値の範囲を求めよ.

% 解答（例題I4.1.15）
$\sin \theta=t$とおくと,$\sin^2\theta+\cos^2\theta=1$より,与えられた方程式は,$-2t^2+t+2-a=0 \cdots (\mathrm{i})$0^{\circ} \leqq \theta \leqq 180^{\circ}$のとき,$t$の値の範囲は$0 \leqq t \leqq 1$であり,$0 \leqq t<1$のとき,$\sin \theta=t$を満たす$\theta$の値は2個,$t=1$のとき,$\sin \theta=1$を満たす$\theta$の値は1個である. したがって,与えられた方程式を満たす$\theta$が$0^{\circ} \leqq \theta \leqq 180^{\circ}$の範囲で異なる2個の解をもつのは,(i)が$0 \leqq t<1$の範囲で解を1個もつときである. (i)を整理すると,$a=-2t^2+t+2$ゆえに,$a=-2\left(t-\frac{1}{4}\right)^2+\frac{17}{8} \cdots (\mathrm{ii})$(ii)の実数解の個数は,$y=a$と$y=-2\left(t-\frac{1}{4}\right)^2+\frac{17}{8}$のグラフの共有点の個数と一致する. よって,右の図より,$0 \leqq t<1$の範囲で解を1個もつ$a$の範囲は,$1<a<2,a=\frac{17}{8}$

% 問題I4.1.15
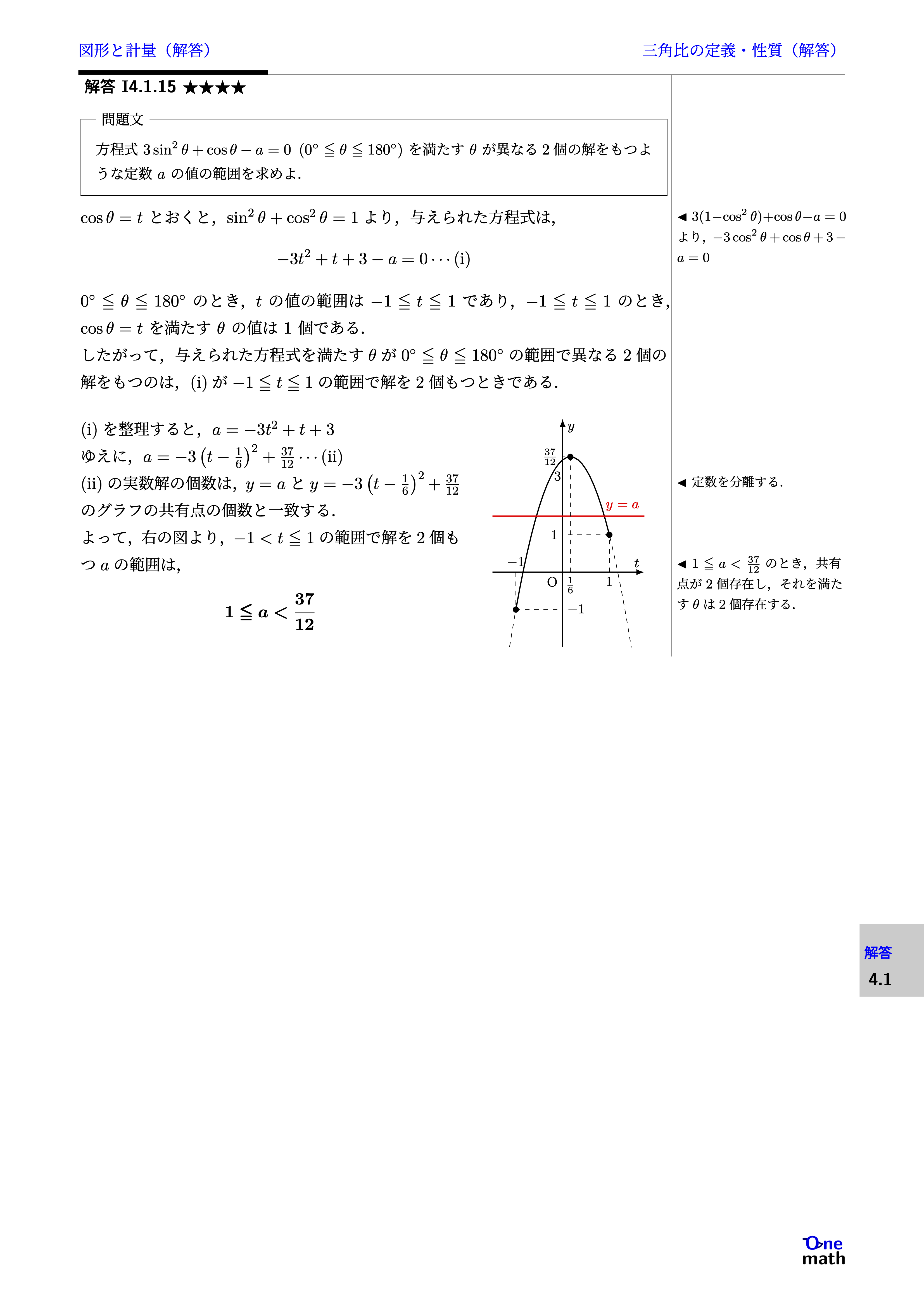
方程式$3 \sin ^2 \theta+\cos \theta-a=0 \left(0^{\circ} \leqq \theta \leqq 180^{\circ}\right)$を満たす$\theta$が異なる2個の解をもつような定数$a$の値の範囲を求めよ.

% 解答I4.1.15
$\cos \theta=t$とおくと,$\sin^2\theta+\cos^2\theta=1$より,与えられた方程式は,$-3t^2+t+3-a=0 \cdots (\mathrm{i})$0^{\circ} \leqq \theta \leqq 180^{\circ}$のとき,$t$の値の範囲は$-1 \leqq t \leqq 1$であり,$-1 \leqq t \leqq 1$のとき,$\cos \theta=t$を満たす$\theta$の値は1個である. したがって,与えられた方程式を満たす$\theta$が$0^{\circ} \leqq \theta \leqq 180^{\circ}$の範囲で異なる2個の解をもつのは,(i)が$-1 \leqq t \leqq 1$の範囲で解を2個もつときである. (i)を整理すると,$a=-3t^2+t+3$ゆえに,$a=-3\left(t-\frac{1}{6}\right)^2+\frac{37}{12} \cdots (\mathrm{ii})$(ii)の実数解の個数は,$y=a$と$y=-3\left(t-\frac{1}{6}\right)^2+\frac{37}{12}$のグラフの共有点の個数と一致する. よって,右の図より,$-1