% 例題I2.1.8：命題の真偽と集合 （One More）★
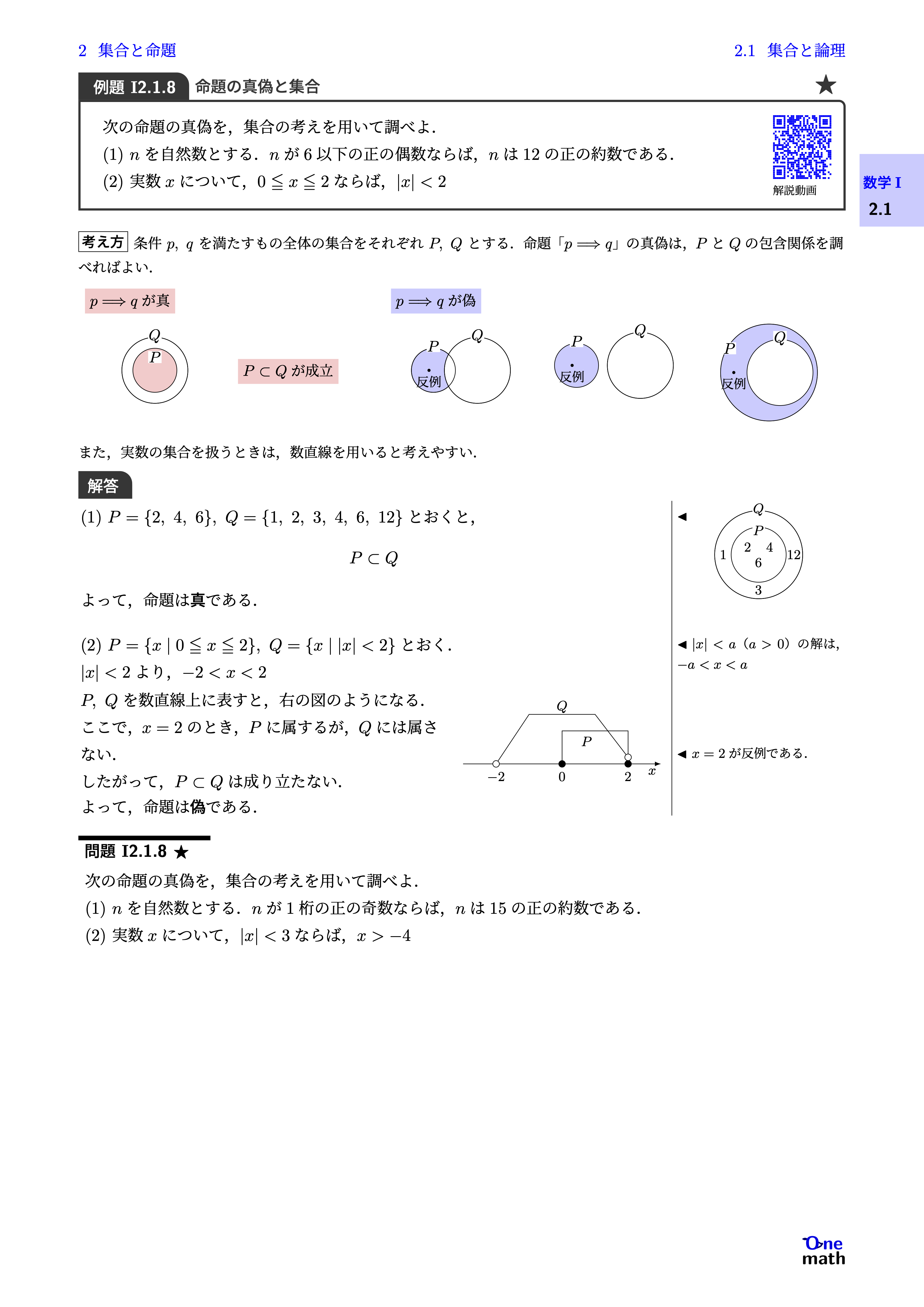
次の命題の真偽を,集合の考えを用いて調べよ. (1)$n$を自然数とする.$n$が6以下の正の偶数ならば,$n$は12の正の約数である. (2)実数$x$について,$0 \leqq x \leqq 2$ならば,$|x|<2$
% 解答（例題I2.1.8）
(1)$P=\{2,4,6\},Q=\{1,2,3,4,6,12\}$とおくと,$$P\subset Q$$よって,命題は真である. (2)$P=\{x \mid 0 \leqq x \leqq 2\},Q=\{x \mid|x|<2\}$とおく.$|x|<2$より,$-2<x<2$$P,Q$を数直線上に表すと,右の図のようになる. ここで,$x=2$のとき,$P$に属するが,$Q$には属さない. したがって,$P\subset Q$は成り立たない. よって,命題は偽である.
% 問題I2.1.8
次の命題の真偽を,集合の考えを用いて調べよ. (1)$n$を自然数とする.$n$が1桁の正の奇数ならば,$n$は15の正の約数である. (2)実数$x$について,$|x|<3$ならば,$x>-4$
% 解答I2.1.8
(1)$P=\{1,3,5,7,9\},Q=\{1,3,5,15\}$とおくと,$7\notin Q$であるから,$P \subset Q$は成り立たない. よって,命題は偽である. (2)$P=\{x \mid |x|<3\},Q=\{x \mid x>-4\}$とおく.$|x|<3$より,$-3<x<3$$P,Q$を数直線上に表すと,右の図のようになる. したがって,$P\subset Q$が成り立つ. よって,命題は真である.
