% 例題I3.1.4：2次関数のグラフ1 （One More）★
次の2次関数のグラフは,2次関数$y=2x^2$のグラフをそれぞれどのように平行移動したものか.また,それぞれのグラフをかき,その軸と頂点を求めよ. (1)$y=2x^2-1$(2)$y=2(x+1)^2$(3)$y=2(x-1)^2+1$
% 解答（例題I3.1.4）
(1)$y$軸方向に$-1$だけ平行移動したものであり,グラフは右の図のようになる. 軸は$y$軸（直線$x=0$） 頂点は点$(0,-1)$(2)$x$軸方向に$-1$だけ平行移動したものであり,グラフは右の図のようになる. 軸は直線$x=-1$頂点は点$(-1,0)$(3)$x$軸方向に$1,y$軸方向に1だけ平行移動したものであり,グラフは右の図のようになる. 軸は直線$x=1$頂点は点$(1,1)$
% 問題I3.1.4
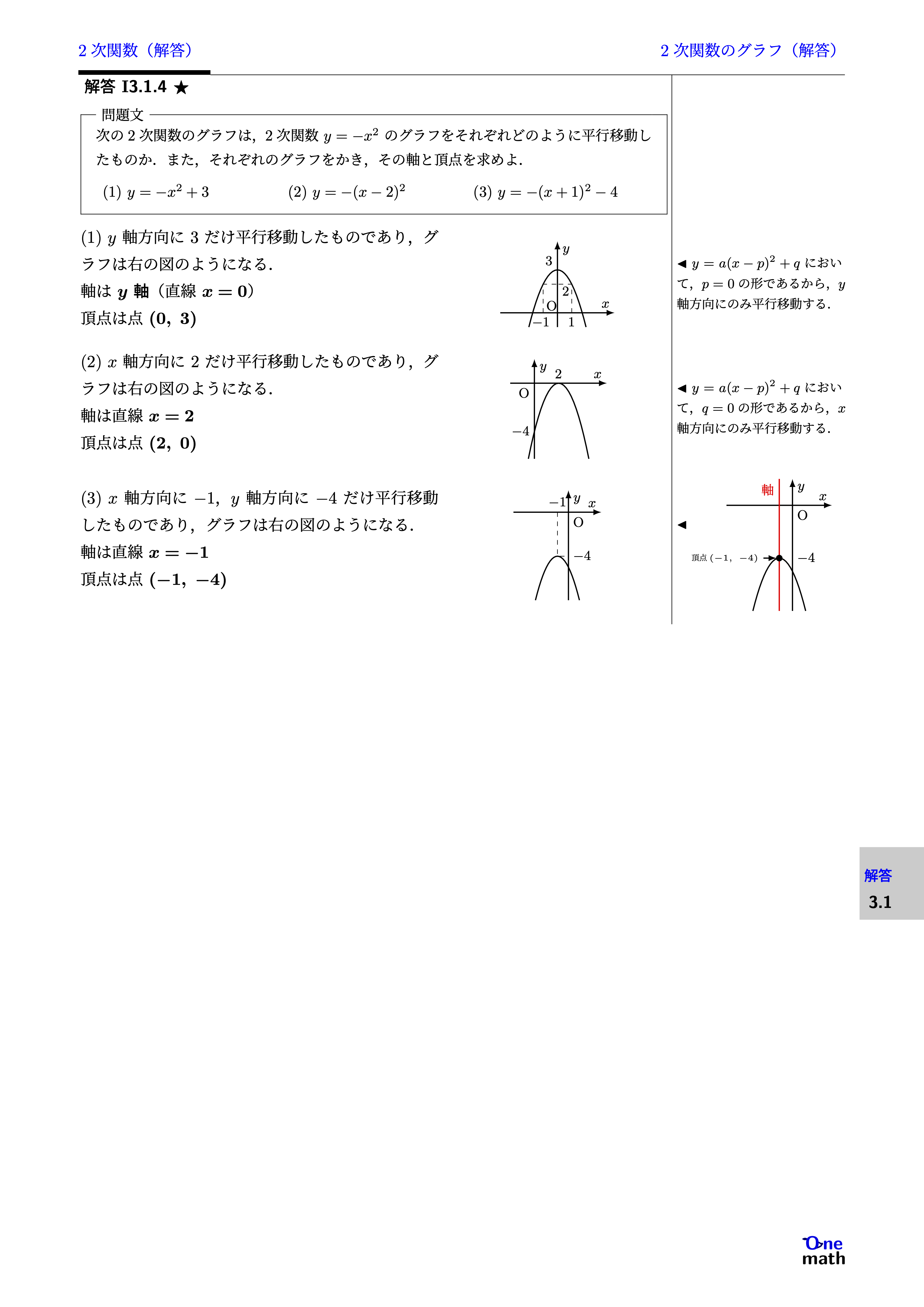
次の2次関数のグラフは,2次関数$y=-x^2$のグラフをそれぞれどのように平行移動したものか.また,それぞれのグラフをかき,その軸と頂点を求めよ. (1)$y=-x^2+3$(2)$y=-(x-2)^2$(3)$y=-(x+1)^2-4$
% 解答I3.1.4
(1)$y$軸方向に$3$だけ平行移動したものであり,グラフは右の図のようになる. 軸は$y$軸（直線$x=0$） 頂点は点$(0,3)$(2)$x$軸方向に$2$だけ平行移動したものであり,グラフは右の図のようになる. 軸は直線$x=2$頂点は点$(2,0)$(3)$x$軸方向に$-1,y$軸方向に$-4$だけ平行移動したものであり,グラフは右の図のようになる. 軸は直線$x=-1$頂点は点$(-1,-4)$
