% 例題I3.2.3：最大・最小による係数の決定 （One More）★★★
関数$f(x)=a x^2-4 a x+2b(-1 \leqq x \leqq 3)$の最大値が$7$,最小値が$-2$のとき,定数$a,b$の値を求めよ.
% 解答（例題I3.2.3）
$f(x)=a x^2-4 a x+2b =a(x-2)^2-4 a+2b$(i)$a>0$のとき$y=f(x)$のグラフは下に凸の放物線で,$-1 \leqq x \leqq 3$の範囲で$f(x)$は,$x=-1$のとき,最大値$5a+2b,x=2$のとき,最小値$-4a+2b$をとる. したがって,$\left\{\begin{array}{l} 5 a+2b=7 \\-4 a+2b=-2\end{array}\right.$ゆえに,$a=1,b=1$これは$a>0$を満たす. (ii)$a=0$のとき$f(x)=b$で一定の値をとり,最大値7,最小値$-2$をとることはないから,不適である. (iii)$a<0$のとき$y=f(x)$のグラフは上に凸の放物線で,$-1 \leqq x \leqq 3$の範囲で$f(x)$は,$x=2$のとき,最大値$-4a+2b,x=-1$のとき,最小値$5a+2b$をとる. したがって,$\left\{\begin{array}{l}-4a+2b=7 \\ 5a+2b=-2\end{array}\right.$ゆえに,$a=-1,b=\frac{3}{2}$これは$a<0$を満たす. よって,(i)〜(iii)より,求める$a,b$の値は,$(a,b)=(1,1),(-1,\frac{3}{2})$
% 問題I3.2.3
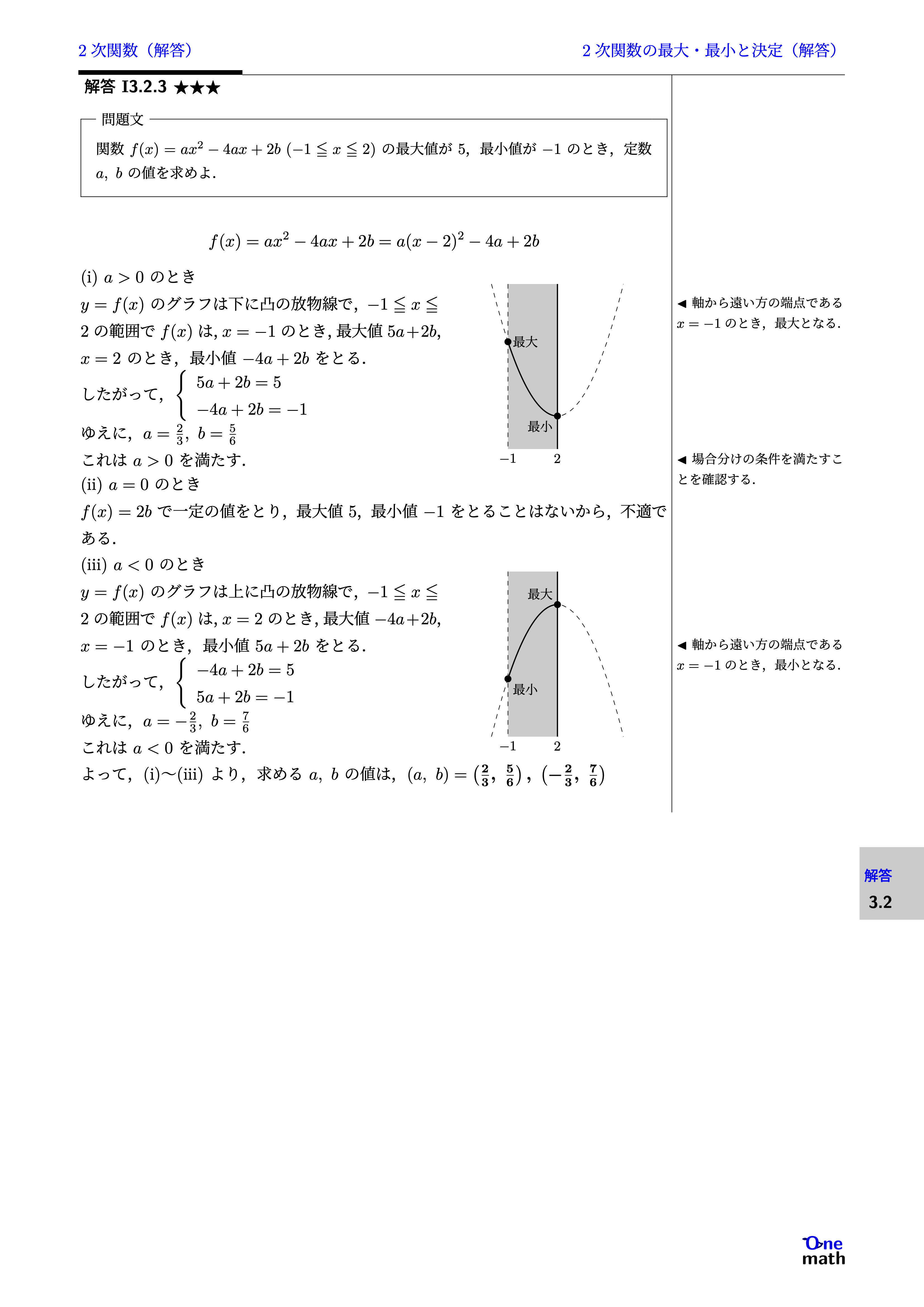
関数$f(x)=a x^2-4 a x+2b (-1 \leqq x \leqq 2)$の最大値が$5$,最小値が$-1$のとき,定数$a,b$の値を求めよ.
% 解答I3.2.3
$f(x)=a x^2-4 a x+2b=a(x-2)^2-4a+2b$(i)$a>0$のとき$y=f(x)$のグラフは下に凸の放物線で,$-1 \leqq x \leqq 2$の範囲で$f(x)$は,$x=-1$のとき,最大値$5a+2b,x=2$のとき,最小値$-4a+2b$をとる. したがって,$\left\{\begin{array}{l} 5a+2b=5 \\-4a+2b=-1 \end{array}\right.$ゆえに,$a=\frac{2}{3},b=\frac{5}{6}$これは$a>0$を満たす. (ii)$a=0$のとき$f(x)=2b$で一定の値をとり,最大値$5$,最小値$-1$をとることはないから,不適である. (iii)$a<0$のとき$y=f(x)$のグラフは上に凸の放物線で,$-1 \leqq x \leqq 2$の範囲で$f(x)$は,$x=2$のとき,最大値$-4a+2b,x=-1$のとき,最小値$5a+2b$をとる. したがって,$\left\{\begin{array}{l}-4a+2b=5 \\ 5a+2b=-1 \end{array}\right.$ゆえに,$a=-\frac{2}{3},b=\frac{7}{6}$これは$a<0$を満たす. よって,(i)〜(iii)より,求める$a,b$の値は,$(a,b)=\left(\frac{2}{3},\frac{5}{6}\right),\left(-\frac{2}{3},\frac{7}{6}\right)$
