% 例題I3.2.9：条件付きの2変数関数の最大・最小1 （One More）★★★
$2x+y=1$を満たすとき,次の問いに答えよ. (1)$x^2+y^2$の最小値を求めよ. (2)$x \geqq 0,y \geqq 0$のとき,$x^2+y^2$の最大値を求めよ.
% 解答（例題I3.2.9）
(1)$2x+y=1$より,$y=1-2x \cdots (\mathrm{i})$したがって,$$\begin{aligned} x^2+y^2 &=x^2+(1-2 x)^2\\ &=5 x^2-4x+1 \\ &=5\left(x-\frac{2}{5}\right)^2+\frac{1}{5} \cdots (\mathrm{ii}) \end{aligned}$$ゆえに,$x=\frac{2}{5}$で最小値$\frac{1}{5}$このとき,(i)より,$y=1-2 \cdot \frac{2}{5}=\frac{1}{5}$よって,$x=\frac{2}{5},y=\frac{1}{5}$のとき,最小値$\frac{1}{5}$(2)$y \geqq 0$であるから,(i)より,$1-2x \geqq 0$$x \geqq 0$との共通範囲は,$0 \leqq x \leqq\frac{1}{2} \cdots (\mathrm{iii})$(ii)より,(iii)において,$x^2+y^2$は$x=0$で最大値$1$このとき,(i)より,$y=1-2 \cdot 0=1$よって,$x=0,y=1$のとき,最大値$1$
% 問題I3.2.9
$x+3y=6$を満たすとき,次の問いに答えよ. (1)$x^2+y^2$の最小値を求めよ. (2)$x \geqq 0,y \geqq 0$のとき,$x^2+y^2$の最大値を求めよ.
% 解答I3.2.9
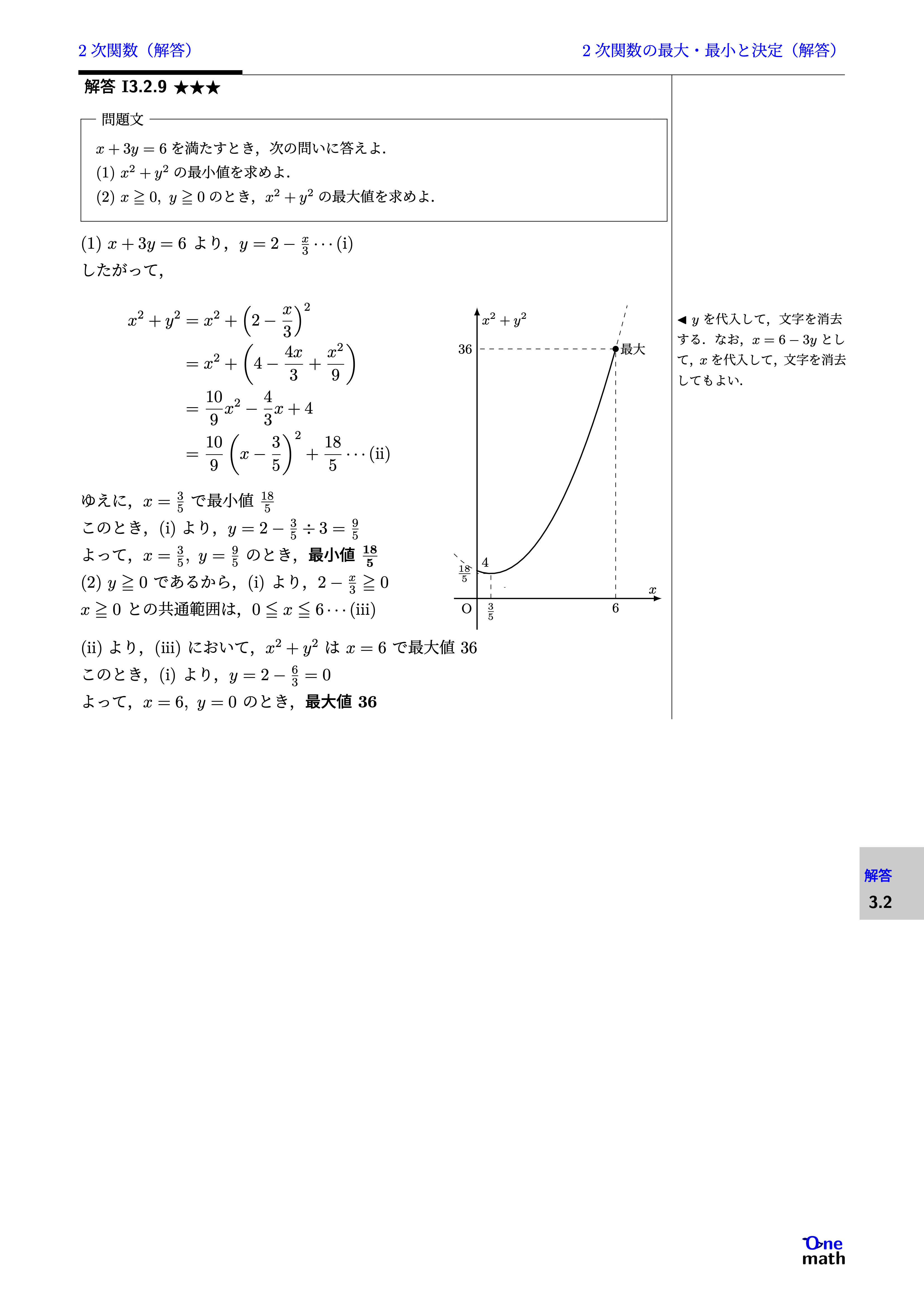
(1)$x+3y=6$より,$y=2-\frac{x}{3} \cdots (\mathrm{i})$したがって,$$\begin{aligned} x^2+y^2 &=x^2+\left(2-\frac{x}{3}\right)^2\\ &=x^2+\left(4-\frac{4x}{3}+\frac{x^2}{9}\right)\\ &=\frac{10}{9} x^2-\frac{4}{3}x+4 \\ &=\frac{10}{9}\left(x-\frac{3}{5}\right)^2+\frac{18}{5} \cdots (\mathrm{ii}) \end{aligned}$$ゆえに,$x=\frac{3}{5}$で最小値$\frac{18}{5}$このとき,(i)より,$y=2-{\frac{3}{5}}\div {3}=\frac{9}{5}$よって,$x=\frac{3}{5},y=\frac{9}{5}$のとき,最小値$\frac{18}{5}$(2)$y \geqq 0$であるから,(i)より,$2-\frac{x}{3} \geqq 0$$x \geqq 0$との共通範囲は,$0 \leqq x \leqq 6 \cdots (\mathrm{iii})$(ii)より,(iii)において,$x^2+y^2$は$x=6$で最大値$36$このとき,(i)より,$y=2-\frac{6}{3}=0$よって,$x=6,y=0$のとき,最大値$36$
