% 例題I3.2.10：2次関数の最大・最小の文章題 （One More）★★
周囲の長さが$12$である長方形において,次の問いに答えよ. (1)この長方形の面積の最大値を求めよ. (2)この長方形の対角線の長さの最小値を求めよ.
% 解答（例題I3.2.10）
(1)長方形の縦の長さを$x$とすると, 横の長さは$\frac{12-2 x}{2}=6-x$である. また,$x>0,6-x>0$であるから,$0<x<6$この長方形の面積を$y$とすると,$$y=x(6-x)=-x^2+6 x=-(x-3)^2+9$$$0<x<6$より,$y$は$x=3$で最大値9をとる. よって,長方形の面積の最大値は,$9$(2)長方形の対角線の長さを$l$とすると,$$l^2=x^2+(6-x)^2=2x^2-12x+36=2(x-3)^2+18$$$0<x<6$において,$l^2$は$x=3$で最小値$18$をとる. ここで,$l>0$であるから,$l^2$が最小となるとき,$l$も最小となる. よって,対角線の最小値は,$\sqrt{18}=3\sqrt{2}$
% 問題I3.2.10
直角を挟む2辺の長さの和が10である直角三角形において,斜辺の長さが最小となる直角三角形を求め,その斜辺の長さを求めよ.
% 解答I3.2.10
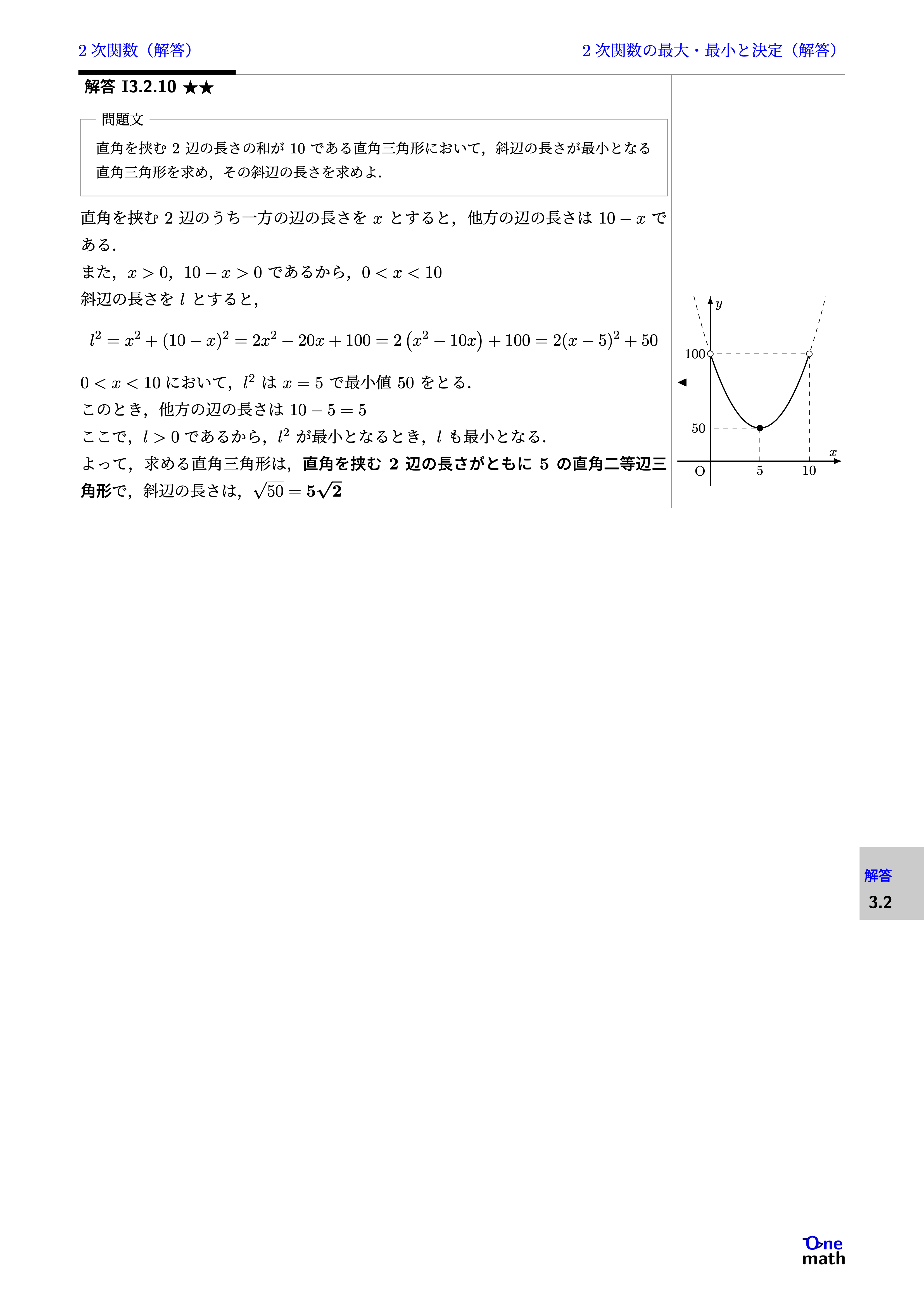
直角を挟む2辺のうち一方の辺の長さを$x$とすると,他方の辺の長さは$10-x$である. また,$x>0,10-x>0$であるから,$0<x<10$斜辺の長さを$l$とすると,$$l^2 =x^2+(10-x)^2 =2 x^2-20 x+100 =2\left(x^2-10 x\right)+100 =2(x-5)^2+50$$$0<x<10$において,$l^2$は$x=5$で最小値50をとる. このとき,他方の辺の長さは$10-5=5$ここで,$l>0$であるから,$l^2$が最小となるとき,$l$も最小となる. よって,求める直角三角形は,直角を挟む2辺の長さがともに5の直角二等辺三角形で,斜辺の長さは,$\sqrt{50}=5\sqrt{2}$
