% 節末I4.1.1★★★
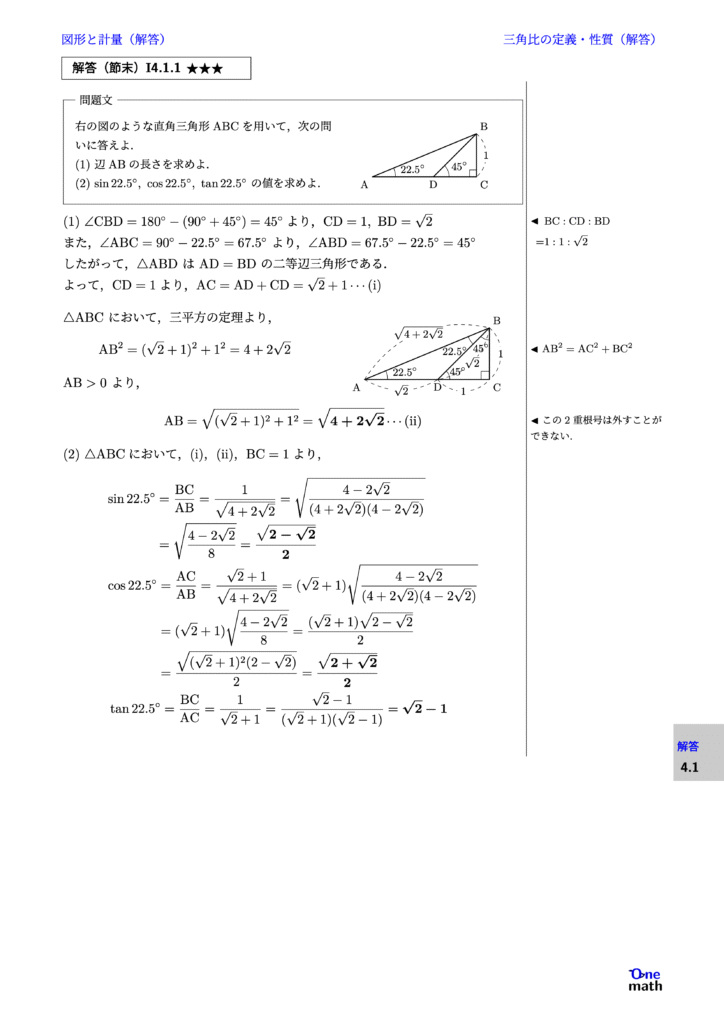
右の図のような直角三角形ABCを用いて,次の問いに答えよ. (1)辺ABの長さを求めよ. (2)$\sin 22.5^{\circ}, \cos 22.5^{\circ}, \tan 22.5^{\circ}$の値を求めよ.
% 節末I4.1.2★★★
鋭角$\theta$が$\tan \theta=\frac{5}{12}$を満たすとき,$\frac{\sin \theta}{1+\cos \theta}+\frac{\sin \theta}{1-\cos \theta}$の値を求めよ.
% 節末I4.1.3★★
$0^{\circ} \leqq \theta \leqq 180^{\circ}$において,$ \frac{1}{\sqrt{3}}\sin \theta+\cos \theta=0$を満たす$\theta$の値を求めよ.
% 節末I4.1.4★★★
$\tan \theta+\frac{1}{\tan \theta}=3$のとき,次の式の値を求めよ.ただし,$0^{\circ}<\theta<45^{\circ}$とする. (1)$\sin \theta \cos \theta$ (2)$\sin \theta+\cos \theta$ (3)$\sin \theta-\cos \theta$ (4)$\sin^3\theta-\cos^3\theta$
% 節末I4.1.5★★
2直線$\sqrt{3} x+y=0\cdots(\mathrm{i}), a x+b y+2=0\cdots(\mathrm{ii})$ がある.直線(ii)は点$(-1, \sqrt{3})$を通り,2直線(i),(ii)のなす角は$30^{\circ}$である.このとき,定数$a, b$の値を求めよ.
% 節末I4.2.1★★
$\triangle \mathrm{ABC}$の頂点$\mathrm{A}, \mathrm{B}, \mathrm{C}$の対辺をそれぞれ$a, b, c$とする.$C=60^\circ$のとき,$\frac{b}{c^2-a^2}+\frac{a}{c^2-b^2}$の値を求めよ.
% 節末I4.2.2★★★
$\triangle \mathrm{ABC}$において,$b=2, c=\sqrt{6}, B=45^{\circ}$のとき,残りの辺の長さと角の大きさを求めよ.
% 節末I4.2.3★★★
$\triangle \mathrm{ABC}$において,$(b+c):(c+a):(a+b)=4: 5: 6, R=\sqrt{3}$が成り立つとき,$\cos A, a, b, c$を求めよ.
% 節末I4.2.4★★★
$\triangle \mathrm{ABC}$において,$\mathrm{AB}=x-1, \mathrm{AC}=x, \mathrm{BC}=x+1$のとき,次の問いに答えよ. (1)$x$のとり得る値の範囲を求めよ. (2)$\triangle \mathrm{ABC}$が鈍角三角形となる$x$の値の範囲を求めよ. (3)$\triangle \mathrm{ABC}$の1つの内角が$120^\circ$であるとき,$x$の値,外接円の半径を求めよ.
% 節末I4.2.5★★★
次の等式が成り立つとき,$\triangle \mathrm{ABC}$はどのような三角形か. $$ (a-b)\sin ^2 C=a \sin ^2 A-b \sin ^2 B $$
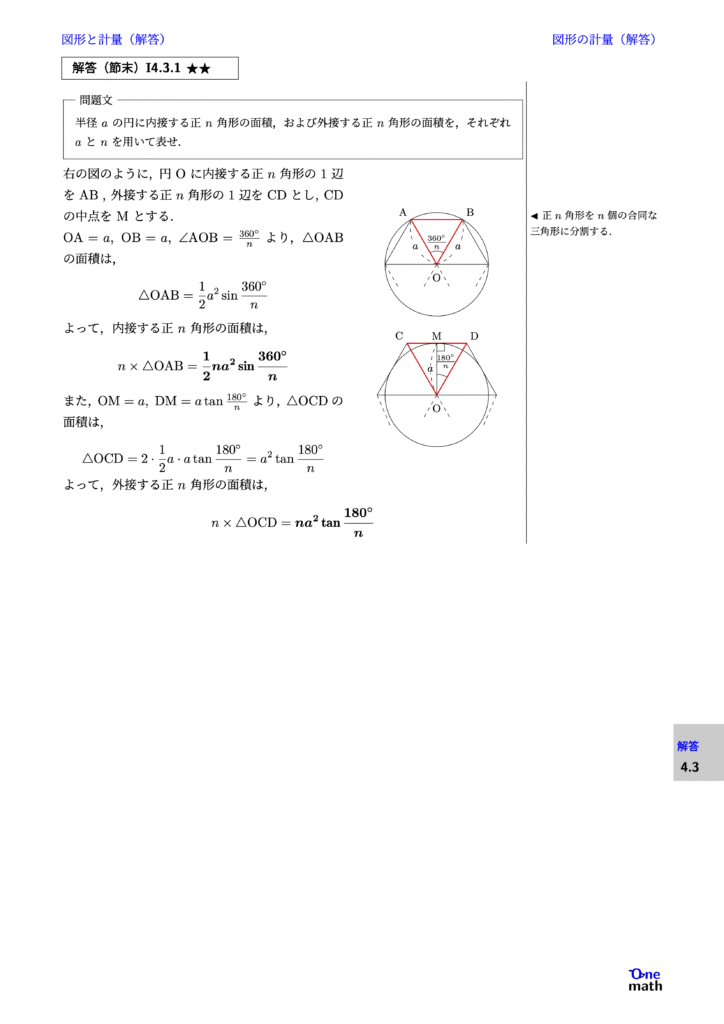
% 節末I4.3.1★★
半径$a$の円に内接する正$n$角形の面積,および外接する正$n$角形の面積を,それぞれ$a$と$n$を用いて表せ.
% 節末I4.3.2★★★
$\triangle \mathrm{ABC}$において,$\frac{\sin A}{13}=\frac{\sin B}{8}=\frac{\sin C}{7}$が成り立つとする.このとき,次の問いに答えよ. (1)$\cos A, \sin A$の値を求めよ. (2)$\triangle \mathrm{ABC}$の内接円の半径が1のとき,$\triangle \mathrm{ABC}$の面積,$\triangle \mathrm{ABC}$の外接円の半径を求めよ.
% 節末I4.3.3★★★
円に内接する四角形ABCDがある.$\mathrm{AB}=3, \mathrm{BC}=\mathrm{CD}=\sqrt{3}$,$\mathrm{DA}=2$とする.このとき,次の問いに答えよ. (1)$\cos \angle \mathrm{BAD}$と対角線BDの長さを求めよ. (2)2つの対角線ACとBDの交点をEとする.$\mathrm{BE} : \mathrm{ED}$とBEの長さを求めよ.
% 節末I4.3.4★★★
$\mathrm{AB}=\sqrt{6}, \mathrm{AD}=\sqrt{3}, \mathrm{AE}=1$である右の図のような直方体$\mathrm{ABCD}-\mathrm{EFGH}$がある.このとき,次の値を求めよ. (1)$\angle \mathrm{ACF}$ (2)$\triangle \mathrm{ACF}$の面積 (3)四面体$\mathrm{BAFC}$の体積 (4)Bから平面$\mathrm{AFC}$に下ろした垂線の長さ
% 節末I4.3.5★★★
底面の半径$\sqrt{5}$の直円錐に半径1の球が内接している.このとき,この直円錐の体積を求めよ.
% 章末I4.1★★
$\sin \theta+\cos \theta=\frac{1}{\sqrt{5}}$のとき,$\tan ^3 \theta+\frac{1}{\tan ^3 \theta}$の値を求めよ.
% 章末I4.2★★★★
$\sin ^2 \theta+2 a \cos \theta-3=0$が$90^{\circ} \leqq \theta \leqq 180^{\circ}$の範囲に解をもつための定数$a$の値の範囲を求めよ.
% 章末I4.3★★★
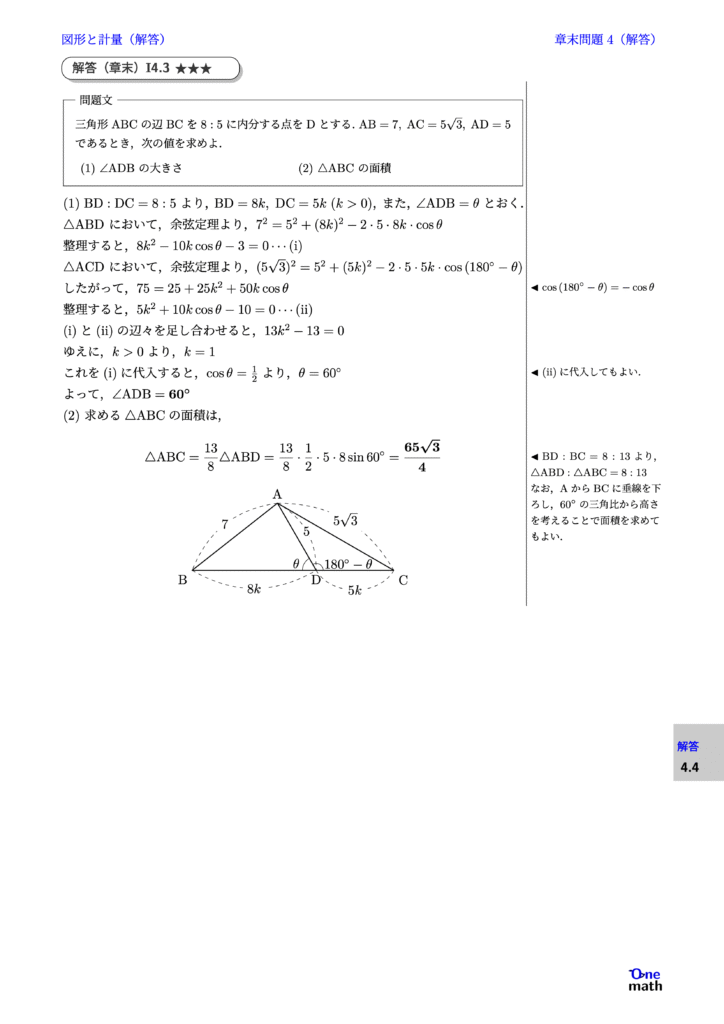
三角形ABCの辺BCを$8: 5$に内分する点をDとする.$\mathrm{AB}=7, \mathrm{AC}=5\sqrt{3}, \mathrm{AD}=5$であるとき,次の値を求めよ. (1)$\angle \mathrm{ADB}$の大きさ (2)$\triangle \mathrm{ABC}$の面積
% 章末I4.4★★★★
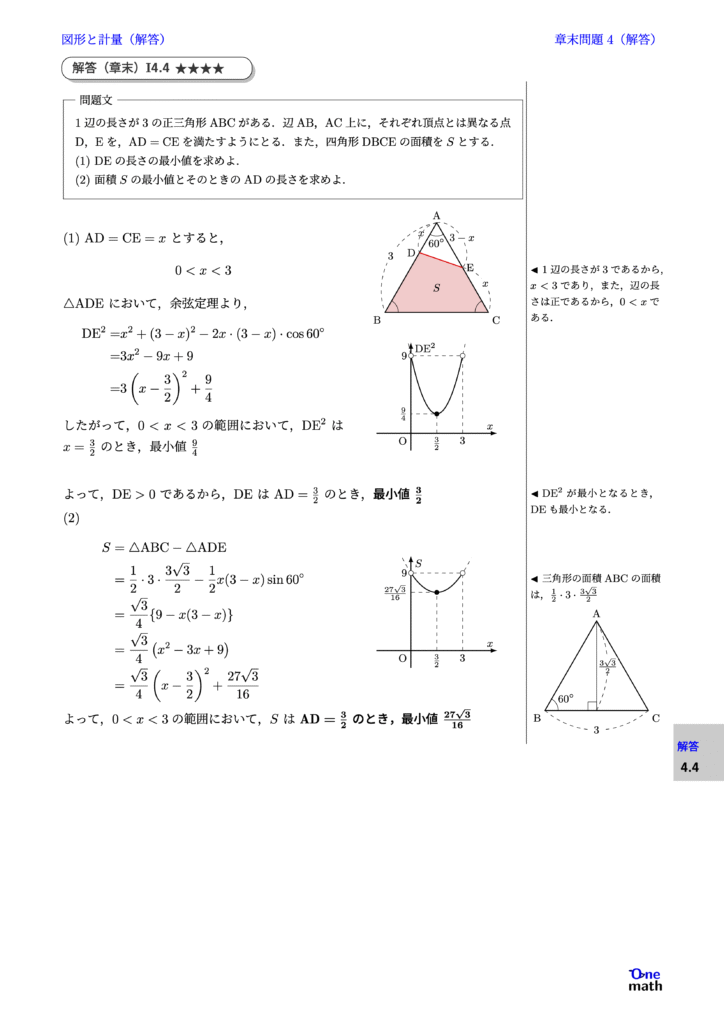
1辺の長さが3の正三角形ABCがある.辺AB,AC上に,それぞれ頂点とは異なる点D,Eを,$\mathrm{AD}=\mathrm{CE}$を満たすようにとる.また,四角形DBCEの面積を$S$とする. (1)DEの長さの最小値を求めよ. (2)面積$S$の最小値とそのときのADの長さを求めよ.
% 章末I4.5★★★
1辺の長さが6の正四面体ABCDについて,辺BC上に$\mathrm{BE}: \mathrm{EC}=1: 2$となるように点Eをとり,辺CDの中点をM,$\angle \mathrm{EAM}=\theta$とする.このとき,次の値を求めよ. (1)$\cos \theta$ (2)$\triangle \mathrm{AEM}$の面積$S$
% 解答（節末）I4.1.1
(1)$\angle \mathrm{CBD}=180^\circ-(90^\circ+45^{\circ})=45^\circ$より,$\mathrm{CD=1, \mathrm{BD}=\sqrt{2} }$ また,$\angle \mathrm{ABC}=90^{\circ}-22.5^{\circ}=67.5^{\circ}$より,$\angle \mathrm{ABD}=67.5^{\circ}-22.5^{\circ}=45^{\circ}$ したがって,$\triangle \mathrm{ABD}$は$\mathrm{AD}=\mathrm{BD}$の二等辺三角形である. よって,$\mathrm{CD}=1$より,$\mathrm{AC}=\mathrm{AD}+\mathrm{CD}=\sqrt{2}+1\cdots(\mathrm{i})$ $\triangle \mathrm{ABC}$において,三平方の定理より, $$ \mathrm{AB}^2=(\sqrt{2}+1)^2+1^2=4+2\sqrt{2} $$ $\mathrm{AB}>0$より, $$ \mathrm{AB}=\sqrt{(\sqrt{2}+1)^2+1^2}=\sqrt{4+2\sqrt{2}}\cdots(\mathrm{ii}) $$ (2)$\triangle \mathrm{ABC}$において,(i),(ii),$\mathrm{BC}=1$より, $$ \begin{aligned} &\begin{aligned} \sin 22.5^{\circ}&=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{4+2\sqrt{2}}}=\sqrt{\frac{4-2\sqrt{2}}{(4+2\sqrt{2})(4-2\sqrt{2})}}\\ &=\sqrt{\frac{4-2\sqrt{2}}{8}}=\frac{\sqrt{2-\sqrt{2}}}{2} \end{aligned} \\& \begin{aligned} \cos 22.5^{\circ}&=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{2}+1}{\sqrt{4+2\sqrt{2}}} =(\sqrt{2}+1)\sqrt{\frac{4-2\sqrt{2}}{(4+2\sqrt{2})(4-2\sqrt{2})}} \\ &=(\sqrt{2}+1)\sqrt{\frac{4-2\sqrt{2}}{8}}=\frac{(\sqrt{2}+1)\sqrt{2-\sqrt{2}}}{2} \\ &=\frac{\sqrt{(\sqrt{2}+1)^2(2-\sqrt{2})}}{2}=\frac{\sqrt{2+\sqrt{2}}}{2} \end{aligned} \\& \tan 22.5^{\circ}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{1}{\sqrt{2}+1}=\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}=\sqrt{2}-1 \end{aligned} $$
% 解答（節末）I4.1.2
$$ \begin{aligned} \frac{\sin \theta}{1+\cos \theta}+\frac{\sin \theta}{1-\cos \theta} &=\frac{\sin \theta(1-\cos \theta)+\sin \theta(1+\cos \theta)}{(1+\cos \theta)(1-\cos \theta)} \\ &=\frac{\sin \theta-\sin \theta \cos \theta+\sin \theta+\sin \theta \cos \theta}{1-\cos ^2 \theta} \\ &=\frac{2 \sin \theta}{\sin ^2 \theta}=\frac{2}{\sin \theta} \end{aligned} $$ また, $$ \cos ^2 \theta=\frac{1}{1+\tan ^2 \theta}=\frac{1}{1+\left(\frac{5}{12}\right)^2}=\frac{144}{169}, $$ $$ \sin ^2 \theta=1-\cos ^2 \theta=1-\frac{144}{169}=\frac{25}{169} $$ $\theta$は鋭角であるから,$\sin \theta>0$ したがって,$\sin \theta=\frac{5}{13}$ よって, $$ \frac{\sin \theta}{1+\cos \theta}+\frac{\sin \theta}{1-\cos \theta}=\frac{2}{\sin \theta}=2 \div \frac{5}{13}=\frac{26}{5} $$ 別解：$\tan \theta=\frac{5}{12}$より, $$ \cos ^2 \theta=\frac{1}{1+\tan ^2 \theta}=\frac{1}{1+\left(\frac{5}{12}\right)^2}=\frac{144}{169} $$ $\theta$は鋭角であるから,$\cos \theta>0$ したがって,$\cos \theta=\frac{12}{13}$ また,$\sin \theta=\cos \theta \tan \theta=\frac{12}{13} \cdot \frac{5}{12}=\frac{5}{13}$ よって,これらを代入して, $$ \frac{\sin \theta}{1+\cos \theta}+\frac{\sin \theta}{1-\cos \theta}=\frac{5}{13} \div \frac{25}{13}+\frac{5}{13} \div \frac{1}{13}=\frac{26}{5} $$
% 解答（節末）I4.1.3
$\cos \theta=0$のとき,$\theta=90^{\circ}$であり,これは方程式を満たさない. したがって,$\cos \theta \neq 0$ $\frac{1}{\sqrt{3}}\sin \theta+\cos \theta=0$より,$\sin \theta=-\sqrt{3}\cos \theta$ 両辺を$\cos \theta$で割ると,$\frac{\sin \theta}{\cos \theta}=-{\sqrt{3}}$ よって,$\tan \theta=-{\sqrt{3}}$ $0^{\circ} \leqq \theta \leqq 180^{\circ}$であるから,$\theta=120^{\circ}$
% 解答（節末）I4.1.4
(1) $$ \tan \theta+\frac{1}{\tan \theta}=\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta}=\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin \theta \cos \theta} =\frac{1}{\sin \theta \cos \theta} $$ $\tan \theta+\frac{1}{\tan \theta}=3$であるから,$\frac{1}{\sin \theta \cos \theta}=3$ よって,$\sin \theta \cos \theta=\frac{1}{3}\cdots(\mathrm{i})$ (2) $$ (\sin \theta+\cos \theta)^2=\sin ^2 \theta+2 \sin \theta \cos \theta+\cos ^2 \theta=1+2 \sin \theta \cos \theta $$ (i)より,$(\sin \theta+\cos \theta)^2=1+2 \cdot \frac{1}{3}=\frac{5}{3} $ $0^{\circ}<\theta<45^{\circ}$のとき,$\sin \theta>0, \cos \theta>0$より, $\sin \theta+\cos \theta>0$ よって,$\sin \theta+\cos \theta=\sqrt{\frac{5}{3}}=\frac{\sqrt{15}}{3}$ (3) $$ (\sin \theta-\cos \theta)^2=\sin ^2 \theta-2 \sin \theta \cos \theta+\cos ^2 \theta =1-2 \sin \theta \cos \theta $$ (i)より,$(\sin \theta-\cos \theta)^2=1-2 \cdot \frac{1}{3}=\frac{1}{3} $ $0^{\circ}<\theta<45^{\circ}$のとき,$\sin \theta<\cos \theta$より, $ \sin \theta-\cos \theta<0 $ よって,$\sin \theta-\cos \theta=-\sqrt{\frac{1}{3}}=-\frac{\sqrt{3}}{3}$ (4) $\begin{aligned} \sin ^3 \theta-\cos ^3 \theta &=(\sin \theta-\cos \theta)\left(\sin ^2 \theta+\sin \theta \cos \theta+\cos ^2 \theta\right)\\ &=-\frac{\sqrt{3}}{3} \cdot\left(1+\frac{1}{3}\right)=-\frac{4 \sqrt{3}}{9}\end{aligned}$
% 解答（節末）I4.1.5
$\sqrt{3} x+y=0$より,$y=-\sqrt{3} x$ 直線(i)が$x$軸の正の向きとのなす角を$\theta$とすると, $ \tan \theta=-\sqrt{3} $ $0^{\circ} \leqq \theta<180^{\circ}$より,$\theta=120^{\circ}$ 2直線(i),(ii)のなす角が$30^{\circ}$であるから,直線(ii)が$x$軸の正の向きとのなす角は$90^{\circ}$または$150^{\circ}$ （ア）$90^{\circ}$のとき 直線(ii)は点$(-1, \sqrt{3})$を通り,$y$軸に平行であるから, $ x=-1 $ 式変形すると,$2x+2=0$ したがって,これと(ii)を比較すると, $ a=2, b=0 $ （イ）$150^{\circ}$のとき $\tan 150^{\circ}=-\frac{1}{\sqrt{3}}$より,直線(ii)の傾きは$-\frac{1}{\sqrt{3}}$ 直線(ii)は点$(-1, \sqrt{3})$を通るから, $ y=-\frac{1}{\sqrt{3}}(x+1)+\sqrt{3} $ 式変形すると,$-x-\sqrt{3} y+2=0$ したがって,これと(ii)を比較すると, $a=-1, b=-\sqrt{3}$ よって,（ア）,（イ）より, $ a=2 , b=0 $ または$ a=-1 , b=-\sqrt{3}$
% 解答（節末）I4.2.1
余弦定理より, $c^2=a^2+b^2-2 ab \cos 60^{\circ}=a^2+b^2-2 ab \cdot \frac{1}{2}=a^2+b^2-ab$ 整理すると,$c^2-a^2=b^2-ab$ また,$c^2-b^2=a^2-ab$ よって,これらを与えられた式に代入すると, $$\begin{aligned} \frac{b}{c^2-a^2}+\frac{a}{c^2-b^2}&=\frac{b}{b^2-ab}+\frac{a}{a^2-ab}\\ &=\frac{b}{b(b-a)}+\frac{a}{a(a-b)}\\ &=\frac{1}{b-a}+\frac{1}{a-b}=0\end{aligned}$$
% 解答（節末）I4.2.2
正弦定理より,$\frac{2}{\sin 45^{\circ}}=\frac{\sqrt{6}}{\sin C}$ したがって, $ \sin C=\sqrt{6} \cdot \frac{\sin 45^{\circ}}{2}=\frac{\sqrt{3}}{2} $ $B=45^{\circ}$より,$0^{\circ}<C<135^{\circ}$であるから, $$C=60^{\circ}, 120^{\circ}$$ (i)$C=60^{\circ}$のとき $$ A=180^{\circ}-(B+C)=75^{\circ} $$ 余弦定理より, $ 2^2=a^2+(\sqrt{6})^2-2 \cdot a \cdot \sqrt{6} \cdot \cos 45^{\circ} $ したがって, $ a^2-2\sqrt{3} a+2=0 $より,$a=\sqrt{3} \pm 1$ ここで,$A$が最大の角であるから,対辺$a$が最大の辺である. ゆえに,$a>\sqrt{6}$より,$a=\sqrt{3}+1$ (ii)$C=120^{\circ}$のとき $$ A=180^{\circ}-(B+C)=15^{\circ} $$ 余弦定理より, $ 2^2=a^2+(\sqrt{6})^2-2 \cdot a \cdot \sqrt{6} \cdot \cos 45^{\circ} $ したがって, $ a^2-2\sqrt{3}a+2=0 $より,$a=\sqrt{3}\pm 1$ ここで,$A$が最小の角であるから,対辺$a$が最小の辺である. ゆえに,$a<2$より,$a=\sqrt{3}-1$ よって,(i),(ii)より, $$ A=75^{\circ}, C=60^{\circ}, a=\sqrt{3}+1 \text{ または } A=15^{\circ}, C=120^{\circ}, a=\sqrt{3}-1 $$
% 解答（節末）I4.2.3
$(b+c):(c+a):(a+b)=4: 5: 6$であるから, $ b+c=8 k, c+a=10 k, a+b=12 k(k>0)\cdots(\mathrm{i}) $ とおくと,これらの辺々を足し合わせると, $ 2(a+b+c)=30 k $ したがって, $ a+b+c=15 k\cdots(\mathrm{ii}) $ (i),(ii)より,$a=7 k, b=5 k, c=3 k\cdots(\mathrm{iii})$ 余弦定理より,$\cos A=\frac{(5 k)^2+(3 k)^2-(7 k)^2}{2 \cdot 5 k \cdot 3 k}=-\frac{1}{2}$ $\cos A=-\frac{1}{2}$であるから,$A=120^\circ$ これと$R=\sqrt{3}$であるから,正弦定理より, $\frac{a}{\sin120^\circ}=2\sqrt{3}$ よって,$a=2\sqrt{3}\sin120^\circ=3$ このとき,(iii)より,$k=\frac{3}{7}$であり,$b=\frac{15}{7}, c=\frac{9}{7}$
% 解答（節末）I4.2.4
(1) $x-1<x<x+1$であるから,三角形が成立する条件より,$$x+1<x+(x-1)$$ よって,$x$のとり得る値の範囲は,$x>2\cdots(\mathrm{i})$ (2)辺$\mathrm{BC}$が最大の辺であるから,鈍角三角形となる条件は$A>90^{\circ}$,すなわち,$\cos A<0$である. 余弦定理より, $$ \cos A=\frac{ x^2+(x-1)^2-(x+1)^2}{2x(x-1)}<0 $$ したがって,$x^2+(x-1)^2-(x+1)^2<0$ 整理すると,$x^2-4x<0$ ゆえに,$x(x-4)<0$ これを解くと,$0<x<4 \cdots(\mathrm{ii})$ よって,(i),(ii)より,求める$x$の値の範囲は,$2<x<4$$\cdots(\mathrm{iii})$ (3)長さ$x+1$の辺に対する角が$120^{\circ}$になるから,余弦定理より, $$ (x+1)^2=x^2+(x-1)^2-2\cdot x\cdot(x-1)\cdot \cos 120^{\circ} $$ したがって,$2x^2-5x=0$であるから,$x(2x-5)=0$ (iii)より,$2<x<4$であるから$x=\frac{5}{2}$ 外接円の半径を$R$とすると,正弦定理より, $\frac{x+1}{\sin 120^{\circ}}=2 R$ よって,$R=\frac{1}{2}\cdot\frac{\frac{5}{2}+1}{\sin 120^\circ}=\frac{1}{2}\cdot\frac{7}{2}\div \frac{\sqrt{3}}{2}=\frac{7}{2\sqrt{3}}=\frac{7\sqrt{3}}{6}$
% 解答（節末）I4.2.5
正弦定理より, $$ (a-b)\left(\frac{c}{2 R}\right)^2=a\left(\frac{a}{2 R}\right)^2-b\left(\frac{b}{2 R}\right)^2 $$ 両辺に$4 R^2$を掛けると, $$ (a-b)c^2=a^3-b^3 $$ したがって, $ (a-b)c^2=(a-b)\left(a^2+ab+b^2\right) $ ゆえに, $ (a-b)\left\{c^2-\left(a^2+ab+b^2\right)\right\}=0 $ したがって,$a=b$または$c^2-\left(a^2+ab+b^2\right)=0$ (i)$a=b$のとき $\triangle \mathrm{ABC}$は$\mathrm{BC}=\mathrm{CA}$の二等辺三角形である. (ii)$c^2=a^2+ab+b^2$のとき 余弦定理より, $$ \cos C=\frac{a^2+b^2-c^2}{2 ab}=\frac{a^2+b^2-\left(a^2+ab+b^2\right)}{2ab}=\frac{-ab}{2ab}=-\frac{1}{2} $$ したがって,$C=120^{\circ}$ よって,(i),(ii)より,$\triangle \mathrm{ABC}$は $\mathrm{BC}=\mathrm{CA}$の二等辺三角形または$C=120^{\circ}$の三角形
% 解答（節末）I4.3.1
右の図のように,円Oに内接する正$n$角形の1辺をAB,外接する正$n$角形の1辺をCDとし,CDの中点をMとする. $\mathrm{OA}=a, \mathrm{OB}=a, \angle \mathrm{AOB}=\frac{360^{\circ}}{n}$より,$\triangle \mathrm{OAB}$の面積は, $$ \triangle \mathrm{OAB}=\frac{1}{2} a^2 \sin \frac{360^{\circ}}{n} $$ よって,内接する正$n$角形の面積は, $$n \times \triangle \mathrm{OAB}=\frac{1}{2} n a^2 \sin \frac{360^{\circ}}{n}$$ また, $\mathrm{OM}=a, \mathrm{DM}=a \tan \frac{180^{\circ}}{n}$より,$\triangle \mathrm{OCD}$の面積は, $$ \triangle \mathrm{OCD}=2 \cdot \frac{1}{2} a \cdot a \tan \frac{180^{\circ}}{n} =a^2 \tan \frac{180^{\circ}}{n} $$ よって,外接する正$n$角形の面積は, $$ n \times \triangle \mathrm{OCD}=n a^2 \tan \frac{180^{\circ}}{n} $$
% 解答（節末）I4.3.2
(1)正弦定理$\frac{\mathrm{BC}}{\sin A}=\frac{\mathrm{CA}}{\sin B}=\frac{\mathrm{AB}}{\sin C}$より, $$ \mathrm{BC}: \mathrm{CA}: \mathrm{AB}=\sin A: \sin B: \sin C\cdots(\mathrm{i}) $$ $\frac{\sin A}{13}=\frac{\sin B}{8}=\frac{\sin C}{7}$より, $$ \sin A: \sin B: \sin C=13: 8: 7\cdots(\mathrm{ii}) $$ (i),(ii)より,$\mathrm{BC}: \mathrm{CA}: \mathrm{AB}=13: 8: 7$ $\mathrm{BC}=13 k, \mathrm{CA}=8 k, \mathrm{AB}=7 k(k>0)$とおくと, 余弦定理より, $$ \cos A=\frac{(8 k)^2+(7 k)^2-(13 k)^2}{2 \cdot 8 k \cdot 7 k}=-\frac{1}{2} $$ $0^{\circ}<A<180^{\circ}$であるから,$\sin A>0$より, $$ \sin A=\sqrt{1-\cos ^2 A}=\sqrt{1-\left(-\frac{1}{2}\right)^2}=\frac{\sqrt{3}}{2} $$ (2)$\triangle \mathrm{ABC}$の面積を$S$とする. $$ S=\frac{1}{2} \cdot 8 k \cdot 7 k \cdot \sin A=14\sqrt{3}k^2 $$ また,内接円の半径が1であるから, $$ S=\frac{1}{2}\cdot(13 k+8 k+7 k)\cdot 1=14k $$ したがって,$ 7k(\sqrt{3} k-1)=0 $ $k>0$より,$k=\frac{1}{\sqrt{3}}$ ゆえに,$\mathrm{AB}=7 k=7\cdot \frac{1}{\sqrt{3}}=\frac{7\sqrt{3}}{3}$ 求める$\triangle \mathrm{ABC}$の面積$S$は,$S=14k=14\cdot \frac{1}{\sqrt{3}}=\frac{14\sqrt{3}}{3}$ 外接円の半径を$R$とすると,正弦定理より, $ \frac{13 k}{\sin A}=2 R $ よって,$\triangle \mathrm{ABC}$の外接円の半径は, $$ R=\frac{13 k}{2 \sin A}=13 \cdot \frac{1}{\sqrt{3}} \div \left(2\cdot \frac{\sqrt{3}}{2}\right)=\frac{13}{3} $$
% 解答（節末）I4.3.3
(1)四角形ABCDは円に内接するから, $$\angle{\mathrm{BCD}}=180^\circ-\angle\mathrm{BAD} $$ $\triangle \mathrm{ABD}$において,余弦定理より, $$ \mathrm{BD}^2=3^2+2^2-2 \cdot 3 \cdot 2 \cdot \cos \angle\mathrm{BAD} =13-12 \cos \angle\mathrm{BAD} \cdots(\mathrm{i}) $$ $\triangle \mathrm{BCD}$において,余弦定理より, $$ \mathrm{BD}^2=(\sqrt{3})^2+(\sqrt{3})^2-2 \cdot \sqrt{3} \cdot \sqrt{3} \cdot \cos \left(180^{\circ}-\angle\mathrm{BAD}\right) =6+6 \cos \angle\mathrm{BAD} \cdots(\mathrm{ii}) $$ (i),(ii)より, $ 13-12 \cos \angle\mathrm{BAD}=6+6 \cos \angle\mathrm{BAD} $ したがって,$\cos \angle\mathrm{BAD}=\frac{7}{18}$ (i)に代入すると,$\mathrm{BD}^2=13-12\cdot \left(\frac{7}{18}\right)=\frac{25}{3}$ よって,$\mathrm{BD}>0$より,$\mathrm{BD}=\frac{5}{\sqrt{3}}=\frac{5\sqrt{3}}{3}$ (2)$\mathrm{BE}: \mathrm{ED}=\triangle \mathrm{ABC}: \triangle \mathrm{ACD}=\mathrm{AB} \cdot \mathrm{BC}: \mathrm{CD} \cdot \mathrm{DA} =3 \cdot \sqrt{3}: \sqrt{3} \cdot 2=3: 2 $ よって,$\mathrm{BE}=\mathrm{BD} \cdot \frac{3}{3+2}=\frac{5\sqrt{3}}{3} \cdot \frac{3}{5}=\sqrt{3}$
% 解答（節末）I4.3.4
(1)$\mathrm{AC}^2=\mathrm{AB}^2+\mathrm{BC}^2$より,$\mathrm{AC}=\sqrt{6+3}=\sqrt{9}=3$ $\mathrm{AF}^2=\mathrm{AE}^2+\mathrm{EF}^2$より, $\mathrm{AF}=\sqrt{6+1}=\sqrt{7}$ $\mathrm{CF}^2=\mathrm{BF}^2+\mathrm{BC}^2$より, $\mathrm{CF}=\sqrt{1+3}=\sqrt{4}=2$ $\triangle \mathrm{AFC}$において,余弦定理より, $$ \cos \angle \mathrm{ACF}=\frac{3^2+2^2-(\sqrt{7})^2}{2 \cdot 3 \cdot 2}=\frac{1}{2} $$ よって,$0^{\circ}<\angle \mathrm{ACF}<180^{\circ}$より,$\angle \mathrm{ACF}=60^\circ$ (2)$\triangle \mathrm{ACF}$の面積を$S$とすると, $ S=\frac{1}{2} \cdot 3 \cdot 2 \cdot \sin \angle \mathrm{ACF}=\frac{1}{2}\cdot 3\cdot 2 \cdot \frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2} $ (3)四面体$\mathrm{BAFC}$の体積を$V$とすると, $$ V=\frac{1}{3} \cdot \triangle \mathrm{ABF} \cdot \mathrm{BC} =\frac{1}{3} \cdot\left(\frac{1}{2} \cdot \sqrt{6} \cdot 1\right)\cdot \sqrt{3}=\frac{\sqrt{18}}{6}=\frac{\sqrt{2}}{2}\cdots(\mathrm{i}) $$ (4)求める垂線の長さを$h$とすると,$V=\frac{1}{3} \cdot \triangle \mathrm{ACF} \cdot h$ したがって,(i),(ii)より,$\frac{\sqrt{2}}{2}=\frac{1}{3} \cdot \frac{3\sqrt{3}}{2} \cdot h \cdots(\mathrm{ii})$ よって, $ h=\frac{\sqrt{6}}{3} $
% 解答（節末）I4.3.5
右の図のように,直円錐の頂点Aと底面の円の直径BCを含む平面(切断面)を考える. 球の中心をO,直円錐と球との接点を$\mathrm{D}, \mathrm{E}, \mathrm{F}$とし, $\mathrm{AD}=x, \mathrm{AO}=y$とおく. $\triangle \mathrm{ADO} \sim \triangle \mathrm{AEB}$より, $\mathrm{AD}: \mathrm{AE}=\mathrm{DO}: \mathrm{EB}$,すなわち,$x:(y+1)=1: \sqrt{5} \cdots(\mathrm{i})$ $\mathrm{AO}: \mathrm{AB}=\mathrm{DO}: \mathrm{EB}$,すなわち,$y:(x+\sqrt{5})=1: \sqrt{5}\cdots(\mathrm{ii})$ (i)より,$y+1=\sqrt{5} x\cdots(\mathrm{iii})$ (ii)より,$x+\sqrt{5}=\sqrt{5} y$,すなわち,$x=\sqrt{5}(y-1)\cdots(\mathrm{iv})$ (iii),(iv)より, $ y+1=\sqrt{5} \cdot \sqrt{5}(y-1) $ したがって,$y+1=5(y-1)$より,$y=\frac{3}{2}$ このとき,これを(iv)に代入すると,$x=\frac{\sqrt{5}}{2}$ よって,求める直円錐の体積を$V$とすると, $ V=\frac{1}{3} \cdot \pi \cdot(\sqrt{5})^2 \cdot\left(\frac{3}{2}+1\right)=\frac{25}{6}\pi $
% 解答（章末）I4.1
$$ \begin{aligned} \tan ^3 \theta+\frac{1}{\tan ^3 \theta} =& \left(\tan \theta+\frac{1}{\tan \theta}\right)^3-3 \tan \theta \cdot \frac{1}{\tan \theta}\left(\tan \theta+\frac{1}{\tan \theta}\right)\\ =& \left(\tan \theta+\frac{1}{\tan \theta}\right)^3-3\left(\tan \theta+\frac{1}{\tan \theta}\right)\cdots(\mathrm{i}) \end{aligned} $$ また, $$ \tan \theta+\frac{1}{\tan \theta}=\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta}=\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin \theta \cos \theta}=\frac{1}{\sin \theta \cos \theta}\cdots(\mathrm{ii}) $$ $\sin \theta+\cos \theta=\frac{1}{\sqrt{5}}$の両辺を2乗すると, $ \sin ^2 \theta+2 \sin \theta \cos \theta+\cos ^2 \theta=\frac{1}{5} $ したがって,$1+2 \sin \theta \cos \theta=\frac{1}{5}$ 整理すると,$\sin \theta \cos \theta=-\frac{2}{5}$ ゆえに,(ii)より, $ \tan \theta+\frac{1}{\tan \theta}=-\frac{5}{2} $ よって,(i)より, $ \tan ^3 \theta+\frac{1}{\tan ^3 \theta}=\left(-\frac{5}{2}\right)^3-3 \cdot\left(-\frac{5}{2}\right)=-\frac{65}{8} $
% 解答（章末）I4.2
$\cos \theta=t$とおくと,与えられた方程式は, $ 1-t^2+2 a t-3=0 $,すなわち,$ t^2-2 a t+2=0 $となり,この2次方程式の判別式を$D$とする. $90^{\circ} \leqq \theta \leqq 180^{\circ}$のとき,$-1 \leqq \cos \theta \leqq 0$より,$-1 \leqq t \leqq 0$ $ f(t)=t^2-2 a t+2 $とおくと,与えられた方程式が$90^{\circ} \leqq \theta \leqq 180^{\circ}$に解をもつのは,$y=f(t)$のグラフが$-1 \leqq t \leqq 0$の範囲で$t$軸と共有点をもつときである. また,$f(-1)=2 a+3, f(0)=2$より, $f(0)>0$であるから,求める条件は,(i),(ii)の場合に分けられる. (i)$f(-1) \leqq 0$,すなわち,$a \leqq -\frac{3}{2}$のとき $f(-1)\cdot f(0) \leqq 0$となることから,これは求める条件を満たす. (ii)$f(-1)>0$,すなわち,$a>-\frac{3}{2}$のとき 求める条件は,（ア）$D \geqq 0$ （イ）軸$t=a$が$-1<t<0$である. （ア）$\frac{D}{4}=(-a)^2-1\cdot 1\cdot 2=a^2-2$であり,$D \geqq 0$から, $a \leqq -\sqrt{2}, \sqrt{2} \leqq a$ （イ）$y=f(t)$の軸は直線$t=a$であり,軸が$-1<t<0$の間にあるから,$-1<a<0$ したがって,（ア）,（イ）より,これらを同時に満たす$a$の値は存在しない. よって,(i),(ii)より,求める定数$a$の値の範囲は, $ a \leqq -\frac{3}{2} $
% 解答（章末）I4.3
(1)$\mathrm{BD}: \mathrm{DC}=8: 5$より, $ \mathrm{BD}=8 k, \mathrm{DC}=5 k(k>0) $,また, $\angle \mathrm{A D B}=\theta$とおく. $\triangle \mathrm{ABD}$において,余弦定理より, $ 7^2=5^2+(8 k)^2-2 \cdot 5 \cdot 8 k\cdot \cos \theta $ 整理すると,$8k^2-10 k \cos \theta-3=0 \cdots(\mathrm{i})$ $\triangle \mathrm{ACD}$において,余弦定理より, $ ({5\sqrt{3}})^2=5^2+(5 k)^2-2 \cdot 5 \cdot 5k\cdot \cos \left(180^{\circ}-\theta\right) $ したがって,$75=25+25k^2+50 k \cos \theta$ 整理すると,$5k^2+10k \cos \theta-10=0 \cdots(\mathrm{ii})$ (i)と(ii)の辺々を足し合わせると,$13k^2-13=0$ ゆえに,$k>0$より,$k=1$ これを(i)に代入すると,$\cos\theta=\frac{1}{2}$より,$\theta=60^\circ$ よって,$\angle \mathrm{ADB}=60^\circ$ (2)求める$\triangle \mathrm{ABC}$の面積は, $$\triangle \mathrm{ABC}=\frac{13}{8} \triangle \mathrm{ABD}=\frac{13}{8} \cdot \frac{1}{2} \cdot 5 \cdot 8 \sin 60^{\circ}=\frac{65 \sqrt{3}}{4}$$
% 解答（章末）I4.4
(1)$\mathrm{AD}=\mathrm{CE}=x$とすると, $$0<x<3$$ $\triangle \mathrm{ADE}$において,余弦定理より, $$ \begin{aligned} \mathrm{DE}^2=& x^2+(3-x)^2-2 x\cdot(3-x)\cdot \cos 60^{\circ} \\ =& 3x^2-9x+9 \\ =& 3\left(x-\frac{3}{2}\right)^2+\frac{9}{4} \end{aligned} $$ したがって,$0<x<3$の範囲において,$\mathrm{DE}^2$は$x=\frac{3}{2}$のとき,最小値$\frac{9}{4}$ よって,$\mathrm{DE}>0$であるから,DEは$\mathrm{AD}=\frac{3}{2}$のとき,最小値$\frac{3}{2}$ (2) $$ \begin{aligned} S &=\triangle \mathrm{ABC}-\triangle \mathrm{ADE} \\ &=\frac{1}{2}\cdot 3\cdot \frac{3\sqrt{3}}{2}-\frac{1}{2} x(3-x)\sin 60^{\circ}\\ &=\frac{\sqrt{3}}{4}\{9-x(3-x)\} \\ &=\frac{\sqrt{3}}{4}\left(x^2-3 x+9\right)\\ &=\frac{\sqrt{3}}{4}\left(x-\frac{3}{2}\right)^2+\frac{27\sqrt{3}}{16} \end{aligned} $$ よって,$0<x<3$の範囲において,$S$は$\mathrm{AD}=\frac{3}{2}$のとき,最小値$\frac{27\sqrt{3}}{16}$
% 解答（章末）I4.5
(1)$\triangle \mathrm{ACM}$は,$\angle \mathrm{AMC}=90^{\circ}$の直角三角形であるから,$$\mathrm{AM}=\mathrm{AC} \sin \angle \mathrm{ACM}=\mathrm{AC} \sin 60^{\circ}=6 \cdot \frac{\sqrt{3}}{2}={3\sqrt{3}}$$ $\triangle \mathrm{ABE}$において,余弦定理により, $$ \mathrm{AE}^2=6^2+2^2-2 \cdot 6 \cdot 2 \cdot \cos 60^{\circ}=28 $$ したがって,$\mathrm{AE}>0$より,$\mathrm{AE}=2\sqrt{7}$ $\triangle \mathrm{CEM}$において,余弦定理より, $$ \begin{aligned} \mathrm{EM}^2 &=\mathrm{CE}^2+\mathrm{CM}^2-2 \cdot \mathrm{CE} \cdot \mathrm{CM} \cdot \cos \angle \mathrm{ECM} \\ &=4^2+3^2-2 \cdot 4 \cdot 3 \cdot \cos 60^{\circ}=13 \end{aligned} $$ ゆえに,$\mathrm{EM}>0$より,$\mathrm{EM}=\sqrt{13}$ $\triangle{\mathrm{EAM}}$において,余弦定理より, $$ \cos \theta=\frac{(3 \sqrt{3})^2+(2 \sqrt{7})^2-(\sqrt{13})^2}{2 \cdot 3 \sqrt{3} \cdot 2 \sqrt{7}}=\frac{\sqrt{21}}{6}$$ (2)$\sin\theta>0$であるから, $$ \sin \theta=\sqrt{1-\cos^2 \theta}=\sqrt{1-\left(\frac{\sqrt{21}}{6}\right)^2}=\frac{\sqrt{15}}{6} $$ よって,求める$\triangle \mathrm{AEM}$の面積$S$は, $$ S=\frac{1}{2} \cdot \mathrm{AM} \cdot \mathrm{AE} \cdot \sin \theta=\frac{1}{2} \cdot 3 \sqrt{3} \cdot 2 \sqrt{7}\cdot \frac{\sqrt{15}}{6}=\frac{3 \sqrt{35}}{2} $$
