% 例題I3.3.24：2次不等式が整数解をもつ条件 （One More）★★★
$x$についての不等式$x^2-(a+1)x+a<0,x^2+x-6>0$を満たす整数$x$がちょうど3個存在するような定数$a$の値の範囲を求めよ.
% 解答（例題I3.3.24）
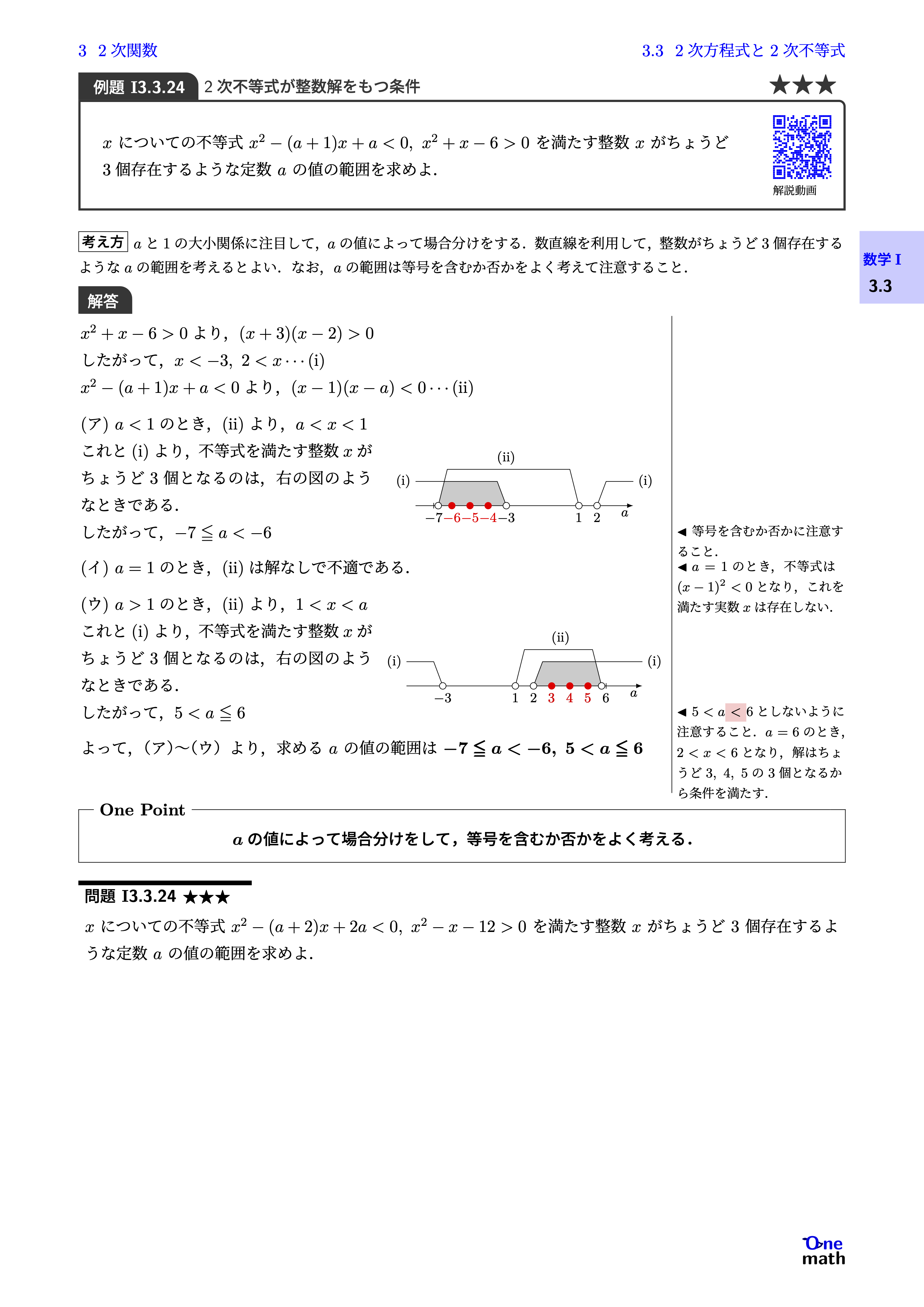
$x^2+x-6>0$より,$(x+3)(x-2)>0$したがって,$x<-3,2<x \cdots (\mathrm{i})$$x^2-(a+1)x+a<0$より,$(x-1)(x-a)<0 \cdots (\mathrm{ii})$(ア)$a<1$のとき,(ii)より,$a<x<1$これと(i)より,不等式を満たす整数$x$がちょうど3個となるのは,右の図のようなときである. したがって,$-7 \leqq a<-6$(イ)$a=1$のとき,(ii)は解なしで不適である. (ウ)$a>1$のとき,(ii)より,$1<x<a$これと(i)より,不等式を満たす整数$x$がちょうど3個となるのは,右の図のようなときである. したがって,$5<a \leqq 6$よって,（ア）〜（ウ）より,求める$a$の値の範囲は$-7 \leqq a<-6,5<a \leqq 6$
% 問題I3.3.24
$x$についての不等式$x^2-(a+2)x+2a<0,x^2-x-12>0$を満たす整数$x$がちょうど3個存在するような定数$a$の値の範囲を求めよ.
% 解答I3.3.24
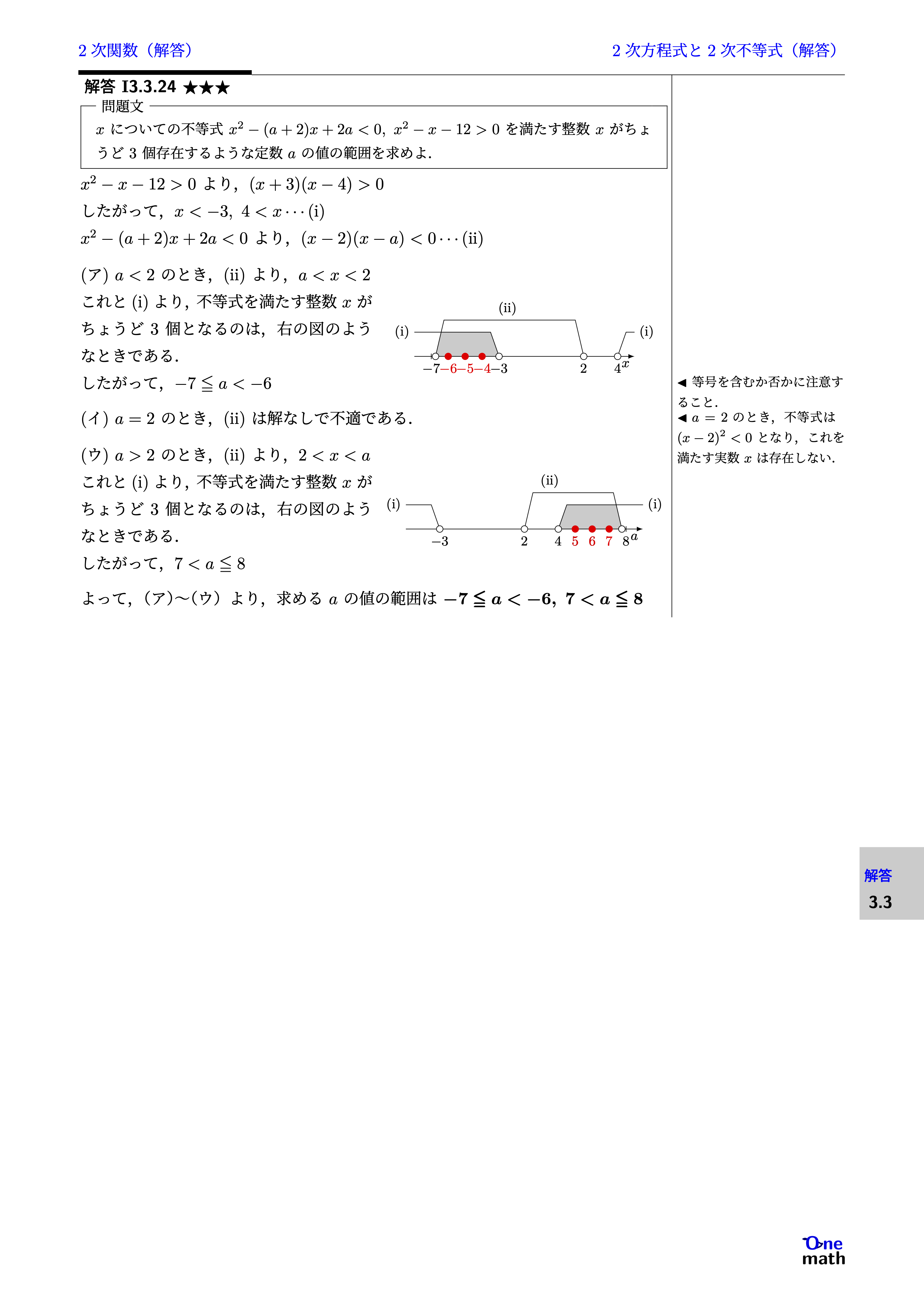
$x^2-x-12>0$より,$(x+3)(x-4)>0$したがって,$x<-3,4<x \cdots (\mathrm{i})$$x^2-(a+2)x+2a<0$より,$(x-2)(x-a)<0 \cdots (\mathrm{ii})$(ア)$a<2$のとき,(ii)より,$a<x<2$これと(i)より,不等式を満たす整数$x$がちょうど3個となるのは,右の図のようなときである. したがって,$-7 \leqq a<-6$(イ)$a=2$のとき,(ii)は解なしで不適である. (ウ)$a>2$のとき,(ii)より,$2<x<a$これと(i)より,不等式を満たす整数$x$がちょうど3個となるのは,右の図のようなときである. したがって,$7<a \leqq 8$よって,（ア）〜（ウ）より,求める$a$の値の範囲は$-7 \leqq a<-6,7<a \leqq 8$
