% 節末I5.1.1★★
右の図は,生徒数がいずれも40人のA組,B組,C組に100点満点の同じテストを行った結果を箱ひげ図に表したものである.次の(i)〜(iv)の記述のうち,適切ではないものを答えよ. (i)B組の合計得点はA組の合計得点より小さい. (ii)A組とB組において,得点が60点以上の人数は同じである. (iii)B組で得点が50点以上の人数は20人以上である. (iv)B組の生徒が,A組,B組,C組全体の最高得点をとっている.
% 節末I5.1.2★★
10人の社員に対して作業時間を記録した.記録したところ,作業時間の平均値は20,分散は4.5であった.しかし,この10人のうち2人の作業時間が右の表のように修正された.修正後の10人の作業時間の平均値と分散を求めよ. \begin{tabular}{|c||c|c|} \hline 社員&修正前&修正後\\ \hline A&18&22\\ \hline B&17&23\\ \hline \end{tabular}
% 節末I5.1.3★★
ある地域でA地区とB地区の2か所のうちどちらかに新しい公園を建設する案があり,住民投票の結果,B地区を支持した住民が60人中43人であった. 一般に,B地区の方が住民にとって望ましい建設地であると判断してよいであろうか.もしA地区とB地区を何も考えずに選ぶ場合,それぞれが選ばれる確率は0.5とし,起こる割合が$5\%$以下であればほとんど起こりえないと判断するものとする. ただし,$50\%$の確率で表が出る公正なコインを60枚投げて,表が出た枚数を記録する実験を1000セット行ったところ右の表のようになったとして,この結果を用いよ. \begin{tabular}{|c||c|} \hline 表の枚数&回数\\ \hline $0 \sim 30$&540\\\hline 31&99\\\hline 32&91\\\hline 33&86\\\hline 34&54\\\hline 35&43\\\hline 36&32\\\hline 37&20\\\hline 38&11\\\hline 39&8\\\hline 40&6\\\hline 41&4\\\hline 42&3\\\hline 43&2\\\hline 44&1\\\hline 45&0\\\hline 46&0\\\hline \end{tabular}
% 章末I5.1★★
任意の連続する4個の自然数の分散$s^2$を求めよ.
% 章末I5.2★★
変量$x$についてのデータの値が$p, q, r, s, t$であるとする.データ$p, q, r$の平均値が12,分散が4であり,データ$s, t$の平均値が10,分散が2であるとするとき,変量$x$の次の値を求めよ. (1)平均値 (2)分散
% 章末I5.3★★★
ある実験で得られた$n$個の測定値$x_1, x_2, x_3, \ldots, x_n$の平均が$m$,分散が$\sigma^2$である.$p, q(p>0, q>0)$を正の定数とするとき,次の問いに答えよ. (1)$\left(x_1-x\right)^2+\left(x_2-x\right)^2+\left(x_3-x\right)^2+\cdots+\left(x_n-x\right)^2$を最小にする$x$の値を求めよ. (2)$x_1+p, x_2+p, x_3+p, \ldots, x_n+p$の平均値および分散を求めよ. (3)$q x_1, q x_2, q x_3, \ldots, q x_n$の平均値および分散を求めよ.
% 章末I5.4★★★
ある学校で,120人の生徒が定期テストを受験した.得点の平均値が$m$点,標準偏差が$s$点である試験において,得点が$x$点である受験者の偏差値は$50+\frac{10(x-m)}{s}$で与えられる.Aさんのこのテストの得点は78点であり,偏差値は58であった.また,このテストの得点の平均値は66点であった. (1)120人の生徒の得点の標準偏差を求めよ. (2)後日,この定期テストを新たに60人が受験し,受験者数は合計で180人となった.その結果,試験の得点の平均値が67点となり,Aさんの偏差値は55となった.新たに受験した60人の受験者の得点について,平均値と標準偏差をそれぞれ求めよ.
% 章末I5.5★★★
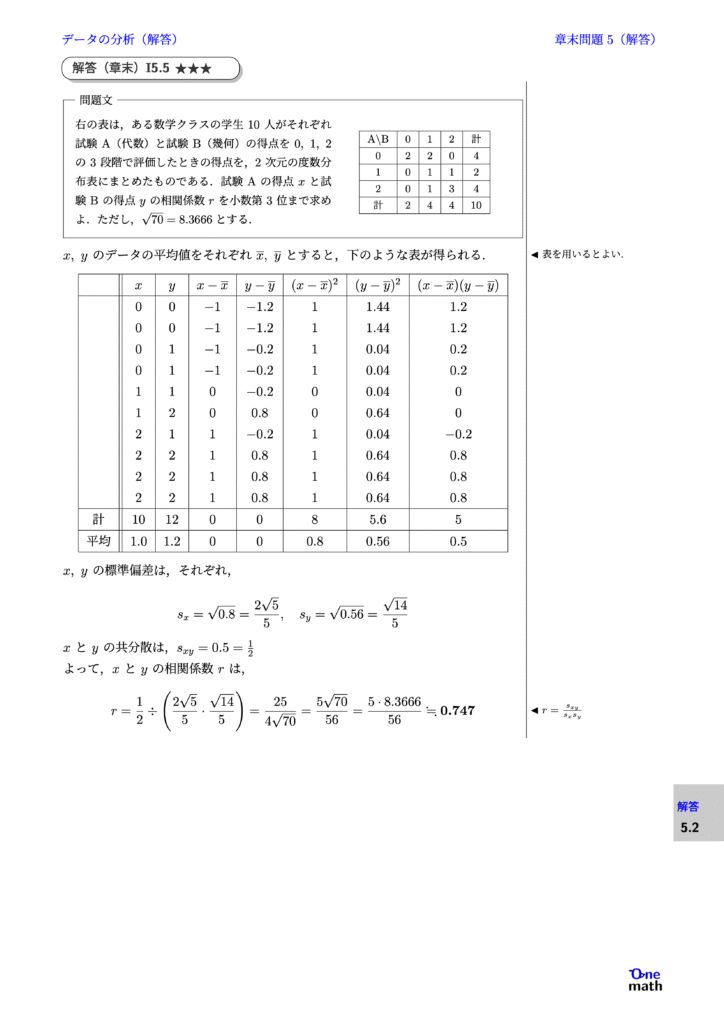
右の表は,ある数学クラスの学生10人がそれぞれ試験A(代数)と試験B(幾何)の得点を$0, 1, 2$の3段階で評価したときの得点を,2次元の度数分布表にまとめたものである.試験Aの得点$x$と試験Bの得点$y$の相関係数$r$を小数第3位まで求めよ.ただし,$\sqrt{70}=8.3666$とする. \begin{tabular}{|c|c|c|c|c|} \hline A\verb|\|B&0&1&2&計\\ \hline 0&2&2&0&4\\ \hline 1&0&1&1&2\\ \hline 2&0&1&3&4\\ \hline 計&2&4&4&10\\ \hline \end{tabular}
% 解答(節末)I5.1.1
(i)A組,B組の得点の平均値は,それぞれおおよそ55点,50点と読み取れる. A組,B組ともに人数は同じであるから,平均値が小さいB組の合計得点がA組より低く,適切である. (ii)A組,B組とも中央値が60点であるが,得点が60点以上の生徒の人数は箱ひげ図からは読み取れない. したがって,60点以上の人数が同じであるとは限らず,適切ではない. (iii)B組の得点の中央値は60点であるため,少なくとも20人が60点以上の得点をとっている. したがって,50点以上の人数は20人以上であるので,適切である. (iv)A組,B組,C組の得点の最大値は,それぞれ90点,100点,90点である. したがって,B組の最大得点が全体の最高得点であるため,適切である. よって,適切ではないものは,(ii)
% 解答(節末)I5.1.2
修正後の作業時間の平均値を$\overline{x}$,分散を$s_x{ }^2$,作業時間の2乗の平均値を$\overline{x^2}$とする. このとき, $ \overline{x}=\frac{1}{10}\{20 \times 10-(18+17)+(22+23)\}=21 (\text{時間}) $ 修正前の作業時間の平均値を$\overline{y}$,分散を$s_y{ }^2$,作業時間の2乗の平均値を$\overline{y^2}$とする. このとき,$ \overline{y^2}=s_y{ }^2+(\overline{y})^2 =4.5+20^2=404.5 $ したがって,$\overline{x^2}=\frac{1}{10}\left\{404.5 \times 10-\left(18^2+17^2\right)+\left(22^2+23^2\right)\right\}=444.5$ よって,$s_x{ }^2=\overline{x^2}-(\overline{x})^2=444.5-21^2=3.5$
% 解答(節末)I5.1.3
「B地区の方が望ましい建設地である」と判断してよいかを考察するために,これに反する「B地区の方が望ましい建設地とはいえない」という仮説を立てる. このとき,公正なコインの実験結果から,60枚中43枚以上が表となる場合の相対度数は, $$ \frac{2+1}{1000}=\frac{3}{1000}=0.003 $$ より,$0.3\%$ よって,これは$5\%$より小さいから,仮説は正しくなかったと考えられ,仮説は棄却される. すなわち,B地区の方が望ましい建設地であると判断してよい.
% 解答(章末)I5.1
$n$を自然数とすると,任意の連続する4個の自然数は,$n$,$n+1$,$n+2$,$n+3$とおける. 4個の自然数の平均値は, $$ \frac{1}{4}\{n+(n+1)+(n+2)+(n+3)\}=n+1.5 $$ よって,任意の連続する4個の自然数の分散は, $$ \begin{aligned} & \frac{1}{4}\left\{n^2+(n+1)^2+(n+2)^2+(n+3)^2\right\}-(n+1.5)^2 \\ =& \frac{1}{4}\left(4 n^2+12 n+14\right)-\left(n^2+3 n+2.25\right)\\ =& \frac{14}{4}-2.25=1.25 \end{aligned} $$
% 解答(章末)I5.2
(1)データ$p, q, r$の平均値が12であるから,$\frac{p+q+r}{3}=12$ すなわち,$p+q+r=36\cdots(\mathrm{i})$ データ$s, t$の平均値が10であるから, $ \frac{s+t}{2}=10$ すなわち,$s+t=20\cdots(\mathrm{ii})$ (i),(ii)の辺々を足し合わせると,$p+q+r+s+t=56$ よって,$x$の平均値$\overline{x}$は, $$ \overline{x}=\frac{p+q+r+s+t}{5}=\frac{56}{5}=11.2 $$ (2)データ$p, q, r$の分散が4であるから,$\frac{p^2+q^2+r^2}{3}-12^2=4$ すなわち,$p^2+q^2+r^2=444\cdots(\mathrm{iii})$ データ$s, t$の分散が2であるから,$\frac{s^2+t^2}{2}-10^2=2$ すなわち,$s^2+t^2=204\cdots(\mathrm{iv})$ (iii),(iv)の辺々を足し合わせると,$p^2+q^2+r^2+s^2+t^2=648$ よって,$x$の分散は, $$ \frac{p^2+q^2+r^2+s^2+t^2}{5}-\overline{x}^2 =\frac{648}{5}-11.2^2 =129.6-125.44 =4.16 $$
% 解答(章末)I5.3
(1)$\left(x_i-x\right)^2=x_i^2-2 x_i x+x^2(i=1, 2, \cdots, n)$ となることから,与えられた式を整理すると, $$ nx^2-2\left(x_1+x_2+\cdots+x_n\right)x+\left(x_1{}^2+x_2{}^2+\cdots+x_n{}^2\right) $$ したがって, $$\begin{aligned} &n x^2-2\left(x_1+x_2+\cdots+x_n\right)x+\left(x_1{}^2+x_2{}^2+\cdots+x_n{}^2\right)\\ &=n\left\{x-\frac{1}{n}\left(x_1+x_2+\cdots+x_n\right)\right\}^2-\frac{1}{n}\left(x_1+x_2+\cdots+x_n\right)^2\\ &+\left(x_1{}^2+x_2{}^2+\cdots+x_n{}^2\right) \end{aligned} $$ よって, $ x=\frac{1}{n}\left(x_1+x_2+\cdots+x_n\right) $のとき,すなわち,$x=m$ のとき,最小値をとる. (2) $ \begin{aligned} & \begin{aligned} \text {(平均値)} &=\frac{1}{n}\left\{\left(x_1+p\right)+\left(x_2+p\right)+\cdots+\left(x_n+p\right)\right\} \\ &=\frac{1}{n}\left\{\left(x_1+x_2+\cdots+x_n\right)+n p\right\}\\ &=\frac{1}{n}\left(x_1+x_2+\cdots+x_n\right)+p \\ &=m+p, \end{aligned} \\ & \begin{aligned} \text {(分散)}=& \frac{1}{n}\left\{\left(x_1+p\right)^2+\left(x_2+p\right)^2+\cdots+\left(x_n+p\right)^2\right\}-(m+p)^2 \\ =& \frac{1}{n}\left\{\left(x_1{}^2+x_2{}^2+\cdots+x_n{}^2\right)+2 p\left(x_1+x_2+\cdots+x_n\right)+n p^2\right\}\\ &-(m+p)^2 \\ =& \frac{1}{n}\left(x_1{}^2+x_2{}^2+\cdots+x_n{}^2\right)+2 p m+p^2-(m+p)^2 \\ =& \frac{1}{n}\left(x_1{}^2+x_2{}^2+\cdots+x_n{}^2\right)-m^2 \\ =& \sigma^2 \end{aligned} \end{aligned} $ (3) $ \begin{aligned} \text {(平均値)} &=\frac{1}{n}\left\{q x_1+q x_2+\cdots+q x_n\right\}=q \times \frac{1}{n}\left(x_1+x_2+\cdots+x_n\right)\\ &=q m, \\ \text {(分散)} &=\frac{1}{n}\left\{\left(q x_1\right)^2+\left(q x_2\right)^2+\cdots+\left(q x_n\right)^2\right\}-(q m)^2 \\ &=q^2 \frac{1}{n}\left(x_1{}^2+x_2{}^2+\cdots+x_n{}^2\right)-q^2 m^2\\ &=q^2\left(\sigma^2+m^2\right)-q^2 m^2 \\ &=q^2 \sigma^2 \end{aligned} $
% 解答(章末)I5.4
(1) 最初に受験した120人の得点の標準偏差を$s_x$とする. Aさんの偏差値より, $ 50+\frac{10(78-66)}{s_x}=58 $ よって,$s_x=15$ (2) 新たに受験した60人の得点の平均値を$\overline{y}$とする. 180人の得点の平均値より, $$ \frac{66 \times 120+\overline{y} \times 60}{120+60}=67 $$ よって,$\overline{y}=69$ 180人の得点の平均値を$\overline{z}$,標準偏差を$s_z$,得点の2乗の平均値を$\overline{z^2}$とする. Aさんの得点の偏差値より, $50+\frac{10(78-67)}{s_z}=55$ したがって,$s_z=22$ $s_z{}^2=\overline{z^2}-(\overline{z})^2$であるから, $$ \overline{z^2}=s_z{}^2+(\overline{z})^2=22^2+67^2=4973 $$ また,最初に受験した120人の得点の平均値を$\overline{x}$,得点の2乗の平均値を$\overline{x^2}$とすると,$s_x{}^2=\overline{x^2}-(\overline{x})^2$であるから, $$ \overline{x^2}=s_x{}^2+(\overline{x})^2=15^2+66^2=4581 $$ ゆえに,新たに受験した60人の得点の2乗の平均値を$\overline{y^2}$とすると, $$ \overline{y^2}=\frac{\overline{z^2} \times 180-\overline{x^2} \times 120}{60} =\frac{4973 \times 180-4581 \times 120}{60}=5757 $$ よって,新たに受験した60人の得点の標準偏差$s_y$は, $$ s_y=\sqrt{\overline{y^2}-(\overline{y})^2}=\sqrt{5757-69^2} =2\sqrt{249} $$
% 解答(章末)I5.5
$x, y$のデータの平均値をそれぞれ$\overline{x}, \overline{y}$とすると,下のような表が得られる. \begin{tabular}{|c||c|c|c|c|c|c|c|} \hline &$x$&$y$&$x-\overline{x}$&$y-\overline{y}$&$(x-\overline{x})^2$&$(y-\overline{y})^2$&$(x-\overline{x})(y-\overline{y})$\\ \hline &0&0&$-1$&$-1.2$&$1$&$1.44$&$1.2$\\ &0&0&$-1$&$-1.2$&$1$&$1.44$&$1.2$\\ &0&1&$-1$&$-0.2$&$1$&$0.04$&$0.2$\\ &0&1&$-1$&$-0.2$&$1$&$0.04$&$0.2$\\ &1&1&$0$&$-0.2$&$0$&$0.04$&$0$\\ &1&2&$0$&$0.8$&$0$&$0.64$&$0$\\ &2&1&$1$&$-0.2$&$1$&$0.04$&$-0.2$\\ &2&2&$1$&$0.8$&$1$&$0.64$&$0.8$\\ &2&2&$1$&$0.8$&$1$&$0.64$&$0.8$\\ &2&2&$1$&$0.8$&$1$&$0.64$&$0.8$\\ \hline 計&$10$&$12$&$0$&$0$&$8$&$5.6$&$5$\\ \hline 平均&$1.0$&$1.2$&$0$&$0$&$0.8$&$0.56$&$0.5$\\ \hline \end{tabular} $x, y$の標準偏差は,それぞれ, $$ s_x=\sqrt{0.8}=\frac{2\sqrt{5}}{5} , s_y=\sqrt{0.56}=\frac{\sqrt{14}}{5} $$ $x$と$y$の共分散は,$ s_{x y}=0.5=\frac{1}{2}$ よって,$x$と$y$の相関係数$r$は, $$ r=\frac{1}{2} \div \left(\frac{2\sqrt{5}}{5} \cdot \frac{\sqrt{14}}{5}\right)=\frac{25}{4\sqrt{70}}=\frac{5 \sqrt{70}}{56}=\frac{5 \cdot 8.3666}{56} \fallingdotseq 0.747 $$