リンク(関連例題)
あわせて読みたい


【数学A】例題3.1.6:オイラー線(One More)★★★
https://www.youtube.com/watch?v=yNGEFmin4f0 問題の解答 検索用コード(LaTeX) % 例題A3.1.6:オイラー線 (One More)★★★ 正三角形ではない鋭角三角形の$\triangle ...
あわせて読みたい
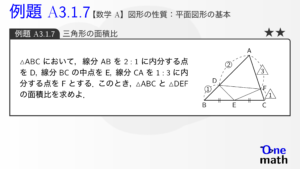

【数学A】例題3.1.7:三角形の面積比(One More)★★
https://www.youtube.com/watch?v=9KQeIefTi4o 問題の解答 検索用コード(LaTeX) % 例題A3.1.7:三角形の面積比 (One More)★★ $\triangle \mathrm{ABC}$において,線...
あわせて読みたい


【数学A】例題3.1.9:チェバの定理・メネラウスの定理の逆(One More)★★
https://www.youtube.com/watch?v=sOC8nDgJzdw 問題の解答 検索用コード(LaTeX) % 例題A3.1.9:チェバの定理・メネラウスの定理の逆 (One More)★★ $\triangle \math...
あわせて読みたい


【数学A】例題3.1.10:メネラウスの定理と面積比(One More)★★★
https://www.youtube.com/watch?v=07A666VS0sw 問題の解答 検索用コード(LaTeX) % 例題A3.1.10:メネラウスの定理と面積比 (One More)★★★ $\triangle \mathrm{ABC}$...
節末A3.1.1〜A3.1.4の解答

リンク(関連例題)
あわせて読みたい


【数学A】例題3.2.7:共通接線(One More)★★★
https://www.youtube.com/watch?v=8L4KLYaBok4 問題の解答 検索用コード(LaTeX) % 例題A3.2.7:共通接線 (One More)★★★ 右の図のように,半径6の円Oと半径10の円$\ma...
あわせて読みたい


【数学A】例題3.2.8:互いに接する円(One More)★★
https://www.youtube.com/watch?v=6yg5s_oAsT8 問題の解答 検索用コード(LaTeX) % 例題A3.2.8:互いに接する円 (One More)★★ 半径$6$の$2$つの円$\mathrm{A}$,$\mat...
あわせて読みたい


【数学A】例題3.2.11:2次方程式の解と作図(One More)★★
https://www.youtube.com/watch?v=p83Qb1tok-U 問題の解答 検索用コード(LaTeX) % 例題A3.2.11:2次方程式の解と作図 (One More)★★ 長さ$a,b$の線分が与えられたと...
節末A3.2.1〜A3.2.4の解答

リンク(関連例題)
あわせて読みたい


【数学A】例題3.3.1:直線と平面の垂直(One More)★★
https://www.youtube.com/watch?v=AU91EtVZm34 問題の解答 検索用コード(LaTeX) % 例題A3.3.1:直線と平面の垂直 (One More)★★ 正四面体ABCDについて,次のことを示...
あわせて読みたい


【数学A】例題3.3.2:三垂線の定理(One More)★★★
https://www.youtube.com/watch?v=Asu6UIyTC3s 問題の解答 検索用コード(LaTeX) % 例題A3.3.2:三垂線の定理 (One More)★★★ $l$を平面$\alpha$上の直線,$\mathrm{P}...
あわせて読みたい


【数学A】例題3.3.3:多面体の面・辺・頂点の数(One More)★★★
https://www.youtube.com/watch?v=nSshIhPd-yo 問題の解答 検索用コード(LaTeX) % 例題A3.3.3:多面体の面・辺・頂点の数 (One More)★★★ 正二十面体において,各辺の...
あわせて読みたい


【数学A】例題3.3.4:多面体の切断・体積(One More)★★★
https://www.youtube.com/watch?v=iVU5ztGBO7Q 問題の解答 検索用コード(LaTeX) % 例題A3.3.4:多面体の切断・体積 (One More)★★★ 1辺の長さが4の立方体$\mathrm{AB...
節末A3.3.1〜A3.3.4の解答

リンク(関連例題)
あわせて読みたい


【数学A】例題3.1.7:三角形の面積比(One More)★★
https://www.youtube.com/watch?v=9KQeIefTi4o 問題の解答 検索用コード(LaTeX) % 例題A3.1.7:三角形の面積比 (One More)★★ $\triangle \mathrm{ABC}$において,線...
あわせて読みたい


【数学A】例題3.3.3:多面体の面・辺・頂点の数(One More)★★★
https://www.youtube.com/watch?v=nSshIhPd-yo 問題の解答 検索用コード(LaTeX) % 例題A3.3.3:多面体の面・辺・頂点の数 (One More)★★★ 正二十面体において,各辺の...
あわせて読みたい


【数学A】例題3.3.4:多面体の切断・体積(One More)★★★
https://www.youtube.com/watch?v=iVU5ztGBO7Q 問題の解答 検索用コード(LaTeX) % 例題A3.3.4:多面体の切断・体積 (One More)★★★ 1辺の長さが4の立方体$\mathrm{AB...
章末A3.1〜A3.4の解答

検索用コード(LaTeX)
% 節末A3.1.1★★
$\triangle \mathrm{ABC}$の辺$\mathrm{BC},\mathrm{CA},\mathrm{AB}$の中点をそれぞれ$\mathrm{D},\mathrm{E},\mathrm{F}$とすると,$\triangle \mathrm{ABC}$の外心Oは,$\triangle \mathrm{DEF}$の垂心であることを証明せよ.
% 節末A3.1.2★★
右の図において,$\triangle \mathrm{ABC}$の重心をGとするとき,$\triangle \mathrm{ABC}$の面積と四角形ARGQの面積比を求めよ.
% 節末A3.1.3★★
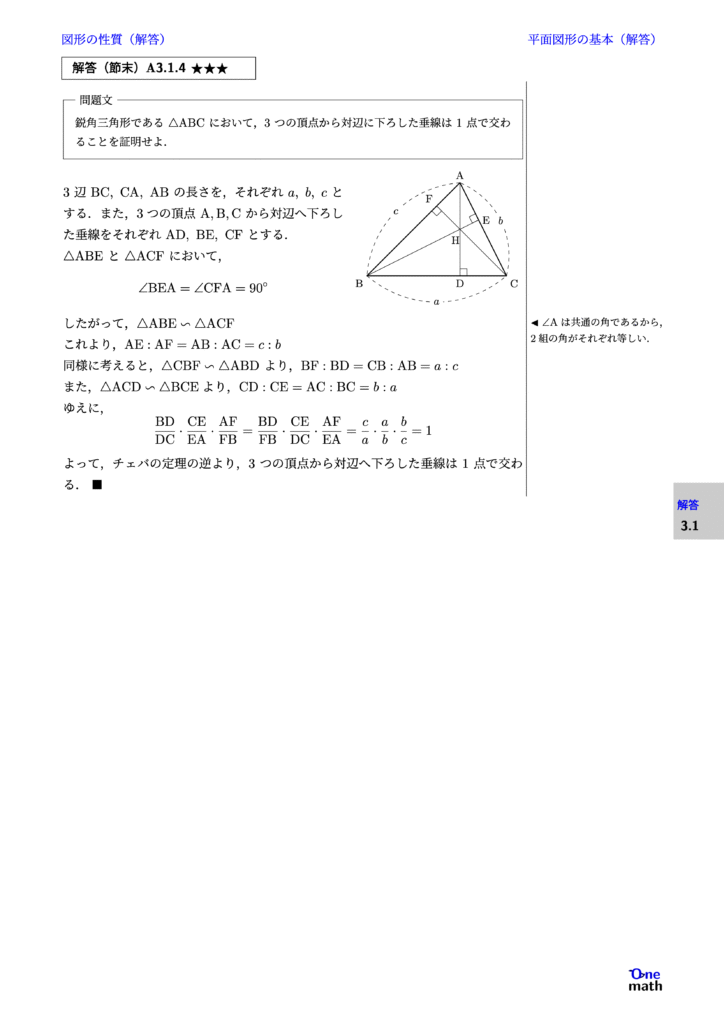
鋭角三角形である$\triangle \mathrm{ABC}$において,3つの頂点から対辺に下ろした垂線は1点で交わることを証明せよ.
% 節末A3.1.4★★★
$\triangle \mathrm{ABC}$の辺$\mathrm{BC,CA,AB}$を$2: 1$に内分する点をそれぞれ$\mathrm{D,E,F}$とし,$\mathrm{AD}$と$\mathrm{BE}$,$\mathrm{BE}$と$\mathrm{CF}$,$\mathrm{CF}$と$\mathrm{AD}$の交点をそれぞれ$\mathrm{P,Q,R}$とする.このとき,次の問いに答えよ. (1)$\mathrm{AP}: \mathrm{PR}: \mathrm{RD}=3:x:y$とするとき,$x,y$の値を求めよ. (2)$\triangle \mathrm{ABC}$と$\triangle \mathrm{PQR}$の面積比を求めよ.
% 節末A3.2.1★★★
$\triangle \mathrm{ABC}$の内心を$\mathrm{I},\triangle \mathrm{BCI}$の外心を$\mathrm{O}$とする.4点$\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{O}$は同一円周上にあることを示せ.
% 節末A3.2.2★★
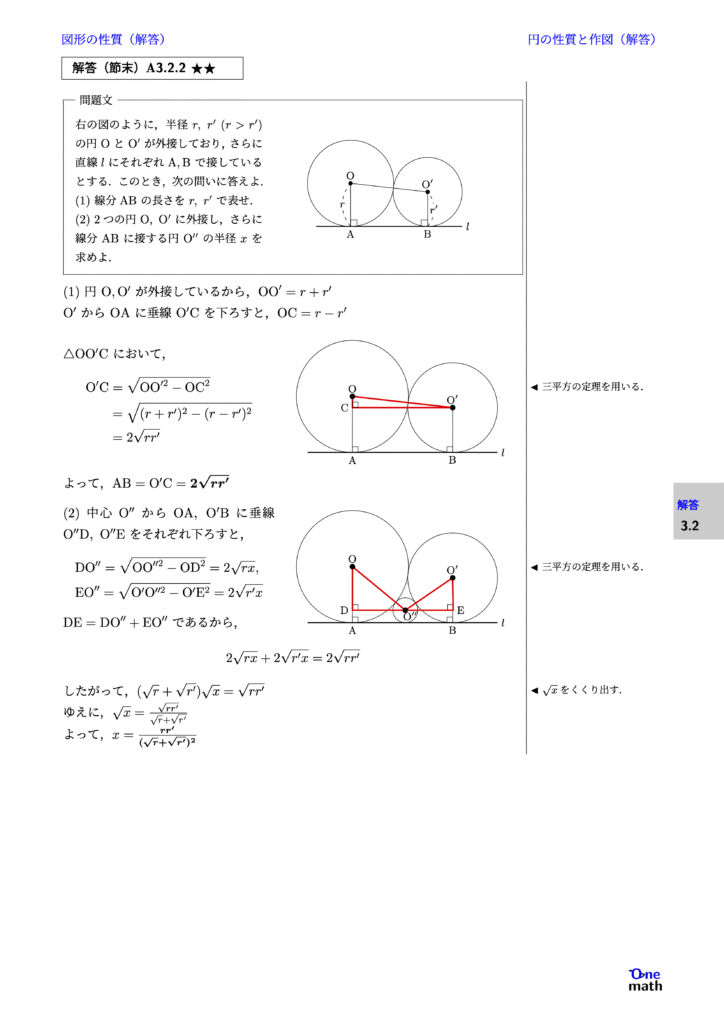
右の図のように,半径$r,r^{\prime} (r>r^{\prime})$の円$\mathrm{O}$と$\mathrm{O}^{\prime}$が外接しており,さらに直線$l$にそれぞれ$\mathrm{A},\mathrm{B}$で接しているとする.このとき,次の問いに答えよ. (1)線分$\mathrm{AB}$の長さを$r,r^{\prime}$で表せ. (2)2つの円$\mathrm{O},\mathrm{O}^{\prime}$に外接し,さらに線分$\mathrm{AB}$に接する円$\mathrm{O}^{\prime \prime}$の半径$x$を求めよ.
% 節末A3.2.3★★
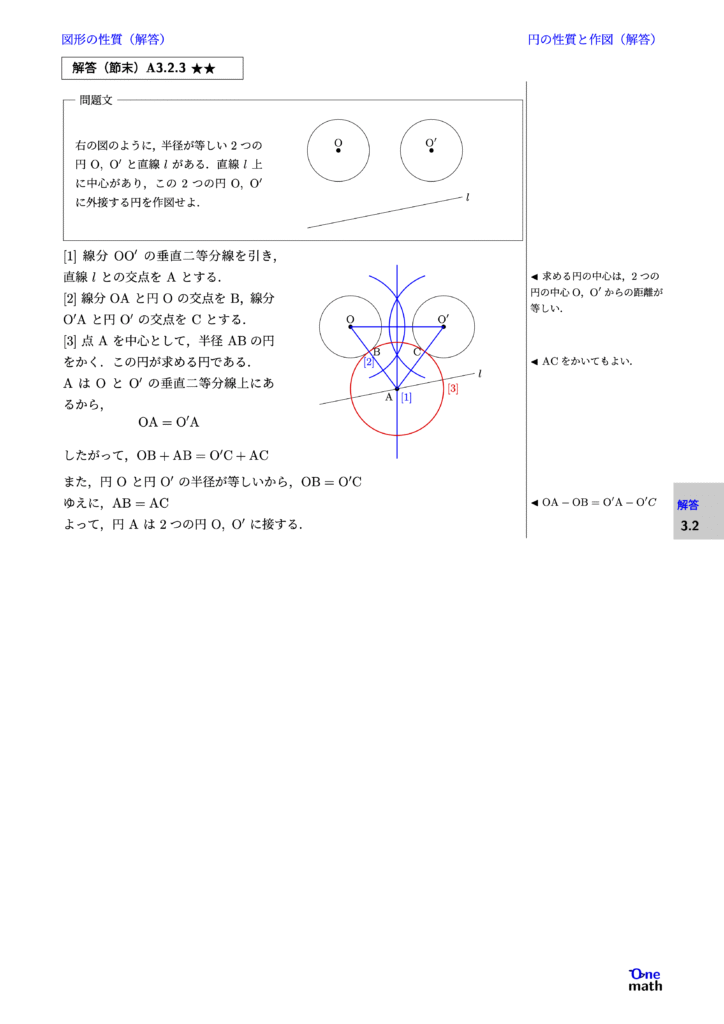
右の図のように,半径が等しい2つの円$\mathrm{O},\mathrm{O}^{\prime}$と直線$l$がある.直線$l$上に中心があり,この2つの円$\mathrm{O},\mathrm{O}^{\prime}$に外接する円を作図せよ.
% 節末A3.2.4★★
長さ3の線分が与えられたとき,連立方程式$x+y=3,x y=1$の解を長さとする線分を作図せよ.
% 節末A3.3.1★★
正四面体$\mathrm{ABCD}$において,向かい合う2辺$\mathrm{AB}$と$\mathrm{CD}$は垂直であることを示せ.
% 節末A3.3.2★★
正四面体$\mathrm{OABC}$において,辺$\mathrm{AB}$の中点を$\mathrm{M}$とし,頂点$\mathrm{O}$から線分$\mathrm{CM}$に下ろした垂線を$\mathrm{OH}$とする.このとき,$\mathrm{OH} \perp$平面$\mathrm{ABC}$であることを示せ.
% 節末A3.3.3★★★
1辺の長さが3の正四面体がある.この正四面体を右の図のように,1つの頂点に集まる3つの辺においてそれぞれ3等分した点のうち,頂点に近い方の点を結んでできる正三角形を含む平面で切り,頂点を含む正四面体を取り除く.すべての頂点において同様に正四面体を取り除いたとき,残った立体の体積$V$を求めよ.
% 節末A3.3.4★★★
1辺の長さが$a$の正四面体$\mathrm{ABCD}$の2辺$\mathrm{AB},\mathrm{CD}$の中点をそれぞれ$\mathrm{M},\mathrm{N}$とする.2直線CM,DMのなす角を$\alpha$,2直線$\mathrm{MN},\mathrm{AC}$のなす角を$\beta$とするとき,$\cos \alpha$と$\beta$を求めよ.
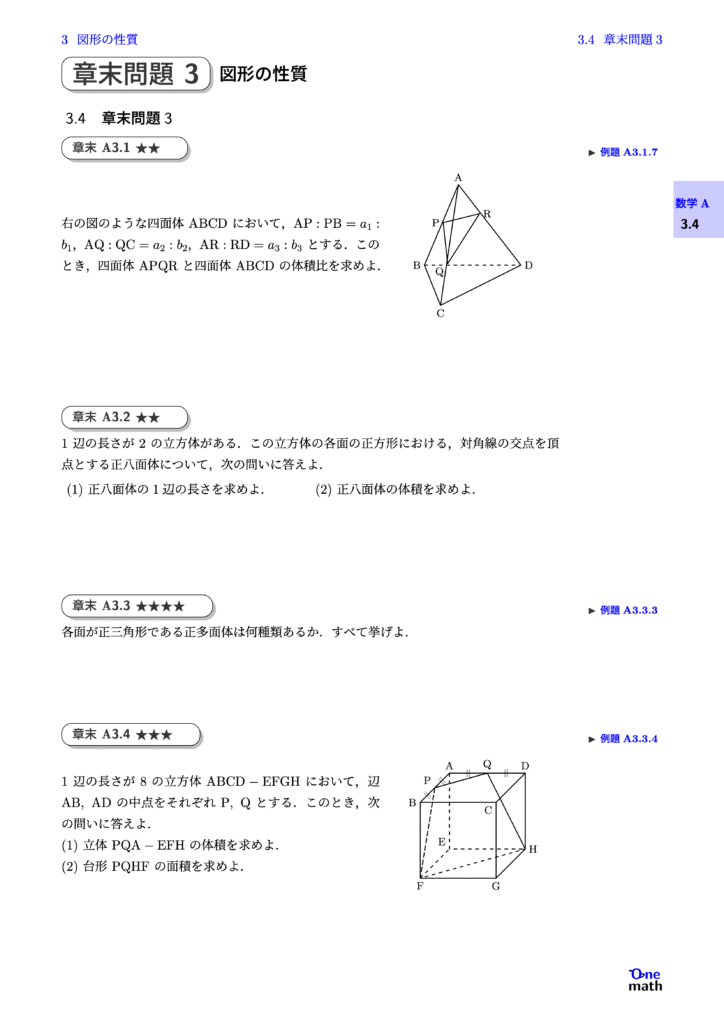
% 章末A3.1★★
右の図のような四面体$\mathrm{ABCD}$において,$\mathrm{AP}: \mathrm{PB}=a_1: b_1$,$\mathrm{AQ}: \mathrm{QC}=a_2: b_2$,$\mathrm{AR}: \mathrm{RD}=a_3: b_3$とする.このとき,四面体$\mathrm{APQR}$と四面体$\mathrm{ABCD}$の体積比を求めよ.
% 章末A3.2★★
1辺の長さが2の立方体がある.この立方体の各面の正方形における,対角線の交点を頂点とする正八面体について,次の問いに答えよ. (1)正八面体の1辺の長さを求めよ. (2)正八面体の体積を求めよ.
% 章末A3.3★★★★
各面が正三角形である正多面体は何種類あるか.すべて挙げよ.
% 章末A3.4★★★
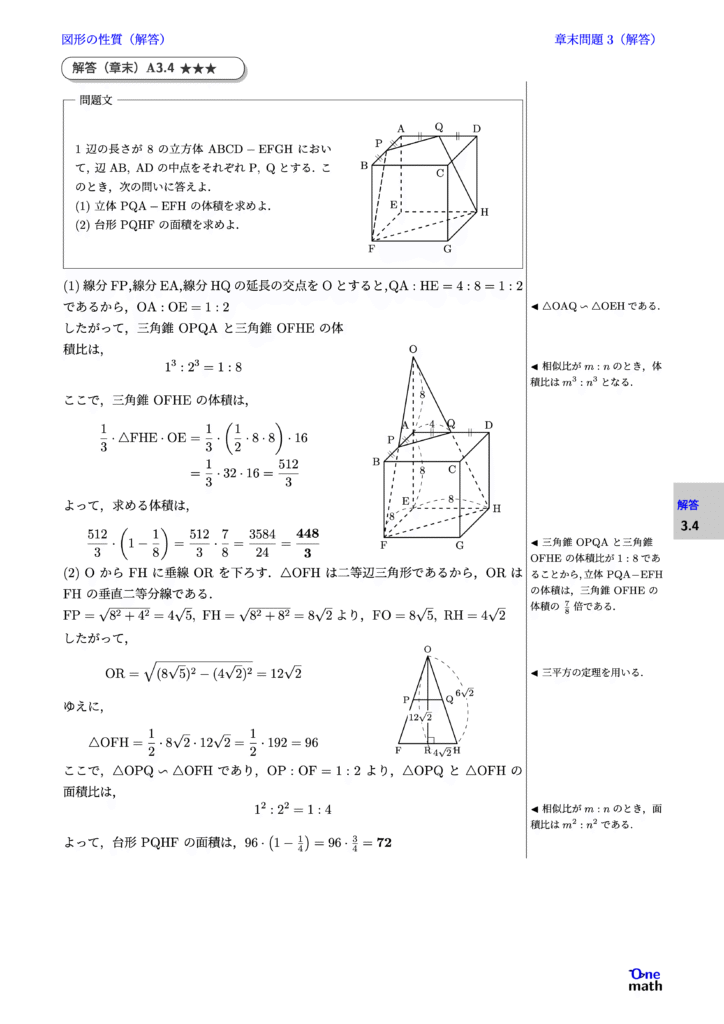
1辺の長さが8の立方体$\mathrm{ABCD}-\mathrm{EFGH}$において,辺$\mathrm{AB},\mathrm{AD}$の中点をそれぞれ$\mathrm{P},\mathrm{Q}$とする.このとき,次の問いに答えよ. (1)立体$\mathrm{PQA}-\mathrm{EFH}$の体積を求めよ. (2)台形$\mathrm{PQHF}$の面積を求めよ.
% 解答(節末)A3.1.1
Oは$\triangle \mathrm{ABC}$の外心であり,DはBCの中点であるから, $\mathrm{OD} \perp \mathrm{BC}\cdots(\mathrm{i})$ また,中点連結定理より, $$ \mathrm{FE} \parallel \mathrm{BC}\cdots(\mathrm{ii}) $$ (i),(ii)より,$\mathrm{OD} \perp \mathrm{FE}$ 同様にして, $$ \mathrm{OE} \perp \mathrm{FD}, \mathrm{OF} \perp \mathrm{DE} $$ よって,Oは$\triangle \mathrm{DEF}$の垂心である.$ \blacksquare$
% 解答(節末)A3.1.2
$(\text{四角形 ARGQ})=\triangle \mathrm{ABC}-\triangle \mathrm{CBR}-\triangle \mathrm{CGQ} \cdots(\mathrm{i})$ また,Gは重心より,Rは辺ABの中点であるから, $$ \triangle \mathrm{CBR}=\frac{1}{2} \triangle \mathrm{ABC}\cdots(\mathrm{ii}) $$ また,$\triangle \mathrm{CGQ}: \triangle \mathrm{CRA}=\mathrm{CG} \cdot \mathrm{CQ}: \mathrm{CR} \cdot \mathrm{CA}$ Gは重心より,$\mathrm{CG}: \mathrm{CR}=2: 3,\mathrm{CQ}: \mathrm{CA}=1: 2$であるから, $$ \triangle \mathrm{CGQ} =\frac{2 \cdot 1}{3 \cdot 2} \triangle \mathrm{CRA}=\frac{1}{3} \triangle \mathrm{CRA} =\frac{1}{3} \cdot \frac{1}{2} \triangle \mathrm{ABC}=\frac{1}{6} \triangle \mathrm{ABC}\cdots(\mathrm{iii}) $$ (ii),(iii)を(i)に代入すると, $$(\text{四角形 ARGQ})=\triangle \mathrm{ABC}-\frac{1}{2} \triangle \mathrm{ABC}-\frac{1}{6} \triangle \mathrm{ABC} =\frac{1}{3} \triangle \mathrm{ABC} $$ よって,$\triangle \mathrm{ABC}$の面積と四角形ARGQの面積比は,$3: 1$
% 解答(節末)A3.1.3
3辺$\mathrm{BC},\mathrm{CA},\mathrm{AB}$の長さを,それぞれ$a,b,c$とする.また,3つの頂点$\mathrm{A,B,C}$から対辺へ下ろした垂線をそれぞれ$\mathrm{AD,BE,CF}$とする. $\triangle \mathrm{ABE}$と$\triangle \mathrm{ACF}$において, $$\angle \mathrm{BEA}=\angle \mathrm{CFA}=90^{\circ}$$ したがって,$\triangle \mathrm{ABE} \backsim \triangle \mathrm{ACF}$ これより,$\mathrm{AE}:\mathrm{AF}=\mathrm{AB}:\mathrm{AC}=c:b$ 同様に考えると,$\triangle \mathrm{CBF} \backsim \triangle \mathrm{ABD}$より,$\mathrm{BF}:\mathrm{BD}=\mathrm{CB}:\mathrm{AB}=a:c$ また,$ \triangle \mathrm{ACD} \backsim \triangle \mathrm{BCE}$より,$\mathrm{CD}:\mathrm{CE}=\mathrm{AC}:\mathrm{BC}=b:a $ ゆえに, $$ \frac{\mathrm{BD}}{\mathrm{DC}} \cdot \frac{\mathrm{CE}}{\mathrm{EA}} \cdot \frac{\mathrm{AF}}{\mathrm{FB}} = \frac{\mathrm{BD}}{\mathrm{FB}} \cdot \frac{\mathrm{CE}}{\mathrm{DC}} \cdot \frac{\mathrm{AF}}{\mathrm{EA}} = \frac{c}{a} \cdot \frac{a}{b} \cdot \frac{b}{c}=1 $$ よって,チェバの定理の逆より, 3つの頂点から対辺へ下ろした垂線は1点で交わる.$ \blacksquare$
% 解答(節末)A3.1.4
(1)$\triangle \mathrm{ABD}$と直線CFについて,メネラウスの定理より, $$ \frac{\mathrm{AF}}{\mathrm{FB}} \cdot \frac{\mathrm{BC}}{\mathrm{CD}} \cdot \frac{\mathrm{DR}}{\mathrm{RA}}=1 $$ $ \frac{2}{1} \cdot \frac{3}{1} \cdot \frac{y}{x+3}=1 $ より,$x-6y=-3 \cdots(\mathrm{i})$ また,$\triangle \mathrm{ACD}$と直線BEについて,メネラウスの定理より, $$ \frac{\mathrm{AE}}{\mathrm{EC}} \cdot \frac{\mathrm{CB}}{\mathrm{BD}} \cdot \frac{\mathrm{DP}}{\mathrm{PA}}=1 $$ $ \frac{1}{2} \cdot \frac{3}{2} \cdot \frac{y+x}{3}=1 $より,$x+y=4 \cdots(\mathrm{ii})$ よって,(i),(ii)より,$x=3,y=1$ (2)(1)と同様に,$\mathrm{BQ}:\mathrm{QP}:\mathrm{PM}=3:3:1$より,$\triangle \mathrm{PBR}=\frac{3}{7} \triangle \mathrm{ABD}$ $\triangle \mathrm{ABD}=\frac{2}{3} \triangle \mathrm{ABC}$であるから, $$ \triangle \mathrm{PBR}=\frac{3}{7}\triangle \mathrm{ABD}=\frac{3}{7} \cdot \frac{2}{3}\triangle \mathrm{ABC}=\frac{2}{7} \triangle \mathrm{ABC} $$ また,$\triangle \mathrm{PQR}=\frac{3}{6} \triangle \mathrm{PBR}$であるから, $$ \triangle \mathrm{PQR}=\frac{3}{6} \triangle \mathrm{PBR}=\frac{3}{6} \cdot \frac{2}{7}\triangle \mathrm{ABC}=\frac{1}{7} \triangle \mathrm{ABC} $$ よって, $$ \triangle \mathrm{ABC}:\triangle \mathrm{PQR}=\triangle \mathrm{ABC}:\frac{1}{7} \triangle \mathrm{ABC}=7:1 $$ 別解: $\triangle \mathrm{ABP}=\frac{3}{7} \triangle \mathrm{ABD}=\frac{3}{7} \cdot \frac{2}{3} \triangle \mathrm{ABC}=\frac{2}{7} \triangle \mathrm{ABC}$ $\triangle \mathrm{BCQ},\triangle \mathrm{CAR}$も同様に, $$\triangle \mathrm{BCQ}=\triangle \mathrm{CAR}=\frac{2}{7} \triangle \mathrm{ABC}$$ したがって, $\triangle \mathrm{PQR} =\triangle \mathrm{ABC}-(\triangle \mathrm{ABP}+\triangle \mathrm{BCQ}+\triangle \mathrm{CAR}) =\frac{1}{7}\triangle \mathrm{ABC}$ よって,$\triangle \mathrm{ABC}$と$\triangle \mathrm{PQR}$の面積比は, $$ \triangle \mathrm{ABC}:\triangle \mathrm{PQR}=\triangle \mathrm{ABC}:\frac{1}{7} \triangle \mathrm{ABC}=7:1 $$
% 解答(節末)A3.2.1
点$\mathrm{I}$が$\triangle \mathrm{ABC}$の内心であるから, $$ \angle \mathrm{IBC}=\angle \mathrm{IBA},\angle \mathrm{ICB}=\angle \mathrm{ICA} $$ したがって, $$ \begin{aligned} \angle \mathrm{IBC}+\angle \mathrm{ICB} & =\frac{1}{2} \angle \mathrm{ABC}+\frac{1}{2} \angle \mathrm{ACB} \\ & =\frac{1}{2}(\angle \mathrm{ABC}+\angle \mathrm{ACB}) \\ & =\frac{1}{2}\left(180^{\circ}-\angle \mathrm{BAC}\right)\\ &=90^{\circ}-\frac{1}{2} \angle \mathrm{BAC} \cdots(\mathrm{i}) \end{aligned} $$ また,点$\mathrm{O}$が$\triangle \mathrm{BCI}$の外心であるから$\mathrm{OB}=\mathrm{OI}=\mathrm{OC}$ ゆえに,$\angle \mathrm{BOI}=180^{\circ}-2 \angle \mathrm{BIO},\angle \mathrm{COI}=180^{\circ}-2 \angle \mathrm{CIO}$ したがって, $$ \begin{aligned} \angle \mathrm{BOC} & =\angle \mathrm{BOI}+\angle \mathrm{COI} \\ & =\left(180^{\circ}-2 \angle \mathrm{BIO}\right)+\left(180^{\circ}-2 \angle \mathrm{CIO}\right) \\ & =360^{\circ}-2(\angle \mathrm{BIO}+\angle \mathrm{CIO})\\ &=360^{\circ}-2 \angle \mathrm{BIC} \cdots(\mathrm{ii}) \end{aligned} $$ ここで,(i)より, $$ \begin{aligned} \angle \mathrm{BIC} & =180^{\circ}-(\angle \mathrm{IBC}+\angle \mathrm{ICB}) \\ & =180^{\circ}-\left(90^{\circ}-\frac{1}{2} \angle \mathrm{BAC}\right)\\ &=90^{\circ}+\frac{1}{2} \angle \mathrm{BAC} \end{aligned} $$ これを(ii)に代入すると, $$ \angle \mathrm{BOC}=360^{\circ}-2\left(90^{\circ}+\frac{1}{2} \angle \mathrm{BAC}\right)=180^{\circ}-\angle \mathrm{BAC} $$ ゆえに,$\angle \mathrm{BOC}+\angle \mathrm{BAC}=180^{\circ}$ よって,四角形$\mathrm{ABCO}$は円に内接する, すなわち,4点$\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{O}$は同一円周上にある.$ \blacksquare$
% 解答(節末)A3.2.2
(1)円$\mathrm{O},\mathrm{O}^{\prime}$が外接しているから, $ \mathrm{OO}^{\prime}=r+r^{\prime} $ $\mathrm{O}^{\prime}$から$\mathrm{OA}$に垂線$\mathrm{O}^{\prime} \mathrm{C}$を下ろすと, $ \mathrm{OC}=r-r^{\prime} $ $\triangle \mathrm{O}\mathrm{O}^{\prime} \mathrm{C}$において, $$ \begin{aligned} \mathrm{O}^{\prime} \mathrm{C} & =\sqrt{\mathrm{OO}^{\prime 2}-\mathrm{OC}^2} \\ & =\sqrt{(r+r^{\prime})^2-(r-r^{\prime})^2}\\ &=2 \sqrt{r r^{\prime}} \end{aligned} $$ よって,$\mathrm{AB}=\mathrm{O}^{\prime} \mathrm{C}={2} \sqrt{{r} {r}^{\prime}}$ (2)中心$\mathrm{O}^{\prime \prime}$から$\mathrm{OA},\mathrm{O}^{\prime} \mathrm{B}$に垂線$\mathrm{O}^{\prime \prime} \mathrm{D},\mathrm{O}^{\prime \prime} \mathrm{E}$をそれぞれ下ろすと, $$ \begin{aligned} & \mathrm{DO}^{\prime \prime}=\sqrt{\mathrm{OO}^{\prime\prime 2}-\mathrm{OD}^2}=2 \sqrt{r x},\\ & \mathrm{EO}^{\prime \prime}=\sqrt{\mathrm{O}^{\prime} \mathrm{O}^{\prime\prime 2}-\mathrm{O}^{\prime} \mathrm{E}^2}=2 \sqrt{r^{\prime} x} \end{aligned} $$ $\mathrm{DE}=\mathrm{DO}^{\prime \prime}+\mathrm{EO}^{\prime \prime}$であるから, $$ 2 \sqrt{r x}+2 \sqrt{r^{\prime} x}=2 \sqrt{r r^{\prime}} $$ したがって, $(\sqrt{r}+\sqrt{r^{\prime}}) \sqrt{x}=\sqrt{r r^{\prime}}$ ゆえに,$\sqrt{x}=\frac{\sqrt{r r^{\prime}}}{\sqrt{r}+\sqrt{r^{\prime}}}$ よって,$x=\frac{r r^{\prime}}{(\sqrt{r}+\sqrt{r^{\prime}})^2}$
% 解答(節末)A3.2.3
[1]線分$\mathrm{OO}^{\prime}$の垂直二等分線を引き, 直線$l$との交点を$\mathrm{A}$とする. [2]線分$\mathrm{OA}$と円$\mathrm{O}$の交点を$\mathrm{B}$,線分$\mathrm{O}^{\prime}\mathrm{A}$と円$\mathrm{O}^{\prime}$の交点を$\mathrm{C}$とする. [3]点$\mathrm{A}$を中心として,半径$\mathrm{AB}$の円をかく.この円が求める円である. $\mathrm{A}$は$\mathrm{O}$と$\mathrm{O}^{\prime}$の垂直二等分線上にあるから,$$\mathrm{OA}=\mathrm{O}^{\prime}\mathrm{A}$$ したがって, $ \mathrm{OB}+\mathrm{AB}=\mathrm{O}^{\prime}\mathrm{C}+\mathrm{AC} $ また,円$\mathrm{O}$と円$\mathrm{O}^{\prime}$の半径が等しいから, $ \mathrm{OB}=\mathrm{O}^{\prime}\mathrm{C} $ ゆえに, $ \mathrm{AB}=\mathrm{AC} $ よって,円$\mathrm{A}$は2つの円$\mathrm{O},\mathrm{O}^{\prime}$に接する.
% 解答(節末)A3.2.4
[1]長さ3の線分$\mathrm{AB}$を直径とする半円をかく. [2]線分$\mathrm{AB}$に平行で,線分$\mathrm{AB}$との距離が1である直線と,[1]の半円との交点の1つを$\mathrm{C}$とする. [3]$\mathrm{C}$から線分$\mathrm{AB}$に垂線を引き,その交点を$\mathrm{D}$とすると,線分$\mathrm{AD},\mathrm{BD}$が求める線分である. $\mathrm{AD}=x,\mathrm{BD}=y$とすると,$\mathrm{AD}+\mathrm{BD}=\mathrm{AB}$より, $$ x+y=3 $$ また,方べきの定理より,$\mathrm{AD} \cdot \mathrm{DB}=\mathrm{CD}^2$であるから, $ x y=1 $ よって,線分$\mathrm{AD},\mathrm{BD}$は連立方程式$x+y=3,x y=1$の解を長さとする線分である.
% 解答(節末)A3.3.1
辺$\mathrm{AB}$と辺$\mathrm{CD}$の中点をそれぞれ$\mathrm{M}$,$\mathrm{N}$とすると,$\triangle \mathrm{NAB}$は$\mathrm{NA}=\mathrm{NB}$の二等辺三角形であるから, $$ \mathrm{MN} \perp \mathrm{AB}\cdots(\mathrm{i}) $$ また,$\triangle \mathrm{CAB}$は$\mathrm{CA}=\mathrm{CB}$の二等辺三角形であるから, $$ \mathrm{CM} \perp \mathrm{AB}\cdots(\mathrm{ii}) $$ したがって,(i),(ii)より,$\mathrm{AB}$は直線$\mathrm{MN}$,$\mathrm{CM}$を含む平面$\mathrm{MCD}$に垂直である. $\mathrm{AB}$は平面$\mathrm{MCD}$上にある直線$\mathrm{CD}$に垂直である,すなわち,向かい合う2辺ABとCDは垂直である.$ \blacksquare$
% 解答(節末)A3.3.2
辺CMは正三角形である$\triangle \mathrm{CAB}$の中線であるから, $$ \mathrm{CM} \perp \mathrm{AB}\cdots(\mathrm{i}) $$ 辺OMは正三角形である$\triangle \mathrm{OAB}$の中線であるから, $$ \mathrm{OM} \perp \mathrm{AB} \cdots(\mathrm{ii}) $$ また,与えられた条件より,$\mathrm{OH} \perp \mathrm{CM}$であるから, $$ \mathrm{OH} \perp \mathrm{HM} \cdots(\mathrm{iii}) $$ (i)〜(iii)より,三垂線の定理を用いて, $ \mathrm{OH} \perp \text{平面 } \mathrm{ABC}$である.$ \blacksquare $
% 解答(節末)A3.3.3
\index{せっちょうしめんたい@切頂四面体} 右の図のように,正四面体$\mathrm{OABC}$の頂点$\mathrm{O}$から底面$\mathrm{ABC}$に垂線を下ろすと,その足$\mathrm{H}$は,正三角形$\mathrm{ABC}$の重心と一致する. 辺$\mathrm{BC}$の中点を$\mathrm{M}$とすると, $$ \mathrm{AH} = \frac{2}{3} \mathrm{AM} = \frac{2}{3} \cdot \frac{\sqrt{3}}{2} \mathrm{AB} = \sqrt{3} $$ したがって, $$ \mathrm{OH} = \sqrt{\mathrm{OA}^2 - \mathrm{AH}^2} = \sqrt{3^2 - (\sqrt{3})^2} = \sqrt{6} $$ 正四面体$\mathrm{OABC}$の体積を$V_0$とすると, $$ V_0 = \frac{1}{3} \cdot \triangle \mathrm{ABC} \cdot \mathrm{OH} = \frac{1}{3} \cdot \left(\frac{1}{2} \cdot 3 \cdot \frac{3 \sqrt{3}}{2}\right) \cdot \sqrt{6} = \frac{9 \sqrt{2}}{4} $$ また,取り除かれる正四面体の1辺の長さは1であるから,その体積を$V_1$とすると, $$ V_1 = \frac{1}{3} \cdot \left(\frac{1}{2} \cdot 1 \cdot \frac{\sqrt{3}}{2}\right) \cdot \sqrt{1^2 - \left(\frac{\sqrt{3}}{3}\right)^2} = \frac{\sqrt{2}}{12} $$ 取り除かれる正四面体の数は正四面体の頂点の数と同じであるから,4個取り除かれる. よって,残った立体の体積$V$は, $$ V = V_0 - 4 V_1 = \frac{9 \sqrt{2}}{4} - 4 \cdot \frac{\sqrt{2}}{12} = \frac{23 \sqrt{2}}{12} $$
% 解答(節末)A3.3.4
CMとDMのなす角$\alpha$は$\angle \mathrm{CMD}$に等しい. ここで,$\angle \mathrm{AMD} = 90^\circ$より, $$ \mathrm{CM} = \mathrm{DM} = \sqrt{a^2 - \left(\frac{a}{2}\right)^2} = \frac{\sqrt{3}}{2} a $$ したがって,$\triangle \mathrm{CMD}$において余弦定理を用いると, $$ \cos \alpha = \frac{\mathrm{CM}^2 + \mathrm{DM}^2 - \mathrm{CD}^2}{2 \cdot \mathrm{CM} \cdot \mathrm{DM}} = \frac{\frac{3}{4} a^2+\frac{3}{4} a^2 - a^2}{2 \cdot \left(\frac{\sqrt{3}}{2} a\right)\cdot \left(\frac{\sqrt{3}}{2} a\right)} = \frac{1}{3} $$ また, 辺$\mathrm{BC}$の中点を$\mathrm{L}$とすると,$\mathrm{AC} \parallel \mathrm{ML}$であることから,$\mathrm{MN}$と$\mathrm{AC}$のなす角$\beta$は$\angle \mathrm{LMN}$に等しい. ここで,$\angle \mathrm{CNM} = 90^\circ$より, $$ \mathrm{MN} = \sqrt{\mathrm{CM}^2 - \mathrm{CN}^2} = \sqrt{\left(\frac{\sqrt{3}}{2} a\right)^2 - \left(\frac{a}{2}\right)^2} = \frac{a}{\sqrt{2}} $$ $\mathrm{ML} = \mathrm{LN} = \frac{a}{2}$であるから,$\triangle \mathrm{LNM}$において余弦定理を用いると, $$ \cos \beta = \frac{\mathrm{ML}^2 + \mathrm{MN}^2 - \mathrm{LN}^2}{2 \cdot \mathrm{ML} \cdot \mathrm{MN}} = \frac{\left(\frac{a}{{2}}\right)^2+\left(\frac{a}{\sqrt{2}}\right)^2-\left(\frac{a}{{2}}\right)^2}{2 \cdot \frac{a}{2} \cdot \frac{a}{\sqrt{2}}} = \frac{1}{\sqrt{2}} $$ よって,$\beta = 45^\circ$
% 解答(章末)A3.1
$$ \triangle \mathrm{AQR}: \triangle \mathrm{ACD} =\mathrm{AQ} \cdot \mathrm{AR}: \mathrm{AC} \cdot \mathrm{AD} =a_2 a_3:\left(a_2+b_2\right)\left(a_3+b_3\right)\cdots(\mathrm{i}) $$ $\mathrm{B}$から面$\mathrm{ACD}$に下ろした垂線の足を$\mathrm{M}$,$\mathrm{P}$から面$\mathrm{ACD}$に下ろした垂線の足を$\mathrm{N}$とすると, $$ \mathrm{PN}: \mathrm{BM}=\mathrm{AP}: \mathrm{AB}=a_1:\left(a_1+b_1\right)\cdots(\mathrm{ii}) $$ よって,(i),(ii)より,求める体積比は, $$ a_2 a_3 \cdot a_1:\left(a_2+b_2\right)\left(a_3+b_3\right) \cdot\left(a_1+b_1\right) = a_1 a_2 a_3:\left({a}_1+b_1\right)\left({a}_2+b_2\right)\left({a}_3+b_3\right) $$
% 解答(章末)A3.2
右の図のように,立方体を$\mathrm{ABCD}-\mathrm{EFGH}$とし,各面の対角線の交点を頂点とする正八面体をPQRSTUとする. (1)辺$\mathrm{AB},\mathrm{BC}$の中点をそれぞれ$\mathrm{M},\mathrm{N}$とすると, $$ \mathrm{QR}=\mathrm{MN} =\sqrt{1^2+1^2} =\sqrt{2} $$ (2)PUは平面QRSTに垂直であり,四角錐$\mathrm{P}-\mathrm{QRST}$と四角錐$\mathrm{U}-\mathrm{QRST}$は合同であるから,求める正八面体の体積は, $$ \begin{aligned} 2 \times (\text{四角錐 P$-$QRST})& =2 \cdot\left\{\frac{1}{3} \cdot(\text {四角形 } \mathrm{QRST}) \cdot \frac{1}{2} \mathrm{PU}\right\} \\ & =2 \cdot \frac{1}{3} \cdot\left(\sqrt{2}\right)^2 \cdot 1 \\ & =\frac{4}{3} \end{aligned} $$
% 解答(章末)A3.3
正$m$面体($m$は$4$以上の自然数)の頂点の数を$v$,辺の数を$e$,面の数を$f$とする. 正$m$面体の1つの頂点に集まる角の和は$360^\circ$より小さく,1つの頂点には少なくとも3つ以上の面が集まる. したがって,1つの頂点に集まる面の数を$n$($n$は3以上の自然数)とすると, $$ 60^\circ \times n < 360^\circ $$ ゆえに,$n<6$であるから,$n = 3,4,5$の場合について考える. (i)$n = 3$のとき 1つの頂点に3つの面が集まるから, $$ v = \frac{3 \times m}{3} = m,e = \frac{3 \times m}{2} = \frac{3}{2} m,f = m $$ これらをオイラーの定理に代入すると, $$ m - \frac{3}{2} m + m = 2 $$ したがって,$m=4$であるから,この正多面体は正四面体である. (ii)$n = 4$のとき 1つの頂点に4つの面が集まるから, $$ v = \frac{3 \times m}{4} = \frac{3}{4} m,e = \frac{3 \times m}{2} = \frac{3}{2} m,f = m $$ これらをオイラーの定理に代入すると, $$ \frac{3}{4} m - \frac{3}{2} m + m = 2 m = 8 $$ したがって,$m=8$であるから,この正多面体は正八面体である. (iii)$n = 5$のとき 1つの頂点に5つの面が集まるから, $$ v = \frac{3 \times m}{5} = \frac{3}{5} m,e = \frac{3 \times m}{2} = \frac{3}{2} m,f = m $$ これらをオイラーの定理に代入すると, $$ \frac{3}{5} m - \frac{3}{2} m + m = 2 $$ したがって,$m=20$であるから,この正多面体は正二十面体である. よって,(i)〜(iii)より,各面が正三角形である正多面体は, 正四面体,正八面体,正二十面体の3種類ある.
% 解答(章末)A3.4
(1)線分$\mathrm{FP}$,線分$\mathrm{EA}$,線分$\mathrm{HQ}$の延長の交点をOとすると,$\mathrm{QA}:\mathrm{HE}=4:8=1:2$であるから, $\mathrm{OA}:\mathrm{OE}=1:2$ したがって,三角錐$\mathrm{OPQA}$と三角錐$\mathrm{OFHE}$の体積比は, $$ 1^3:2^3=1:8 $$ ここで,三角錐$\mathrm{OFHE}$の体積は, $$ \begin{aligned} \frac{1}{3} \cdot \triangle \mathrm{FHE} \cdot \mathrm{OE} & = \frac{1}{3} \cdot \left( \frac{1}{2} \cdot 8 \cdot 8 \right) \cdot 16 \\ & = \frac{1}{3} \cdot 32 \cdot 16 = \frac{512}{3} \end{aligned} $$ よって,求める体積は, $$ \frac{512}{3} \cdot \left( 1 - \frac{1}{8} \right) = \frac{512}{3} \cdot \frac{7}{8} = \frac{3584}{24} = \frac{448}{3} $$ (2)Oから$\mathrm{FH}$に垂線ORを下ろす.$\triangle \mathrm{OFH}$は二等辺三角形であるから,ORは$\mathrm{FH}$の垂直二等分線である. $\mathrm{FP} = \sqrt{8^2 + 4^2} = 4 \sqrt{5},\mathrm{FH} = \sqrt{8^2 + 8^2} = 8 \sqrt{2}$より,$\mathrm{FO} = 8 \sqrt{5},\mathrm{RH} = 4 \sqrt{2}$ したがって, $$ \mathrm{OR} = \sqrt{(8 \sqrt{5})^2 - (4 \sqrt{2})^2} = 12 \sqrt{2} $$ ゆえに, $$\triangle \mathrm{OFH} = \frac{1}{2} \cdot 8 \sqrt{2} \cdot 12 \sqrt{2} = \frac{1}{2} \cdot 192 = 96$$ ここで,$\triangle \mathrm{OPQ} \backsim \triangle \mathrm{OFH}$であり,$\mathrm{OP}:\mathrm{OF} = 1:2$より,$\triangle \mathrm{OPQ}$と$\triangle \mathrm{OFH}$の面積比は, $$ 1^2:2^2 = 1:4 $$ よって,台形$\mathrm{PQHF}$の面積は, $ 96 \cdot \left(1-\frac{1}{4} \right) = 96 \cdot \frac{3}{4} = 72$