% 例題A1.2.18：最短経路2 （One More）★★★
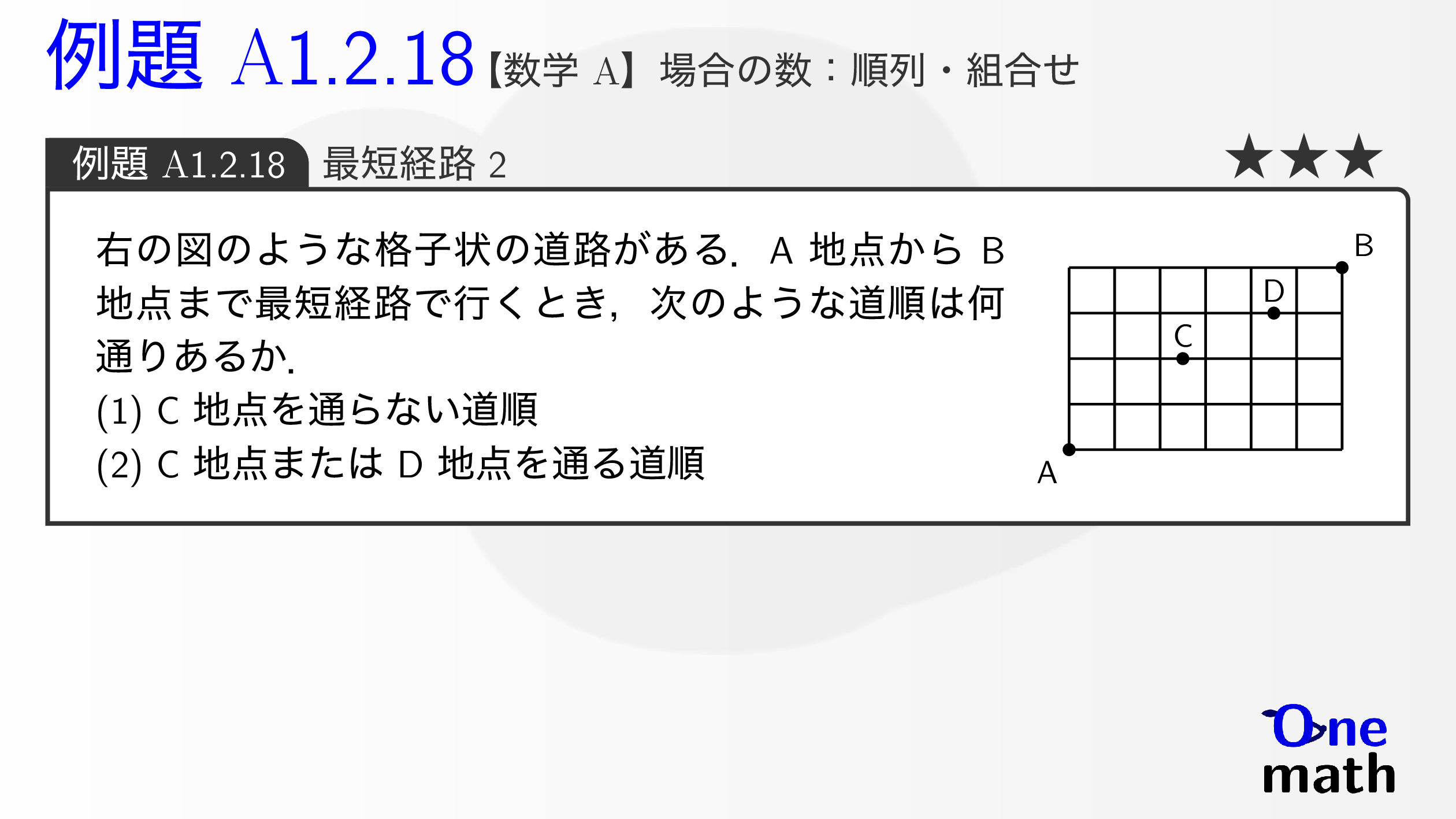
右の図のような格子状の道路がある.A地点からB地点まで最短経路で行くとき,次のような道順は何通りあるか. (1)C地点を通らない道順 (2)C地点またはD地点を通る道順
% 解答（例題A1.2.18）
(1)A地点からB地点へのすべての道順は,$\frac{10!}{6!4!}=210 (\text{通り})$C地点を通る道順は,$\frac{4!}{2!2!} \times\frac{5!}{3!2!}=60 (\text{通り})$よって,C地点を通らない道順は,$210-60=150(\text{通り})$(2)D地点を通る道順は,$\frac{7!}{4!3!} \times\frac{2!}{1!1!}=70(\text{通り})$C地点かつD地点を通る道順は,$$\frac{4!}{2!2!} \times\frac{2!}{1!1!}\times\frac{2!}{1!1!}=24(\text{{通り}})$$よって,(1)より,C地点を通る道順は60通りであるから,求める道順は,$$60+70-24=106(\text{通り})$$
% 問題A1.2.18
右の図のような格子状の道路がある.A地点からB地点まで最短経路で行くとき,次のような道順は何通りあるか. (1)C地点を通らない道順 (2)C地点またはD地点を通る道順
% 解答A1.2.18
(1)A地点からB地点へのすべての道順は,$\frac{10!}{5!5!}=252 (\text{通り})$C地点を通る道順は,$\frac{4!}{2!2!} \times\frac{5!}{2!3!}=60 (\text{通り})$よって,C地点を通らない道順は,$252-60=192(\text{通り})$(2)D地点を通る道順は,$\frac{6!}{3!3!} \times\frac{3!}{1!2!}=60(\text{通り})$C地点かつD地点を通る道順は,$$\frac{4!}{2!2!} \times 1 \times\frac{3!}{1!2!}=18(\text{{通り}})$$よって,(1)より,C地点を通る道順は60通りであるから,求める道順は,$$60+60-18=102(\text{通り})$$
