% 例題A1.2.17：最短経路1 （One More）★★
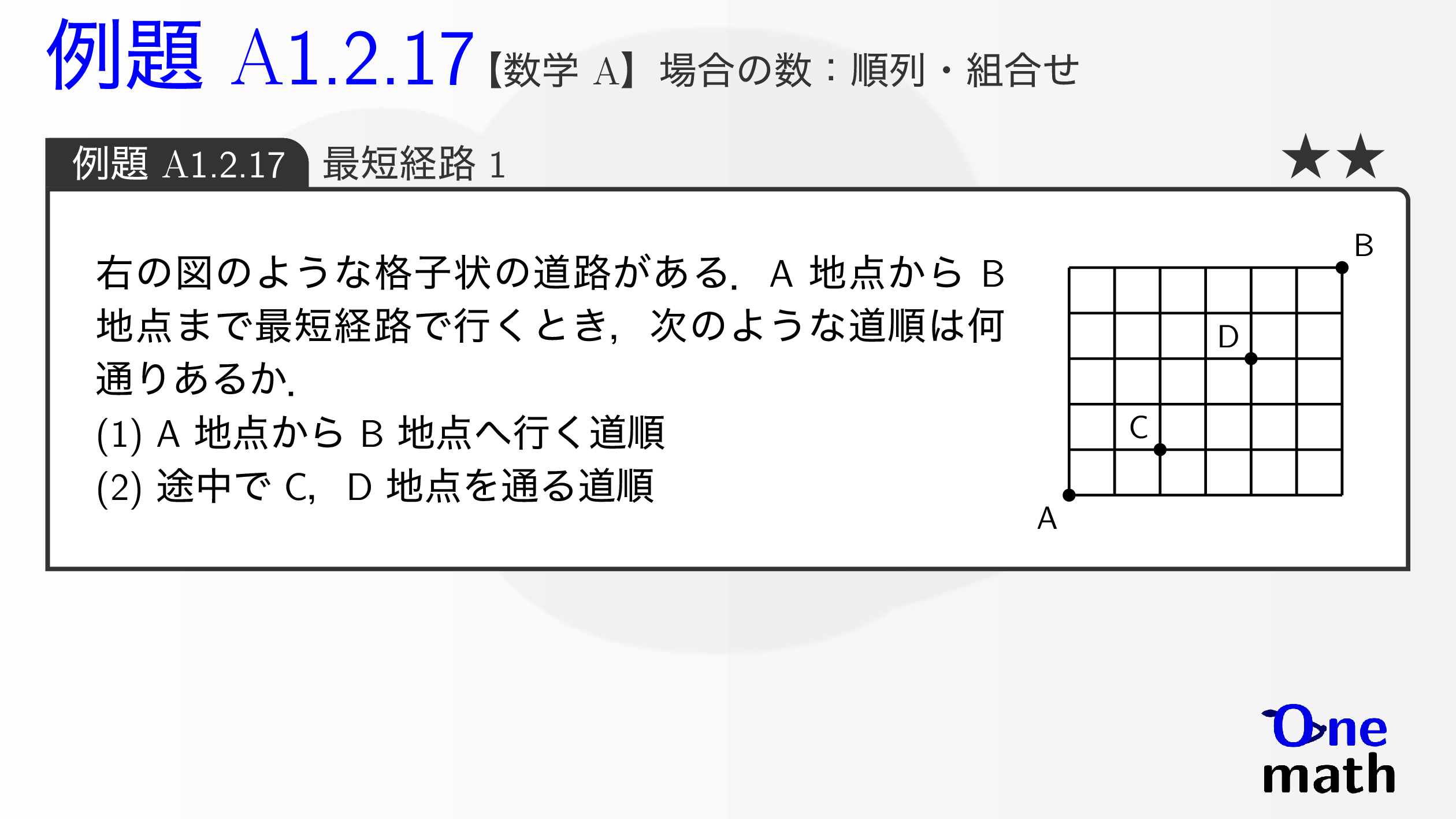
右の図のような格子状の道路がある.A地点からB地点まで最短経路で行くとき,次のような道順は何通りあるか. (1)A地点からB地点へ行く道順 (2)途中でC,D地点を通る道順
% 解答（例題A1.2.17）
A地点からB地点へは,右へ6区画,上へ5区画進む必要がある.右へ1区画進むことを$\rightarrow$,上へ1区画進むことを$\uparrow$と表すと,A地点からB地点へは6個の$\rightarrow$と5個の$\uparrow$の順列で表される. (1) A地点からB地点へは,6個の$\rightarrow$と5個の$\uparrow$の順列であるから,$$\frac{11!}{6!5!}=462(\text{通り})$$(2)A地点からC地点へは,右へ2区画,上へ1区画進めばよい. つまり,2個の$\rightarrow$と1個の$\uparrow$の順列であるから,$\frac{3!}{2!1!}=3(\text{通り})$C地点からD地点へは右へ2区画,上へ2区画進めばよい. つまり,2個の$\rightarrow$と2個の$\uparrow$の順列であるから,$\frac{4!}{2!2!}=6(\text{通り})$D地点からB地点へは右へ2区画,上へ2区画進めばよい. つまり,2個の$\rightarrow$と2個の$\uparrow$の順列であるから,$\frac{4!}{2!2!}=6(\text{通り})$よって,A地点からC,Dを経由してB地点まで行く道順は,$$3 \times 6 \times 6=108 (\text{通り})$$別解： (1)${ }_{11} \mathrm{C}_5=462(\text{通り})$(2)${ }_3 \mathrm{C}_1 \times { }_4 \mathrm{C}_2 \times { }_4 \mathrm{C}_2=3 \times 6 \times 6=108(\text{通り})$
% 問題A1.2.17
右の図のような格子状の道路がある.A地点からB地点まで最短経路で行くとき,次のような道順は何通りあるか. (1)A地点からB地点へ行く道順 (2)途中でC,D地点を通る道順 (3)途中でE地点を通る道順
% 解答A1.2.17
A地点からB地点へは,右へ7区画,上へ6区画進む必要がある.右へ1区画進むことを$\rightarrow$,上へ1区画進むことを$\uparrow$と表すと,A地点からB地点へは7個の$\rightarrow$と6個の$\uparrow$の順列で表される. (1) A地点からB地点へは,7個の$\rightarrow$と6個の$\uparrow$の順列であるから,$$\frac{13!}{7!6!}=1716(\text{通り})$$(2)A地点からC地点へは,右へ3区画,上へ2区画進めばよい. つまり,3個の$\rightarrow$と2個の$\uparrow$の順列であるから,$\frac{5!}{3!2!}=10(\text{通り})$C地点からD地点へは右へ2区画,上へ2区画進めばよい. つまり,2個の$\rightarrow$と2個の$\uparrow$の順列であるから,$\frac{4!}{2!2!}=6(\text{通り})$D地点からB地点へは右へ2区画,上へ2区画進めばよい. つまり,2個の$\rightarrow$と2個の$\uparrow$の順列であるから,$\frac{4!}{2!2!}=6(\text{通り})$よって,A地点からC,Dを経由してB地点まで行く道順は,$$10 \times 6 \times 6=360 (\text{通り})$$(3) 右の図のように,E地点の左隣りの地点をX地点,右隣りの地点をY地点とする. A地点からX地点へは,右へ3区画,上へ3区画進めばよい. つまり,3個の$\rightarrow$と3個の$\uparrow$の順列であるから,$\frac{6!}{3!3!}=20(\text{通り})$X地点からY地点まで行く道順は,1通り Y地点からB地点へは,右へ3区画,上へ3区画進めばよい. つまり,3個の$\rightarrow$と3個の$\uparrow$の順列であるから,$\frac{6!}{3!3!}=20(\text{通り})$よって,A地点からE地点を経由してB地点まで行く道順は,$$20 \times 1 \times 20=400 (\text{通り})$$別解： (1)${ }_{13} \mathrm{C}_6=1716(\text{通り})$(2)${ }_5 \mathrm{C}_2 \times { }_4 \mathrm{C}_2 \times { }_4 \mathrm{C}_2=10 \times 6 \times 6=360(\text{通り})$(3)${ }_6 \mathrm{C}_3 \times 1 \times { }_6 \mathrm{C}_3=20 \times 1 \times 20=400(\text{通り})$
