% 節末A1.1.1★★
ある町の住民の一部にアンケートを実施したところ,スポーツが好きと答えた住民は全体の$65 \%$,読書が好きと答えた住民は全体の$55 \%$,両方とも好きではないと答えた住民は全体の$15 \%$,さらに両方とも好きと答えた住民は$42$人であった.アンケートに答えた住民の総数を求めよ.また,スポーツだけが好きと答えた住民の人数を求めよ.
% 節末A1.1.2★★★
ある企業の社員140人を対象にアンケートを実施したところ,英語が得意な社員は110人,中国語が得意な社員は100人,スペイン語が得意な社員は90人であった.このとき,3言語すべてが得意な社員の人数は,少なくとも何人であるか.
% 節末A1.1.3★★★
50人の社員に対し,異なる3種類の技術A,B,Cを習得しているか調査したところ,全員がA,B,Cのうち少なくとも1つの技術を習得していた.また,AとBの両方,BとCの両方,AとCの両方を習得している社員の数はそれぞれ10人,8人,12人であった.さらに,AとBの少なくとも一方,BとCの少なくとも一方,AとCの少なくとも一方を習得している社員の数は,それぞれ40人,35人,45人であった.このとき,次の社員の人数を求めよ. (1)技術Aを習得している社員 (2)技術Bを習得している社員 (3)技術Cを習得している社員 (4)A,B,Cの全ての技術を習得している社員
% 節末A1.1.4★★
720の正の約数の個数は何個あるか.そのうち,奇数の約数は何個あるか.
% 節末A1.1.5★★★
赤玉3個,白玉2個,青玉1個,黄玉1個がある.この中から4個の玉を選ぶ方法は全部で何通りあるか.ただし,選ばれない色があってもよいものとする.
% 節末A1.2.1★★★
6個の数字$0,1,2,3,4,5$から異なる3個の数字を選んで3桁の整数を作る.このとき,次の問いに答えよ. (1)偶数の個数を求めよ. (2)234以上の整数の個数を求めよ. (3)これらを小さい順に並べたとき,第45番目にある整数を求めよ.
% 節末A1.2.2★★★
大人4人,子供3人がいるとするとき,次の並び方は何通りあるか. (1)子供のうち2人だけが隣り合うように7人を1列に並べる. (2)子供の両隣りが必ず大人になるように7人を円形に並べる.
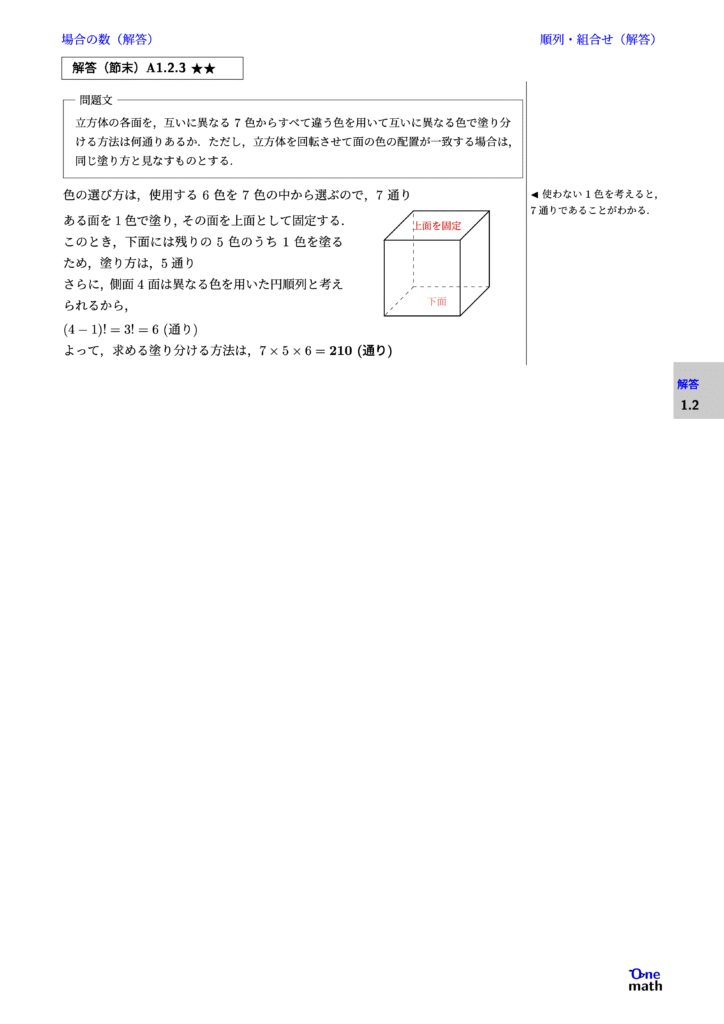
% 節末A1.2.3★★
立方体の各面を,互いに異なる7色からすべて違う色を用いて互いに異なる色で塗り分ける方法は何通りあるか.ただし,立方体を回転させて面の色の配置が一致する場合は,同じ塗り方と見なすものとする.
% 節末A1.2.4★★★
(1)全部で何通りの並び方があるか. (2)Sが3つ連続する並び方は何通りあるか. (3)Sが2つ以上連続する並び方は何通りあるか. (4)Sが2つ以上連続し,かつ,Cも2つ連続する並び方は何通りあるか.
% 節末A1.2.5★★★★
右の図のような格子状の道路がある.次のような場合に,道順は何通りあるか.ただし,東方向,北方向,北東方向にしか進めないものとする. (1)A地点からC地点へ行く道順 (2)A地点からC地点を通らないでB地点へ行く道順
% 章末A1.1★★
分母が200であり,分子が1から200までの200個の分数のうち,約分できないものの個数を求めよ.
% 章末A1.2★★★
区別のつかない7個のボールを区別のつかない3つの箱に入れる.1個も入らない箱があってもよい場合,ボールの入れ方は全部で何通りあるか.
% 章末A1.3★★★
次の等式を満たす自然数$n$の値を求めよ. (1)${ }_n \mathrm{P}_3=2{ }_n \mathrm{P}_2+10 { }_n \mathrm{P}_1$ (2)$2{ }_n \mathrm{C}_4=5{}_n \mathrm{C}_3$
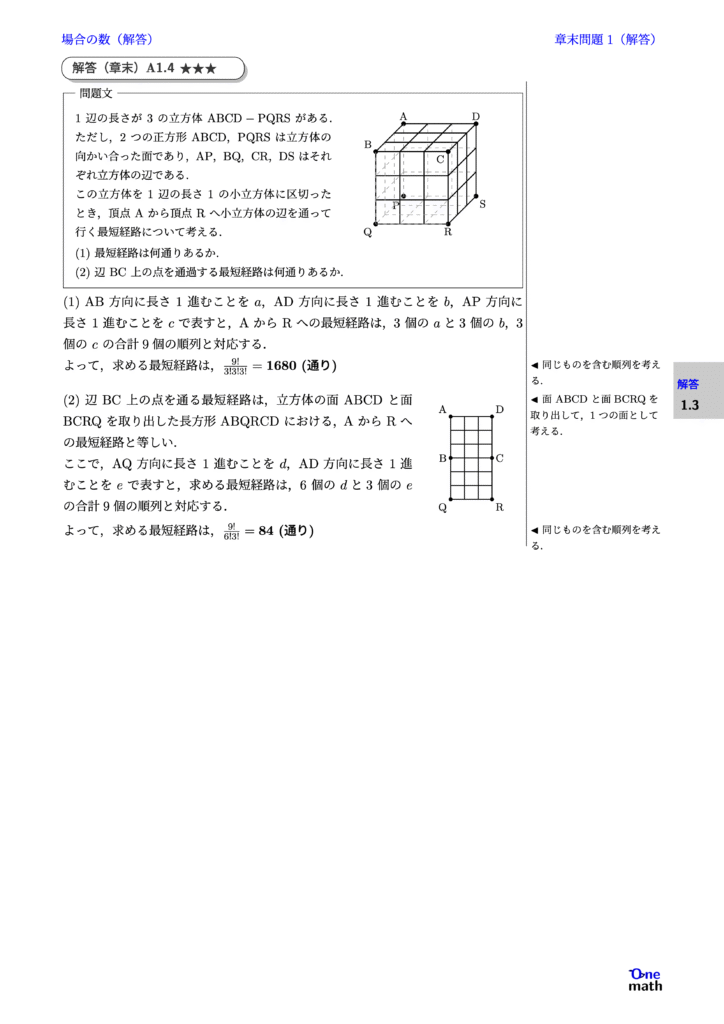
% 章末A1.4★★★
1辺の長さが3の立方体$\mathrm{ABCD}-\mathrm{PQRS}$がある.ただし,2つの正方形ABCD,PQRSは立方体の向かい合った面であり,AP,BQ,CR,DSはそれぞれ立方体の辺である. この立方体を1辺の長さ1の小立方体に区切ったとき,頂点Aから頂点Rへ小立方体の辺を通って行く最短経路について考える. (1)最短経路は何通りあるか. (2)辺BC上の点を通過する最短経路は何通りあるか.
% 章末A1.5★★★★
サイコロを4回投げて,$k$回目に出た目を$a_k$とする.このとき,$a_1 \leqq a_2 < a_3 \leqq a_4$となる目の出方は何通りあるか.
% 解答（節末）A1.1.1
アンケートに答えた住民全体の集合を$U$, スポーツが好きと答えた住民の集合を$A$, 読書が好きと答えた住民の集合を$B$とする. $n(U)=x$とおくと, $$ n(A)=0 .65 x,n(B)=0 .55 x,n(\overline{A} \cap \overline{B})=0 .15 x,n(A \cap B)=42 $$ $n(\overline{A} \cap \overline{B})=n(\overline{A \cup B})=n(U)-n(A \cup B)$であるから, $$ n(A \cup B)=n(U)-n(\overline{A} \cap \overline{B})=x-0 .15 x=0 .85 x\cdots(\mathrm{i}) $$ また, $$ n(A \cup B) =n(A)+n(B)-n(A \cap B)=0 .65 x+0 .55 x-42=1 .2 x-42 \cdots(\mathrm{ii}) $$ (i),(ii)より, $ 0 .85 x=1 .2 x-42 $ したがって,$x=120$ よって,アンケートに答えた住民は$120$人 また,スポーツだけが好きと答えた住民の人数は$n(A)-n(A \cap B)$であるから, $$ n(A)-n(A \cap B)=0 .65 x-42=0 .65 \times 120-42=36 \text{ (人) } $$
% 解答（節末）A1.1.2
140人の社員全体の集合を$U$,英語,中国語,スペイン語が得意な社員の集合をそれぞれ$A,B,C$とする. また,英語と中国語のみ,中国語とスペイン語のみ,スペイン語と英語のみに得意な社員をそれぞれ$x$人,$y$人,$z$人,3言語すべてが得意な社員を$w$人とする. 社員全体について, $$ 110+100+90-(x+w)-(y+w)-(z+w)+w \leqq 140 $$ すなわち, $$ 160-(x+y+z)-2 w \leqq 0\cdots(\mathrm{i}) $$ 集合$A$,$B$,$C$のそれぞれについて, $$ 110 \geqq x+z+w\cdots(\mathrm{ii}), 100 \geqq x+y+w\cdots(\mathrm{iii}),90 \geqq y+z+w\cdots(\mathrm{iv})$$ (ii)〜(iv)の辺々を足し合わせると, $$ 300 \geqq 2(x+y+z)+3 w $$ すなわち,$ 2(x+y+z)+3 w-300 \leqq 0\cdots(\mathrm{v})$ (v)と(i)$\times 2$の辺々を足し合わせると,$20-w \leqq 0$ したがって,$w \geqq 20$ また,$w=20$のとき,(i)〜(iv)の不等号を等号におき換えた連立方程式は,負ではない整数解$(x,y,z)=(50,30,40)$をもつ. よって,3言語すべてが得意な社員の人数は,少なくとも$20$人
% 解答（節末）A1.1.3
技術A,B,Cを習得している社員の集合をそれぞれ$A,B,C$とすると, $$ n(A \cup B \cup C)=50,n(A \cap B)=10,n(B \cap C)=8,n(C \cap A)=12, $$ $$ n(A \cup B)=40,n(B \cup C)=35,n(C \cup A)=45 $$ $n(A \cup B)=n(A)+n(B)-n(A \cap B)$より,$n(A)+n(B)=50 \cdots(\mathrm{i})$ $n(B \cup C)=n(B)+n(C)-n(B \cap C)$より,$n(B)+n(C)=43 \cdots(\mathrm{ii})$ $n(C \cup A)=n(C)+n(A)-n(C \cap A)$より,$n(C)+n(A)=57 \cdots(\mathrm{iii})$ (i)〜(iii)の辺々を足し合わせると, $$ n(A)+n(B)+n(C)=75\cdots(\mathrm{iv}) $$ (1)$(\mathrm{iv})-(\mathrm{ii})$より,$n(A)= 32 (\text{人}) $ (2)$(\mathrm{iv})-(\mathrm{iii})$より,$n(B)= 18 (\text{人}) $ (3)$(\mathrm{iv})-(\mathrm{i})$より,$n(C)=25 (\text{人}) $ (4)全ての技術を習得している社員の数を求めると, $$ \begin{aligned} n(A \cup B \cup C)=n(A) & +n(B)+n(C)-n(A \cap B) \\ & -n(B \cap C)-n(C \cap A)+n(A \cap B \cap C) \end{aligned} $$ であるから, $ n(A \cap B \cap C)=50-32-18-25+10+8+12=5 (\text{人}) $
% 解答（節末）A1.1.4
720を素因数分解すると,$720=2^4 \times 3^2 \times 5$ $$ (4+1) \times(2+1) \times(1+1)=30 $$ より,約数の個数は,30個 奇数の約数は,$3^2 \times 5$の約数であるから, $$ (2+1) \times(1+1)=6 $$ より,奇数の約数の個数は,6個
% 解答（節末）A1.1.5
選んだ4個の玉に含まれる赤玉,白玉,青玉,黄玉の個数をそれぞれ$a,b,c,d$とし,$(a,b,c,d)$で表す. $0 \leqq a \leqq 3$であるから,4個の玉を選ぶ方法は次の4つの場合がある. (i)$a=3$のとき 赤玉を3個選び,残りの1個を他の色から選ぶので, $$ (a,b,c,d)=(3,1,0,0),(3,0,1,0),(3,0,0,1) $$ の3通り (ii)$a=2$のとき 赤玉を2個選び,残りの2個を他の色から選ぶので, $$ (a,b,c,d)=(2,2,0,0),(2,1,1,0),(2,1,0,1),(2,0,1,1) $$ の4通り (iii)$a=1$のとき 赤玉を1個選び,残りの3個を他の色から選ぶので, $$ (a,b,c,d)=(1,2,1,0),(1,2,0,1),(1,1,1,1) $$ の3通り (iv)$a=0$のとき 赤玉を選ばず,残りの4個を他の色から選ぶので, $$ (a,b,c,d)=(0,2,1,1) $$ の1通り よって,(i)〜(iv)は同時に起こらないから,$ 3+4+3+1=11 (\text{通り}) $
% 解答（節末）A1.2.1
(1) (i)一の位が$0$ 百,十の位に残りの5個の数字から2個選んで並べればよいので,その個数は, $ { }_5 \mathrm{P}_2 = 5 \cdot 4 = 20 (\text{個})$ (ii)一の位が$2$または$4$のとき 一の位は2,4の2通りあり,そのそれぞれについて, 百の位は$0$以外で一の位の数を除く$4$通りある. 十の位は百の位と一の位の数以外の$4$通りあるから, その個数は, $ 4 \times 4 \times 2 = 32 (\text{個}) $ よって,(i),(ii)より,求める個数は, $ 20 + 32 = 52 (\text{個}) $ (2) (i)百の位が$2$,十の位が$3$のとき 一の位は$4,5$の$2$通り (ii)百の位が$2$,十の位が$4,5$のとき 一の位は$4$通りずつあるから, $ 2 \times 4 = 8 (\text{個}) $ (iii)百の位が$3,4,5$のとき 残りの位は${ }_5 \mathrm{P}_2$通りずつあるから, $$ 3 \times { }_5 \mathrm{P}_2 = 3 \times 5 \cdot 4 = 60 (\text{個}) $$ よって,(i)〜(iii)より,求める個数は, $ 2 + 8 + 60 = 70 (\text{個})$ (3)百の位が$1$である整数は,${ }_5 \mathrm{P}_2 = 5 \cdot 4 = 20 (\text{個})$ 百の位が$2$である整数も同様に,$20 (\text{個})$ したがって,第$45$番目にある整数は,百の位が$3$である整数のうち,小さいものから$5$番目の整数である. 百の位が$3$,十の位が$0$のものが$4$個あるので,$310$が第$45$番目となる. よって,求める整数は,$310$
% 解答（節末）A1.2.2
(1)すべての場合から,「子供3人が隣り合う場合」と「子供が隣り合わない場合」を引けばよい. 7人の並び方は, $ 7! = 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 5040 (\text{通り}) $ 子供3人が隣り合うような並び方は, $$ 5! \times 3! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \times 3 \cdot 2 \cdot 1 = 720 (\text{通り}) $$ 子供が隣り合わない並び方は,大人4人の間と両端の5箇所のうち,3箇所に子供3人が1人ずつ入ればよい. 大人の並び方は, $ 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 (\text{通り}) $ 子供3人の並び方は,5箇所から3箇所選んで並べる順列であるから, $$ {}_5 \mathrm{P}_3 = 5 \cdot 4 \cdot 3 = 60 (\text{通り}) $$ したがって, $ 24 \times 60 = 1440 (\text{通り}) $ よって,求める並び方は, $ 5040 - (720 + 1440) = 2880 (\text{通り}) $ 別解： 大人4人の間と両端の5箇所のうち,2箇所に子供2人の組と残りの子供1人が入ればよい. 大人の並び方は, $ 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 (\text{通り}) $ 子供2人の組と子供1人が入る場所の選び方は,5箇所から2箇所選んで並べる順列であるから, $$ {}_5 \mathrm{P}_2 = 5 \cdot 4 = 20 (\text{通り}) $$ 子供の並び方は, $ 3! = 3 \cdot 2 \cdot 1 = 6 (\text{通り}) $ よって,求める並び方は,$ 24 \times 20 \times 6 = 2880 (\text{通り}) $ (2)円周上に大人4人が並ぶ並び方は, $ (4-1)! = 3! = 3 \cdot 2 \cdot 1 = 6 (\text{通り}) $ 大人と大人の間の4箇所に子供3人が1人ずつ入ればよいから, $$ {}_4 \mathrm{P}_3 = 4 \cdot 3 \cdot 2 = 24 (\text{通り}) $$ よって,求める並び方は, $ 6 \times 24 = 144 (\text{通り}) $
% 解答（節末）A1.2.3
色の選び方は,使用する6色を7色の中から選ぶので, $7$ 通り ある面を1色で塗り,その面を上面として固定する. このとき,下面には残りの5色のうち1色を塗るため,塗り方は,5通り さらに,側面4面は異なる色を用いた円順列と考えられるから, $ (4-1)! = 3! = 6 (\text{通り}) $ よって,求める塗り分ける方法は, $ 7 \times 5 \times 6 = 210 (\text{通り}) $
% 解答（節末）A1.2.4
(1)3個のSと2個のCと,U,Eをそれぞれ1個ずつ含む7個の順列であるから, $$ \frac{7!}{3!2!} = 420 (\text{通り}) $$ (2)SSSをひとまとまりにして1つの文字として考えて, $ \frac{5!}{2!} = 60 (\text{通り}) $ (3)Sが連続しない並び方を考える.C,C,U,Eを並べると,$\frac{4!}{2!} = 12 (\text{通り})$ これらの4文字の間と両端の5箇所のうち,3箇所にSを並べる並び方は,${}_5\mathrm{C}_3$通り したがって,Sが続かない並び方は, $ 12 \times {}_5\mathrm{C}_3 = 12 \times 10 = 120 (\text{通り}) $ よって,求める並び方は, $ 420 - 120 = 300 (\text{通り}) $ (4)CCが連続する場合の並び方は,CCをひとまとまりにして1つの文字として考えて, $$ \frac{6!}{3!} = 120 (\text{通り}) $$ そのうち,Sが連続しないものは,CC,U,Eを並べ,これらの間と両端の4箇所のうち,3箇所にSを並べるから, $$ 3! \times {}_4\mathrm{C}_3 = 24 (\text{通り}) $$ よって,求める並び方は, $ 120 - 24 = 96 (\text{通り}) $
% 解答（節末）A1.2.5
東へ1区画進むことを$\rightarrow$,北へ1区画進むことを$\uparrow$,北東へ1区画進むことを$\nearrow$と表す. (1) (i)$\rightarrow$に2回,$\uparrow$に2回進むとき,2個の$\rightarrow$と2個の$\uparrow$の順列であるから, $ \frac{4!}{2!2!}=6 (\text{通り}) $ (ii)$\nearrow$に1回,$\rightarrow$に1回,$\uparrow$に1回進むとき,$\rightarrow$,$\nearrow$,$\rightarrow$の順列であるから, $ 3!=6 (\text{通り}) $ (iii)$\nearrow$に2回進むとき,1通り よって,(i)〜(iii)より,求める道順は, $6+6+1=13 (\text{通り}) $ (2)全体から,Cを通るものを引くことを考える.A地点からB地点へのすべての道順は, (i)$\rightarrow$に4回,$\uparrow$に4回進むとき,4個の$\rightarrow$と4個の$\uparrow$の順列であるから, $ \frac{8!}{4!4!}=70 (\text{通り}) $ (ii)$\rightarrow$に1回,$\uparrow$に3回,$\nearrow$に3回進むとき,1個の$\rightarrow$と3個の$\uparrow$と3個の$\nearrow$の順列であるから, $ \frac{7!}{1!3!3!}=140 (\text{通り}) $ (iii)$\rightarrow$に2回,$\uparrow$に2回,$\nearrow$に2回進むとき,2個の$\rightarrow$と2個の$\uparrow$と2個の$\nearrow$の順列であるから, $ \frac{6!}{2!2!2!}=90 (\text{通り}) $ (iv)$\rightarrow$に3回,$\uparrow$に1回,$\nearrow$に1回進むとき,3個の$\rightarrow$と1個の$\uparrow$と1個の$\nearrow$の順列であるから, $ \frac{5!}{3!1!1!}=20 (\text{通り}) $ (v)$\nearrow$に4回進むとき,1通り したがって,(i)〜(v)より,$70+140+90+20+1=321 (\text{通り})$ C地点からB地点への道順は,(1)と同様に考えると,13通り これと(1)より,A地点からC地点を通りB地点へ行く道順は,$$13\times 13=169 (\text{通り})$$ よって,求める道順は,$321-169=152 (\text{通り})$
% 解答（章末）A1.1
分母の200を素因数分解すると,$200=2^3 \cdot 5^2$ したがって,1から200までの整数のうち,2または5で割り切れないものの個数を求めればよい. 1から200までの整数全体の集合を$U$とすると,$ n(U)=200$ $U$の部分集合のうち,2の倍数全体の集合を$A$,5の倍数全体の集合を$B$とすると, $200=2 \cdot 100,200=5 \cdot 40$であるから, $$ n(A)=100,n(B)=40 $$ また,$A \cap B$は10の倍数全体の集合で,$200=10 \cdot 20$であるから, $ n(A \cap B)=20 $ したがって,$A \cup B$の個数は, $$ n(A \cup B) =n(A)+n(B)-n(A \cap B) =100+40-20=120 $$ よって,求める個数は, $ n(\overline{A \cup B}) =n(U)-n(A \cup B) =200-120=80 $
% 解答（章末）A1.2
3つの箱に入れるボールの個数を$x,y,z (x \leqq y \leqq z)$とする. ボールの入れ方は次の4つの場合があり,$x + y + z = 7$を満たす0以上の整数$x,y,z$の組の総数を求める. (i)$x = 0$のとき $y + z = 7 (0 \leqq y \leqq z)$より, $(y,z) = (0,7),(1,6),(2,5),(3,4)$の4組 (ii)$x = 1$のとき $y + z = 6 (1 \leqq y \leqq z)$より, $(y,z) = (1,5),(2,4),(3,3)$の3組 (iii)$x = 2$のとき $y + z = 5 (2 \leqq y \leqq z)$より, $(y,z) = (2,3)$の1組 (iv)$x \geqq 3$のとき $x + y + z = 7 (3 \leqq x \leqq y \leqq z)$より,このような$x,y,z$の組は存在しない. したがって,(i)〜(iv)より,$x,y,z$の組は, $ 4 + 3 + 1 = 8 (\text{組}) $ よって,ボールの入れ方は全部で,$8$通り
% 解答（章末）A1.3
(1)${ }_n \mathrm{P}_3=n(n-1)(n-2),{ }_n \mathrm{P}_2=n(n-1),{ }_n \mathrm{P}_1=n$ であるから, $$n(n-1)(n-2)=2n(n-1)+10 n$$ これを整理すると, $ n(n-6)(n+1)=0 $ よって,$n \geqq 3$であるから,$n=6$ (2)${ }_n \mathrm{C}_4=\frac{n(n-1)(n-2)(n-3)}{4 \cdot 3 \cdot 2 \cdot 1},{ }_n \mathrm{C}_3=\frac{n(n-1)(n-2)}{3 \cdot 2 \cdot 1}$であるから, $$ 2 \cdot \frac{n(n-1)(n-2)(n-3)}{4 \cdot 3 \cdot 2 \cdot 1}=5 \cdot \frac{n(n-1)(n-2)}{3 \cdot 2 \cdot 1} $$ したがって,$n(n-1)(n-2)(n-3)=10n(n-1)(n-2)$ これを整理すると, $ n(n-1)(n-2)(n-13)=0 $ $n \geqq 4$であるから,$n=13$
% 解答（章末）A1.4
(1)AB方向に長さ1進むことを$a$,AD方向に長さ1進むことを$b$,AP方向に長さ1進むことを$c$で表すと,AからRへの最短経路は,3個の$a$と3個の$b$,3個の$c$の合計9個の順列と対応する. よって,求める最短経路は, $ \frac{9!}{3!3!3!}= 1680 (\text{通り}) $ (2)辺BC上の点を通る最短経路は,立方体の面ABCDと面BCRQを取り出した長方形$\mathrm{ABQRCD}$における,AからRへの最短経路と等しい. ここで,AQ方向に長さ1進むことを$d$,AD方向に長さ1進むことを$e$で表すと,求める最短経路は,6個の$d$と3個の$e$の合計9個の順列と対応する. よって,求める最短経路は, $ \frac{9!}{6!3!} = 84 (\text{通り}) $
% 解答（章末）A1.5
$$\begin{array}{ll} (\mathrm{i}) a_1<a_2<a_3<a_4,& (\mathrm{ii}) a_1=a_2<a_3<a_4,\\ (\mathrm{iii}) a_1<a_2<a_3=a_4,& (\mathrm{iv}) a_1=a_2<a_3=a_4 \end{array}$$ の4つの場合に分けて考える. (i)$a_1<a_2<a_3<a_4$となるとき 6個のサイコロの目から異なる4個を選ぶ場合の数は, $$ { }_6 \mathrm{C}_4 = 15 (\text{通り}) $$ (ii)$a_1=a_2<a_3<a_4$となるとき 6個のサイコロの目から異なる3個を選ぶ場合の数は, $$ { }_6 \mathrm{C}_3 = 20 (\text{通り}) $$ (iii)$a_1<a_2<a_3=a_4$となるとき (ii)と同様に考えると, $ 20 (\text{通り}) $ (iv)$a_1=a_2<a_3=a_4$となるとき 6個のサイコロの目から異なる2個を選ぶ場合の数は, $$ { }_6 \mathrm{C}_2 = 15 (\text{通り}) $$ よって,(i)〜(iv)より,求める出方の総数は, $$ 15 + 20 + 20 + 15 = 70 (\text{通り}) $$ 別解： $b_1=a_1,b_2=a_2+1,b_3=a_3+1,b_4=a_4+2$とおくと, $a_1 \leqq a_2<a_3 \leqq a_4,1 \leqq a_i \leqq 6 (i=1,\ldots,4)$を満たす$\left(a_1,a_2,a_3,a_4\right)$ と, $b_1<b_2<b_3<b_4,1 \leqq b_i \leqq 8 (i=1,\ldots,4)$を満たす$\left(b_1,b_2,b_3,b_4\right)$ とは1対1に対応する. よって,これを満たす$\left(b_1,b_2,b_3,b_4\right)$の個数は,${ }_8 \mathrm{C}_4=70 (\text{通り})$
